載人深潛器鈦合金耐壓球殼極限強度可靠性分析

，

(上海交通大學 海洋工程國家重點實驗室，上海 200240)

目前全國產化的4 500 m載人深潛器正在研制中，將初步形成4 500 m水深的綜合探查和作業能力。載人深潛器的耐壓殼是保證潛水器正常工作和人員生命安全的重要結構構件，其設計的優劣直接關系到深潛器工作安全性和總體性能。對于工作深度大于800 m的載人潛水器，耐壓殼基本采用球形結構[1]。目前大深度載人潛水器的耐壓殼材料多選用鈦合金，具有較高的比強度，并且在海水中抗腐蝕能力強。耐壓球殼結構的極限強度和可靠性是評價深潛器安全性的重要指標，相關研究較多[2-6]。整體來看，國內外關于球殼極限強度的研究已有了一定的成果，但絕大多數局限于開孔或缺陷單獨作用時的球殼極限強度，沒有分析開孔、初始缺陷共同影響下極限強度的分布規律，也沒有明確地給出可以用于工程設計參考的開孔球殼極限強度計算公式，并且分析中選取的變量較少、范圍較小。為此，以全國產化4 500 m載人深潛器的研制為背景，結合國外載人深潛器下潛數據的統計資料，利用響應面方法對鈦合金球殼的結構可靠性進行計算，分析了各隨機變量的靈敏度。

1 鈦合金耐壓球殼極限強度的擬合

鈦合金耐壓球殼極限強度可靠性分析的關鍵之一在于獲得耐壓殼結構極限強度的表達式。完整球殼極限強度的經典理論公式適用于不考慮初始缺陷的情況，當需要考慮初始缺陷時，可采用數值分析方法將經典理論公式作為原型進行擬合。而實際耐壓殼上存在開孔，則可進一步將完整球殼的擬合公式作為原型，擬合出考慮初始缺陷的開孔耐壓球殼的極限強度表達式。

1.1 含初缺陷完整球殼極限強度的擬合公式

不考慮初始缺陷的球殼極限強度考慮的變量主要有球殼內半徑R、厚度t，材料屈服強度σy，其經典公式為

(1)

式中:R——球殼內半徑;

t——球殼厚度;

σy——材料的屈服強度。

根據計算，有限元計算結果與上述經典公式的計算結果之間保持線性關系，因此可以采用下式來表示完整球殼的極限強度。

(2)

初始缺陷有多種形式，為了簡化分析，采用文獻[4]中的缺陷模擬方法，考慮一階彈性屈曲模態下的缺陷，見圖1。

這種屈曲模態缺陷引入方式反映了最容易出現結構穩定性失效的形式，其中只需要初始缺陷幅值的一個參數即可表示整體缺陷情況，使分析更為快捷方便。

由于缺陷幅值Δ沿球殼徑向分布，其與球殼中面半徑的比值能夠反映出缺陷相對于球殼的大小。此外，缺陷幅值的增加會引起球殼極限強度的降低，因此以上述完整球殼極限強度公式為原型進行修改，含初始缺陷幅值Δ的完整球殼極限強度基本表達式可以寫成如下形式。

圖1 初始缺陷示意

(3)

式中：a、b、c——待定系數;

Δ——初始缺陷幅值。

1.2 含初始缺陷開孔球殼極限強度的擬合公式

開孔球殼有多種結構形式，其開孔在一定程度上會對結構的極限承載能力產生影響。開孔球殼主要考慮的基本參數有開孔孔徑Dk，開孔寬度bk，開孔加強處寬度bs，開孔連接處夾角θ、以及球殼厚度、內半徑等，開孔處的封閉則以開孔處厚度tk來等效，見圖2。

圖2 開孔球殼結構示意

一般來說，潛水器耐壓球殼開孔內徑Dk以及開孔寬度bk都是由耐壓球殼的布置要求確定的，因此在擬合公式中，不考慮這兩項的變化，但在擬合公式的系數確定過程中，包含這兩項的具體影響。

開孔連接處轉角θ在耐壓球殼設計過程中是一個重要的參數。為了分析θ對球殼極限強度的影響，保持球殼的半徑、厚度、材料屈服強度不變，僅改變轉角θ的大小。計算結果表明θ與極限強度之間基本呈線性關系，所以可以在完整球殼極限強度公式的基礎上增加轉角的線性項，表示轉角對極限強度的影響。考慮開孔結構參數的影響，可以得到擬合公式：

(4)

如果進一步考慮初始缺陷的影響，則同樣可以參考完整球殼極限強度的擬合公式(2)，得到開孔球殼的極限強度擬合公式：

(5)

以上各式中a、b、c、d均為待定系數。

2 4 500 m HOV鈦合金耐壓殼的極限狀態方程

2.1 極限強度表達式

分析對象為全國產4 500 m載人深潛器鈦合金耐壓球殼，該裝置屬于多開孔結構，設置了人員貨物出入艙口、觀察窗窗座等。球殼共有4個開孔，本文主要分析單開孔對球殼極限強度的影響，即分析開孔最大的人員出入孔。球殼開孔處內徑Dk=480 mm，球殼開孔處寬度bk=60 mm，開孔處厚度tk為140 mm，主要考慮開孔加強處寬度、球殼開孔連接處轉角、球殼內半徑、球殼厚度等對結構極限強度的影響。球殼內半徑考慮范圍為950～1 050 mm，球殼厚度考慮范圍為45～55 mm，加強處寬度考慮范圍為100～200 mm，球殼開孔連接處轉角范圍為2.55～2.90 rad，初始缺陷范圍為0～4 mm。

采用有限元方法計算含初始缺陷耐壓球殼的極限強度，模型見圖3。通過對模型計算時間和結果精度的綜合考慮，有限元單元尺寸取為50 mm大小。

圖3 開孔球殼有限元模型示意

4 500 m載人深潛器耐壓球殼所采用的鈦合金材料的彈性模量為115 GPa，泊松比為0.3，塑性本構關系見表1。

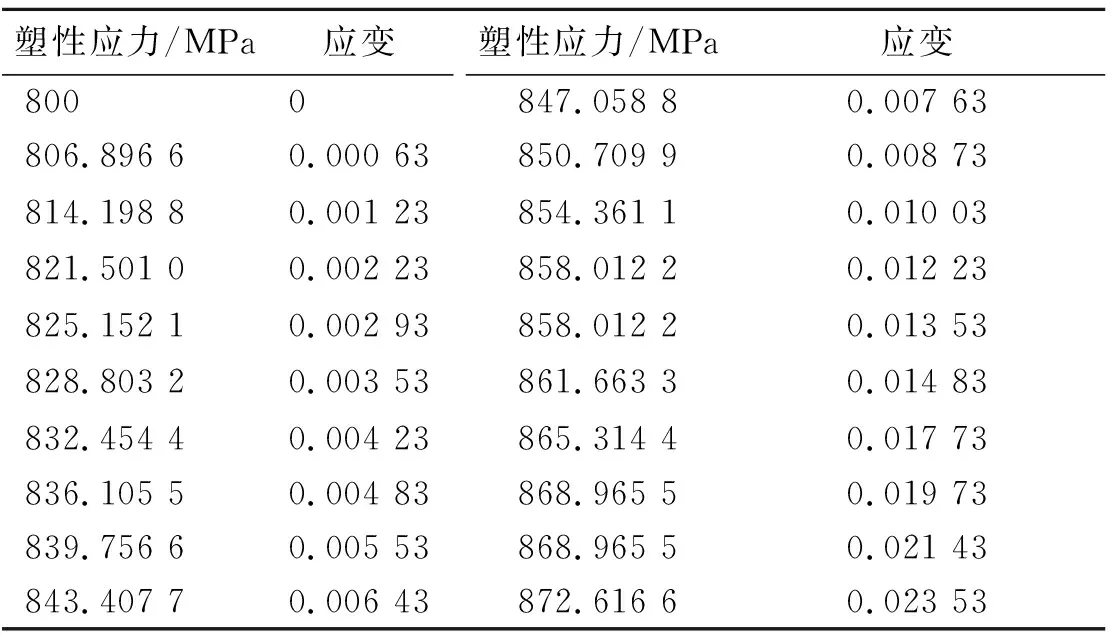
表1 鈦合金材料塑性本構關系

通過批量的有限元計算之后，獲得相應的計算結果(見圖4、5)。利用擬合公式(5)進行擬合，最終得到含初缺陷開孔球殼的極限強度表達式為

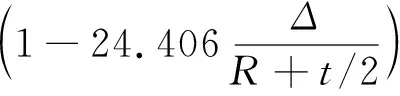
(6)

經檢驗，相關系數R為0.995 2，相關系數平方和為0.990 4，決定系數DC為0.990 4，擬合的相關程度很高。

2.2 極限狀態方程

對于載人深潛器耐壓球殼可以建立如下抗力-載荷效應模型的極限狀態方程：

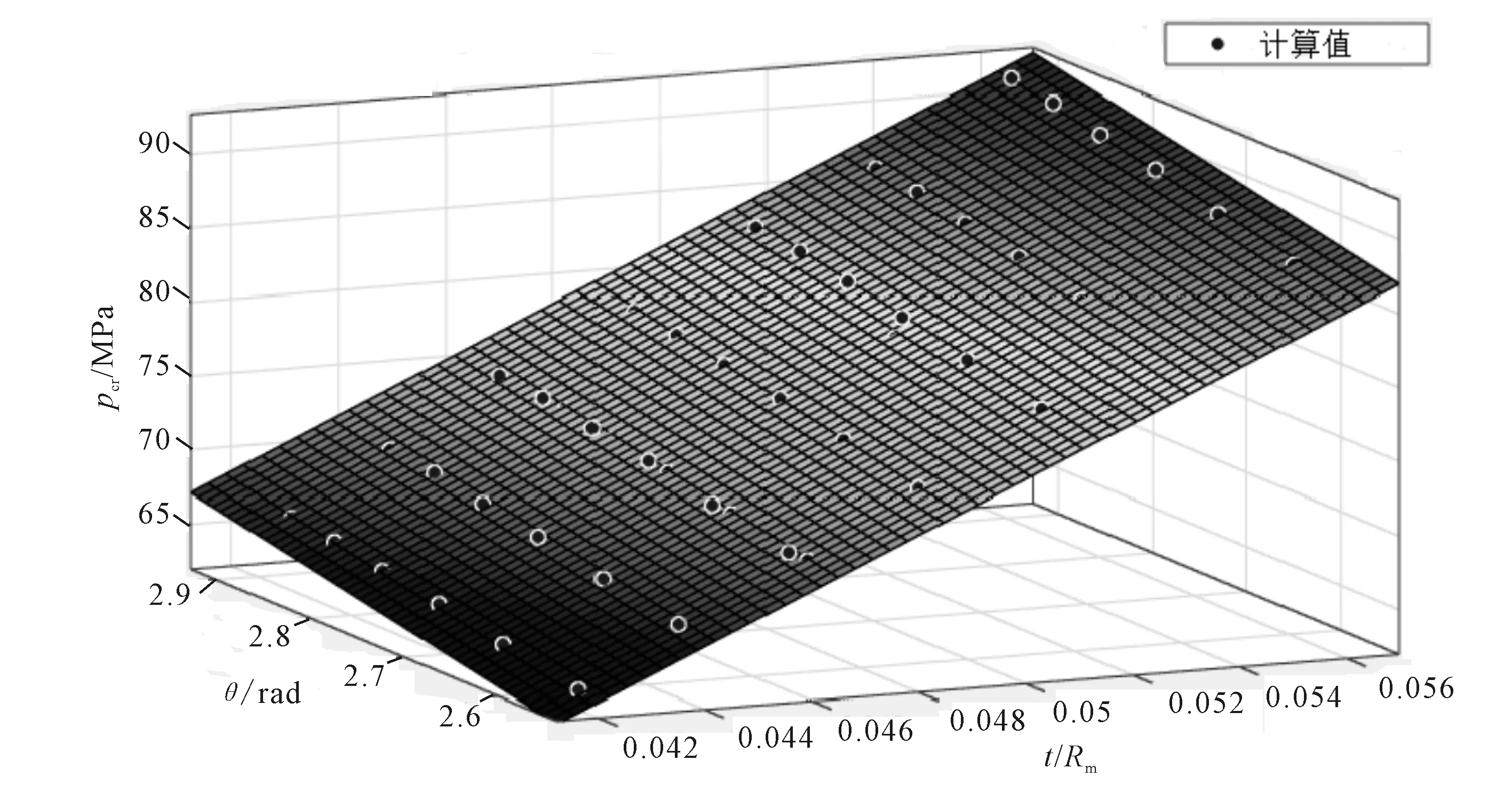
圖4 開孔球殼厚度半徑比、開孔連接夾角與極限強度間關系

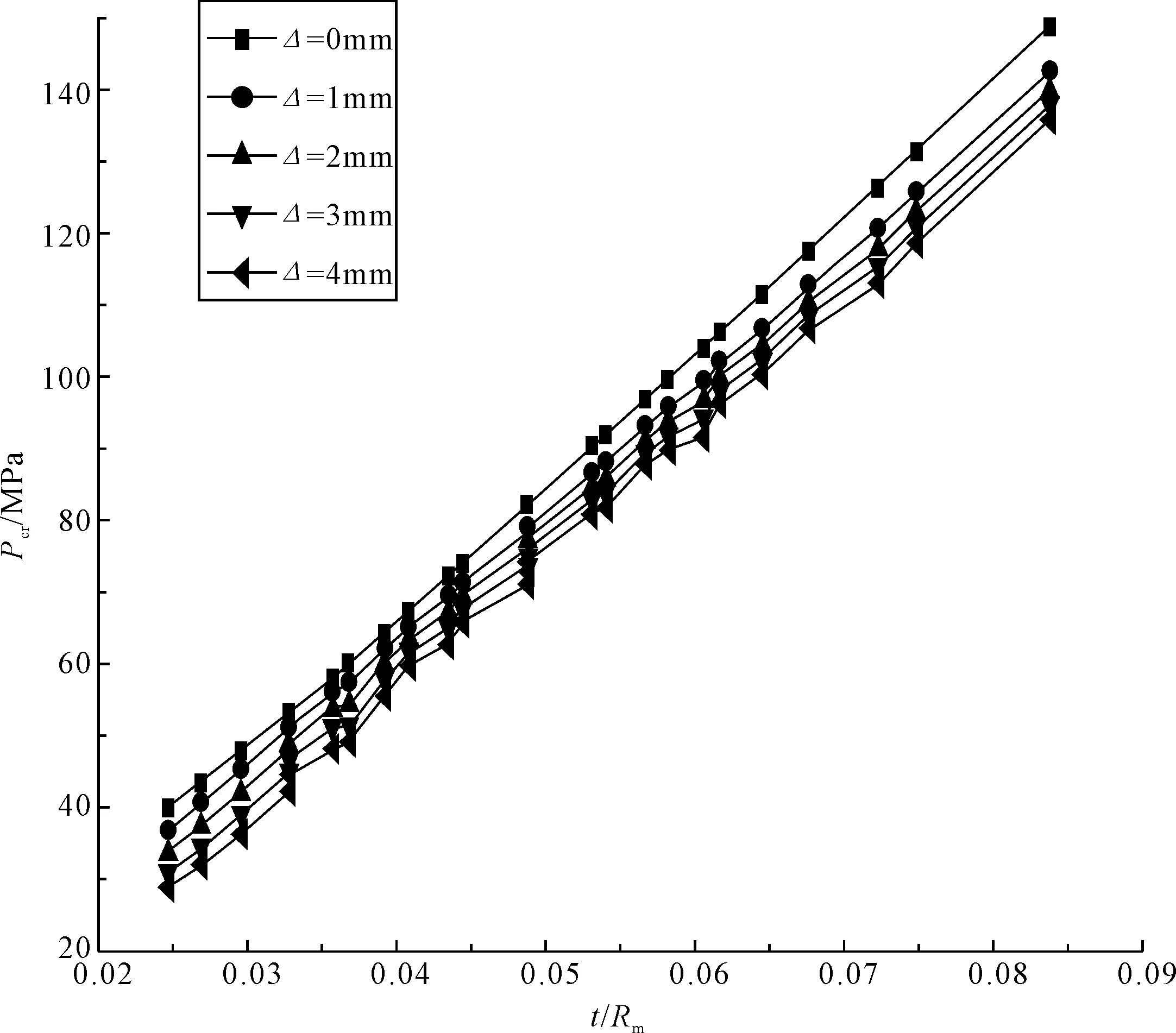
圖5 不同初始缺陷下厚度半徑比與極限強度間關系

式中:X1——球殼極限強度計算不確定系數;

X2——載荷不確定系數。

將式(6)代入到式(7)中，得到關于開孔球殼初始缺陷和開孔參數影響的極限狀態方程。

G(R,t,σy,θ,X1,X2,Δ,P)=

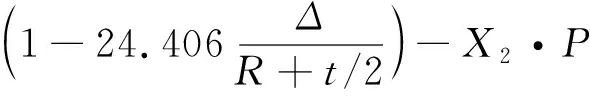
(8)

利用式(8)的極限狀態方程可以進行后續的結構可靠性分析。

3 極限強度可靠性計算與討論

3.1 隨機變量統計特性

參考圖6中ALVIN號的下潛數據進行載荷分析，利用Gumbel分布函數進行擬合，擬合結果見圖7所示，概率分布函數可以表示為

(9)

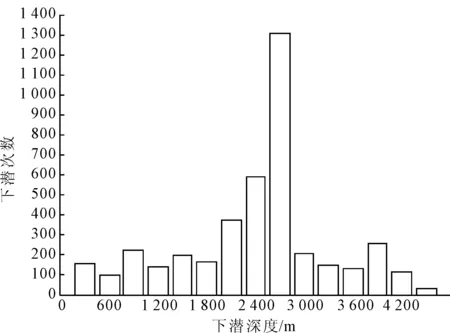
圖6 ALVIN號下潛載荷譜

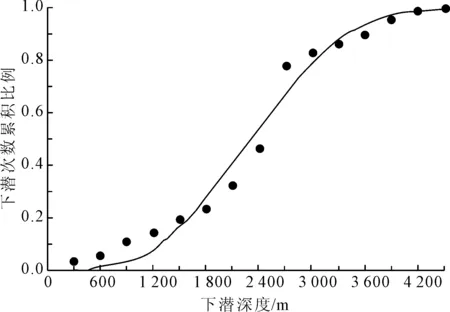
圖7 Gumbel分布擬合結果圖

再利用JC法[7]將非正態分布變量當量正態化，得到近似的正態分布函數的均值和變異系數。正態化后下潛深度的均值為2 408 m，變異系數為0.31。計算過程中考慮的參數還有球殼厚度t，球殼內半徑R等，其統計特征值見表2[8]。

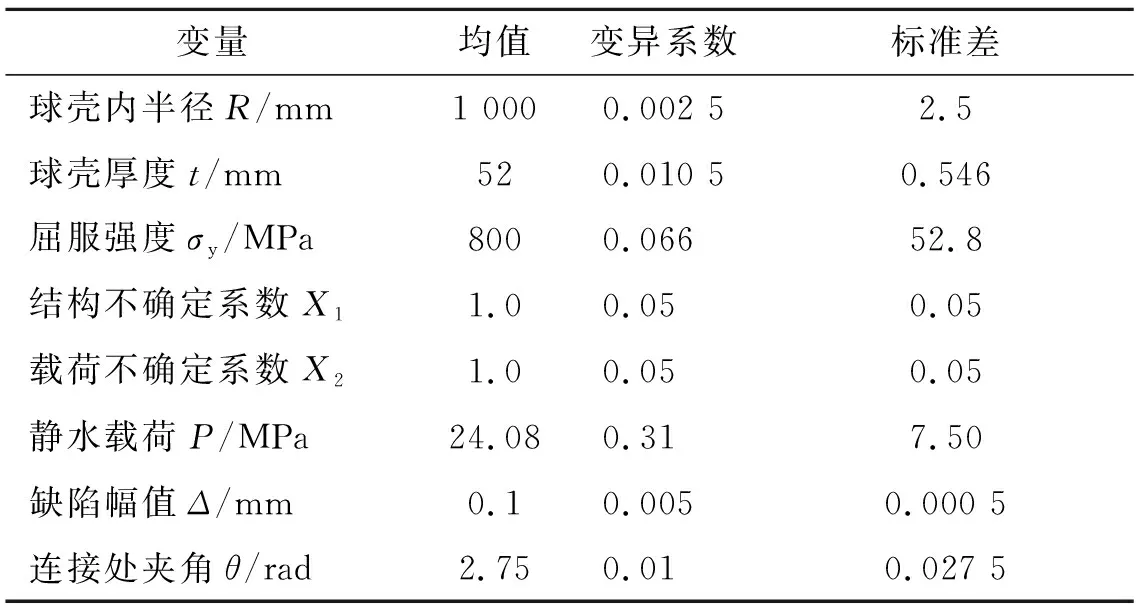
表2 鈦合金耐壓球殼基本變量的統計特性(均服從正態分布)

3.2 可靠性計算結果

采用改進一階二次矩法對式(8)球殼極限強度可靠性指標β進行計算，迭代結果見表3。

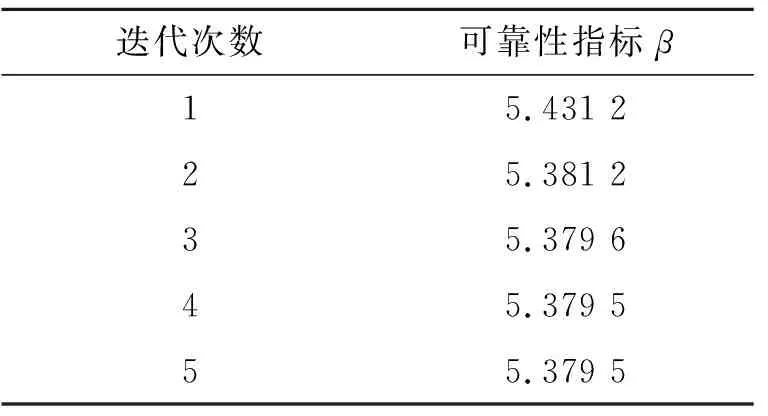
表3 含初始缺陷4 500 m鈦合金耐壓殼可靠性指標計算結果

由迭代結果可以看出，在迭代第5次時可靠性指標最后收斂在5.379 5。參考《工程結構可靠性設計統一標準》[9]和《建筑架構可靠度設計統一標準》[10]設定目標可靠性指標應不小于4.2。因此可以認為初始缺陷影響下4 500 m載人深潛器鈦合金開孔球殼結構極限強度可靠性是滿足要求的，結構失效的概率較低。

3.3 隨機變量對可靠性指標的影響

在潛水器耐壓球殼極限強度可靠性強度計算中包含了許多隨機變量，這些隨機變量的概率分布以及變異系數對可靠性指標的計算會產生一定的影響，且影響程度不一。

針對式(8)結構極限狀態方程分析各隨機變量變異系數對可靠性指標的影響。各隨機變量的影響程度，或極限強度可靠性對隨機變量靈敏度，可以通過變量的變異系數變化0.001時可靠性指標的變動幅值來評價。不同參數變異系數改變0.001時的可靠性指標變化幅值計算結果見表4。

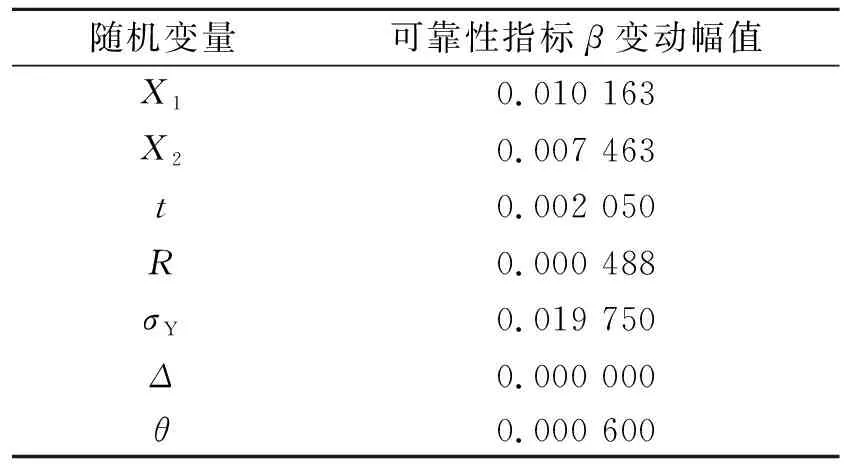
表4 變異系數改變0.001時可靠性指標變動幅值

各隨機變量的影響程度由大到小排列為材料屈服強度σ，連接處夾角θ，結構極限強度計算不確定系數X1，載荷不確定系數X2，球殼厚度t，球殼內半徑R，初始缺陷幅值Δ。各參數中影響最大的是材料的屈服強度，所以在考慮材料隨機特性的情況下要盡量保證材料均勻一致，其屈服強度在一個穩定的范圍內，進而提高球殼整體的安全性。連接處夾角θ對結構可靠性指標的影響較為明顯，應該在設計的過程中考慮弧度角過渡。

4 結論

1)提出球殼極限強度擬合公式的原型，通過大批量的有限元分析得到考慮開孔和初始缺陷的極限強度擬合公式，對于不同的開孔球殼可以由該擬合公式為基礎得到極限強度計算值。

2)基于極限強度擬合公式得到4 500 m載人深潛器鈦合金球殼極限狀態方程，可靠性指標計算表明，開孔和初始缺陷共同影響下鈦合金球殼極限強度可靠性指標為5.38，滿足目標可靠性要求，結構失效概率小。

3)通過可靠性指標計算分析了材料屈服強度、開孔連接處夾角、極限強度計算不確定系數、載荷不確定系數、球殼厚度、球殼內半徑、初始缺陷幅值等參數的對球殼極限強度可靠性的影響程度，并對鈦合金球殼的設計提出了建議。

[1] 施德培,李長春.潛水器結構強度[M].上海:上海交通大學出版社,1991.

[2] 陸 蓓,劉 濤,崔維成.深海載人潛水器耐壓球殼極限強度研究[J].船舶力學,2004,8(1):51-58.

[3] 王仁華,俞銘華.初始缺陷對深海載人潛水器耐壓球殼塑性穩定性影響[J].海洋工程,2005,23(4):111-115.

[4] PAN Binbin.An overview of buckling and ultimate strength of spherical pressure hull under external pressure[J].Marine Structures,2010,23:227-240.

[5] PAN B B,CUI W C,SHEN Y S.Experimental verification of the new ultimate strength equation of spherical pressure hulls[J].Marine Structures,2012,29:169-176.

[6] 陳承皓,薛鴻祥,唐文勇.基于全壽命擴展模型的鈦合金球殼疲勞可靠性分析[J].上海交通大學學報,2013,47(2):307-311.

[7] 趙國藩.工程結構可靠度[M].北京:科學出版社,2011.

[8] 謝祚水,王自力.潛艇結構分析[M].武漢:華中科技大學出版社,2004.

[9] GB50153-2008.工程結構可靠性統一設計標準[S].北京:中華人民共和國建設部,2008.

[10] GB50068-2001.建筑結構可靠性統一設計標準[S].北京:中華人民共和國建設部,2001.

[11] 江曉俐.船舶結構極限強度可靠性分析方法研究[J].船海工程,2005(4):1-3.