水潤滑艉軸承水膜厚度與壓力數(shù)值計(jì)算分析

，，

(1.海軍駐大連426廠軍事代表室 大連 116000；2.中國艦船研究設(shè)計(jì)中心 武漢 430064)

水潤滑艉軸承結(jié)構(gòu)簡單，不產(chǎn)生滑油污染，在船舶上使用越來越多[1]。但由于水潤滑軸承內(nèi)襯材料多為高分子材料，變形比較大，如不考慮彈性變形會對軸承水膜壓力與厚度的計(jì)算精度產(chǎn)生影響。文獻(xiàn)[3-4]討論了橡膠高彈性材料的彈性變形、初值選取對水潤滑軸承彈流潤滑計(jì)算的影響，但未涉及飛龍、賽龍等其它軸承高分子材料，也未考慮船舶艉軸傾斜的影響，在工程實(shí)際應(yīng)用中有一定的局限性。飛龍、賽龍是艦船水潤滑艉軸承常用的高分子材料，自潤滑性能好，彈性模量比橡膠大，但卻比金屬材料低得多。其變形量及最小膜厚比值與橡膠材料一樣，不是一個高階無窮小量。若忽略這個變形量，水膜厚度與壓力以及承載能力的計(jì)算將產(chǎn)生較大誤差，尤其在艉軸傾斜時更為嚴(yán)重。因此，計(jì)算時應(yīng)考慮軸承內(nèi)襯彈性變形和艉軸傾斜，這有助于提高承載能力的計(jì)算精度，以滿足軸承負(fù)荷設(shè)計(jì)要求。

1 艉軸承結(jié)構(gòu)及裝配

船舶水潤滑艉軸承由外襯、內(nèi)襯組成。外襯為銅套，內(nèi)襯多為飛龍等非金屬材料，見圖1。艉軸承與螺旋槳軸的裝配見圖2。

軸承內(nèi)襯與軸襯套的相關(guān)幾何參數(shù)和材料物理性能參數(shù)見表1、表2所列。

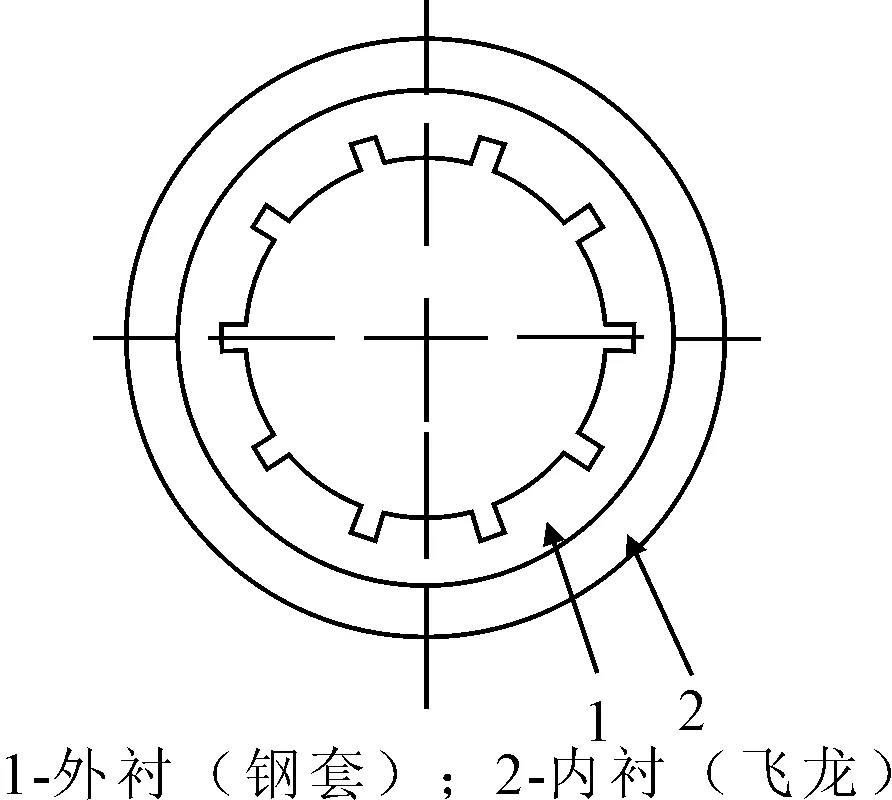
圖1 軸承結(jié)構(gòu)示意

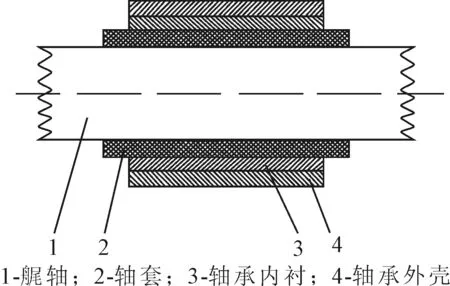
圖2 船舶艉軸承裝配示意

表1 軸承的幾何參數(shù)

軸承內(nèi)徑/mm內(nèi)襯厚度/mm軸承長度/mm水槽夾角/(°)水槽個數(shù)/個水粘度(20℃)/(Pa·s)軸承間隙/mm350453504100.0011

表2 軸承內(nèi)襯與軸襯套材料物理性能

2 彈流潤滑求解流程

2.1 不計(jì)彈性變形的水膜壓力與厚度計(jì)算

假定軸承在流體動壓潤滑狀況下，求解軸承水膜厚度與壓力可應(yīng)用雷諾方程[5]

(1)

式中：h——水膜厚度；

η——水的粘度；

U——滑動速度；

p——壓強(qiáng)。

令φ=x/r，λ=z/(l/2)，

H=h/c=1+εcos (φ-θ)

(2)

式中：ε——偏心率;

θ——偏位角;

c——軸承半徑間隙。

P = p/p0，p0= 2ωμ/ψ2，ψ = c/r為相對間隙，即可得到量綱-的量形式

(3)

求解時，將艉軸承展開成一平面模型,見圖3。

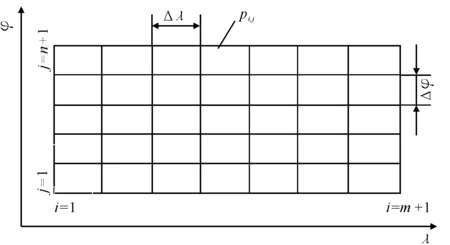
圖3 網(wǎng)格劃分示意

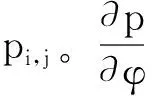
Ai,jpi+1,j+Bi,jpi-1,j+Ci,jpi,j+1+Di,jpi,j-1-Ei,jpi,j=Fi,j

(4)

式中:各系數(shù)為

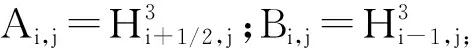
Ei,j=Ai,j+Bi,j+Ci,j+Di,j；

Fi,j=3Δφ(Hi+1/2,j+Hi-1/2,j)。

上式可產(chǎn)生(m-1)×(n-1)個方程，在給定的膜厚h下可求解pi,j。在水膜壓力pi,j作用下，軸承內(nèi)襯所產(chǎn)生的變形通過有限元法來求解。

2.2 有限元法求解軸承彈性變形

作用于軸承的水膜壓力屬于分布力p(s)。在彈性力學(xué)中，若有分布力作用于半無限平面上，那么在寬度為ds的微元上將產(chǎn)生p(s)ds的集中力,見圖4。分布力p(s)在M處所產(chǎn)生的彈性變形方程為[6-7]

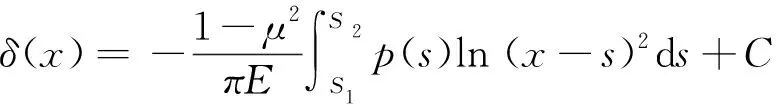
(5)

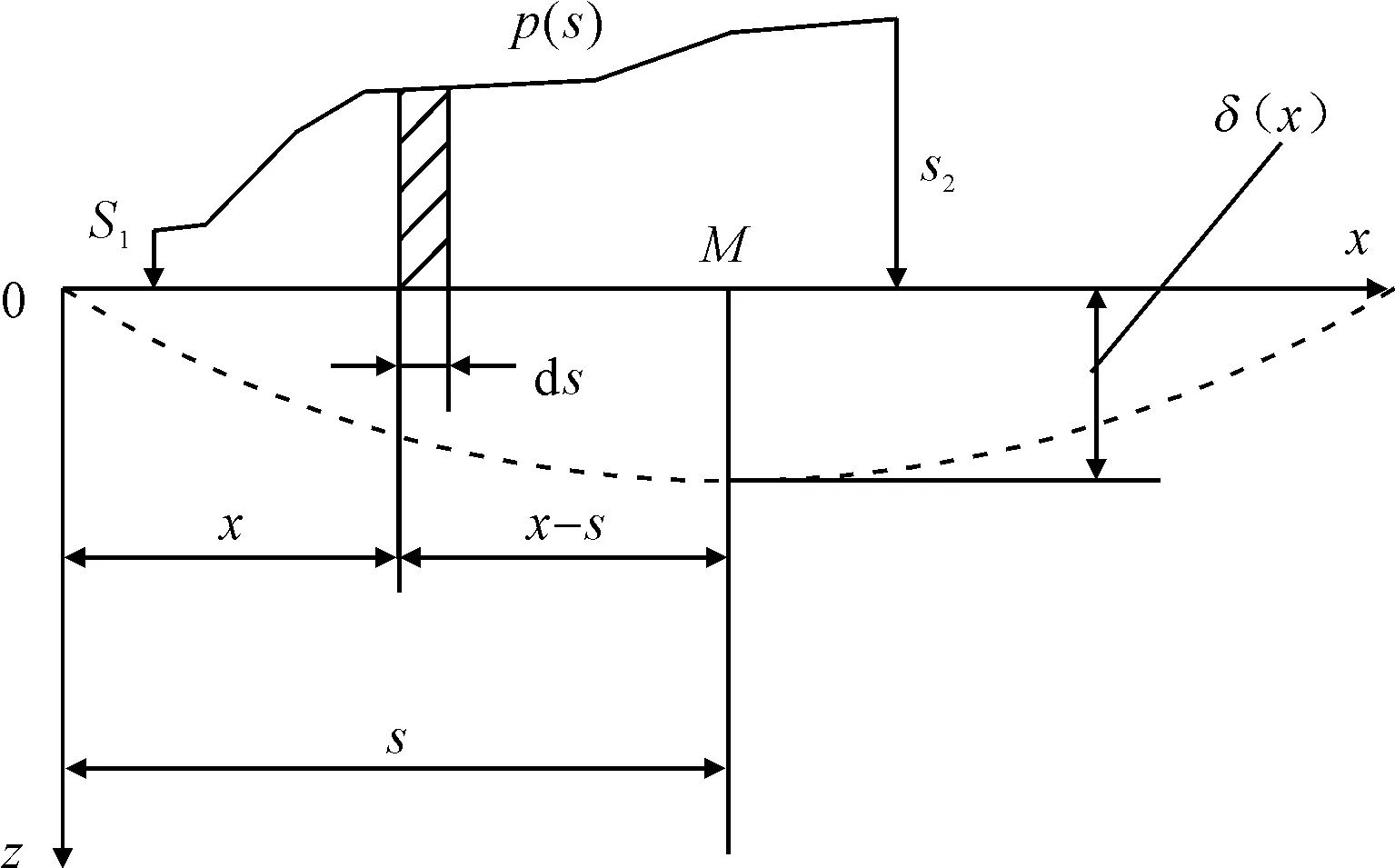
圖4 分布力作用下的變形

應(yīng)用有限元方法求解軸承內(nèi)襯彈性變形時，將連續(xù)體離散成有限個微小單元，如正六面體微小單元由8個節(jié)點(diǎn)組成，每個節(jié)點(diǎn)有3個位移自由度，共有24個，見圖5。

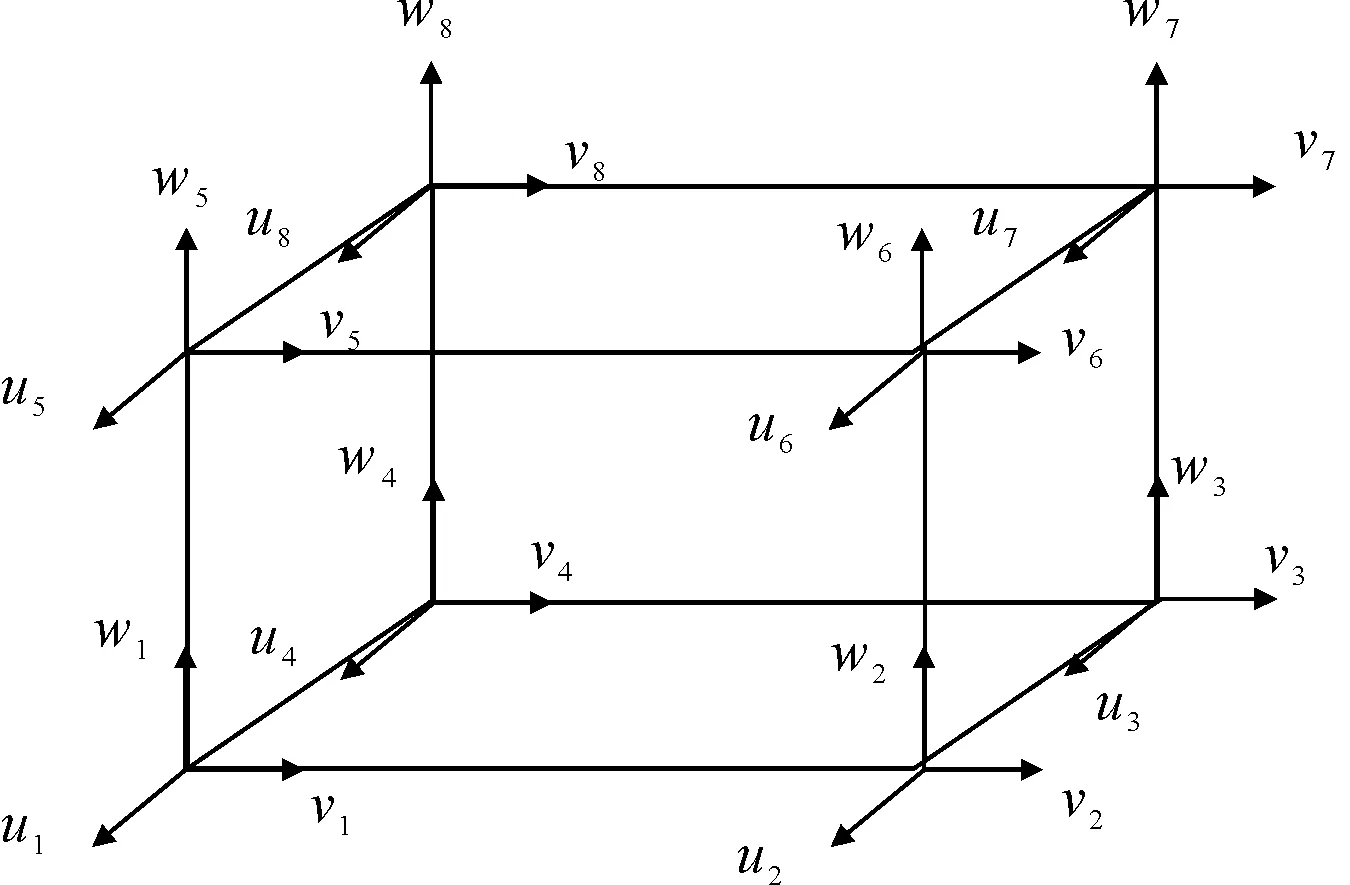
圖5 8節(jié)點(diǎn)正六面體單元

該單元的節(jié)點(diǎn)位移列陣qe和節(jié)點(diǎn)力列陣Fe分別為

(6)

(7)

式中:ui、vi、wi——x、y、z方向位移;

Fi——節(jié)點(diǎn)作用力。

將該單元的勢能對其節(jié)點(diǎn)位移qe求一階極值，那么可得到單元的剛度狀態(tài)方程：

(8)

式中:Ke——單元節(jié)點(diǎn)剛度矩陣。

節(jié)點(diǎn)力列陣Fe中的上表面節(jié)點(diǎn)z向上的力與前一次計(jì)算得到的水膜壓力矩陣一一對應(yīng)，節(jié)點(diǎn)力列陣中的其他元素置為零。同樣，求出節(jié)點(diǎn)位移陣qe后，提取其中的上表面節(jié)點(diǎn)z向上的位移對應(yīng)加入到水膜厚度矩陣中。

2.3 彈流潤滑求解流程

水潤滑艉軸承彈流動壓潤滑求解流程見圖6。

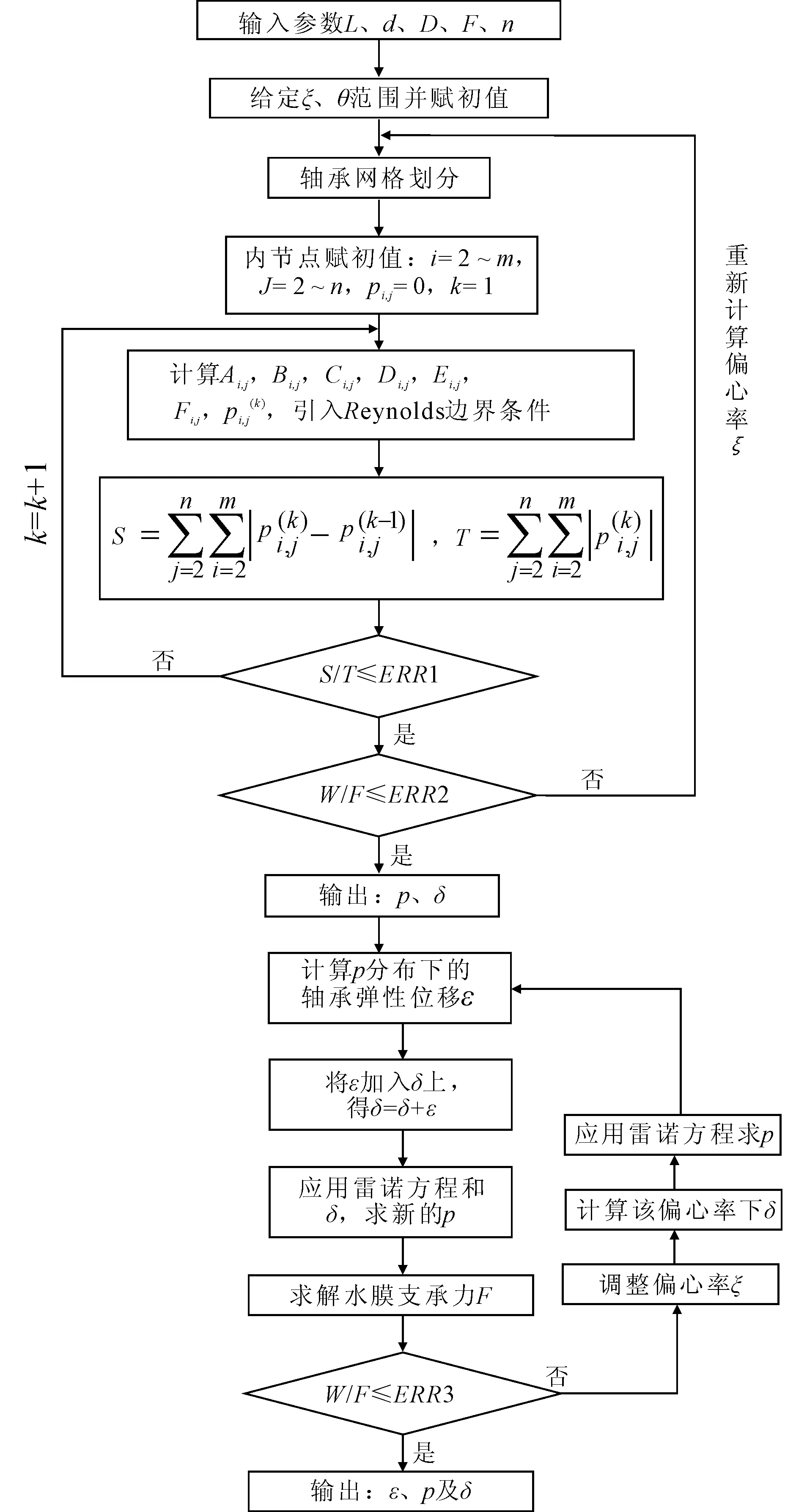
S-前后兩次迭代過程中的水膜壓力合力誤差(pi+1-pi);T-迭代后的水膜壓力合力；W-水膜壓力積分計(jì)算后得到的垂向合力;F-外部垂向載荷。圖6 軸承彈性變形量計(jì)算技術(shù)路線

首先給定軸承長度L、內(nèi)徑d、載荷F、軸頸外徑D、轉(zhuǎn)速n、彈性模量E、泊松比ν，以及軸承的偏心率ξ和偏位角θ的大致范圍并設(shè)定初始值。根據(jù)假定的軸承潤滑水膜厚度δ，求水膜壓力分布p。如果水膜承載力W與軸承外載荷F的差值在規(guī)定的誤差范圍內(nèi)，則初次計(jì)算結(jié)束，否則重新調(diào)整偏心率ξ和偏位角θ繼續(xù)計(jì)算。當(dāng)計(jì)算完畢后，用有限元法求解該水膜壓力p下軸承內(nèi)襯各個節(jié)點(diǎn)處的垂向彈性變形量ε，并將其加入到初次計(jì)算得到的水膜厚度δ上，得到新的潤滑水膜厚度分布，重新計(jì)算水膜壓力p和厚度δ，并比較此時的水膜承載力W與軸承負(fù)荷F間的差值。若差值超過規(guī)定，則重新調(diào)整軸承的偏心率。每次偏心率調(diào)整后須重新依次確定：水膜厚度→水膜壓力→彈性變形→水膜厚度→水膜壓力，這5個步驟為一個循環(huán)。經(jīng)過多次循環(huán)，直至計(jì)入彈性變形后得到的水膜承載力W與軸承外載荷F相當(dāng)，完成彈流動壓潤滑求解。

3 計(jì)算結(jié)果與分析

水潤滑艉軸承彈性流體動壓潤滑與流體動壓潤滑計(jì)算時，設(shè)定軸承的正上方為0°，軸旋轉(zhuǎn)方向?yàn)轫槙r針，軸承與軸頸的接觸表面絕對光滑。

為解決艉軸承水槽導(dǎo)致水膜不連續(xù)這一問題，假定軸承兩水槽間的板條壓力分布狀況為中間高兩側(cè)低，兩水槽內(nèi)的流體壓力為0，則可應(yīng)用雷諾方程求解單個板條的水膜厚度和壓力。

下面就艉軸的傾斜狀況，在相同工況下進(jìn)行艉軸承彈性流體潤滑(彈性)與流體動壓潤滑(剛性)的兩種計(jì)算方法對比。

3.1 不考慮艉軸傾斜

水潤滑軸承水膜厚度與壓力的兩種計(jì)算方法差別在于水膜厚度和壓力計(jì)算是否計(jì)入軸承內(nèi)襯的彈性變形。

當(dāng)不考慮艉軸傾斜時，在不同線速度、比壓下，艉軸承最大水膜壓力pmax與最小水膜厚度hmin的兩種計(jì)算結(jié)果見圖7～10。

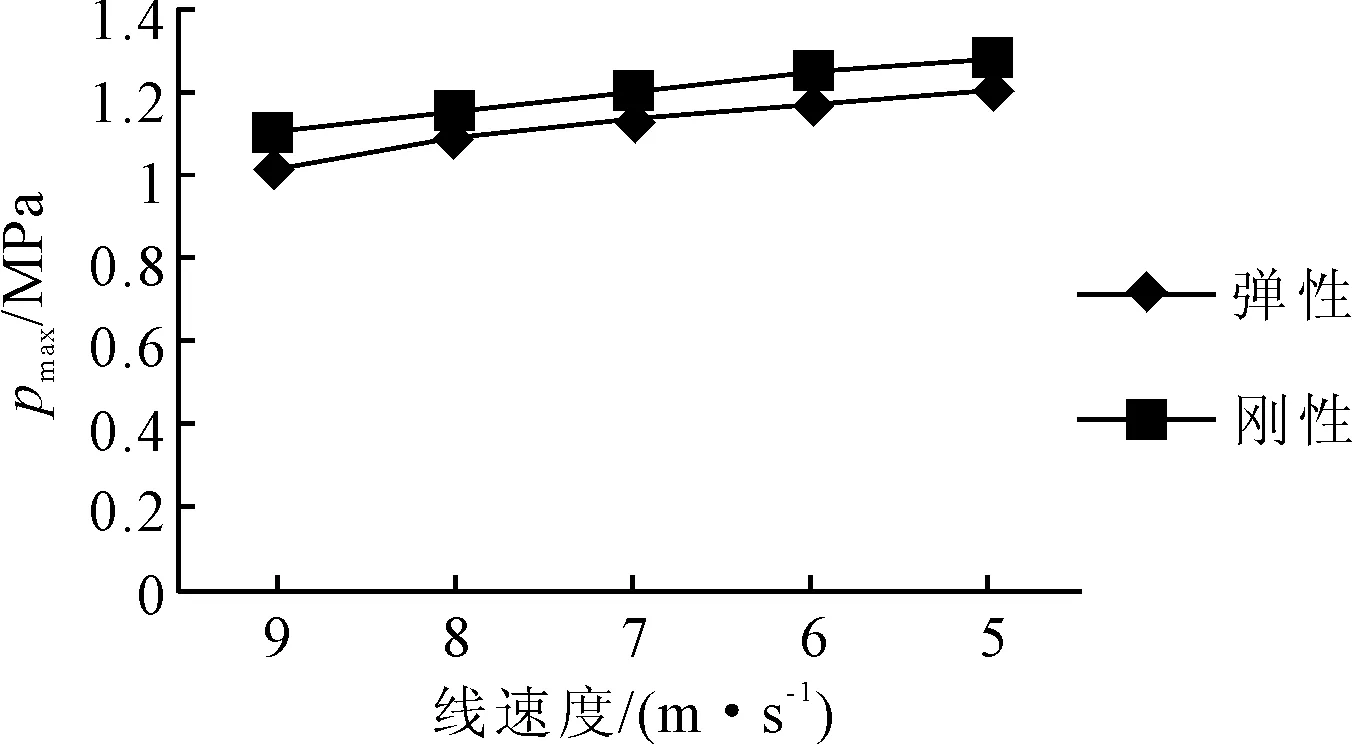
圖7 p=0.1 MPa時pmax的兩種計(jì)算結(jié)果

圖8 p=0.1 MPa時hmin的兩種計(jì)算結(jié)果

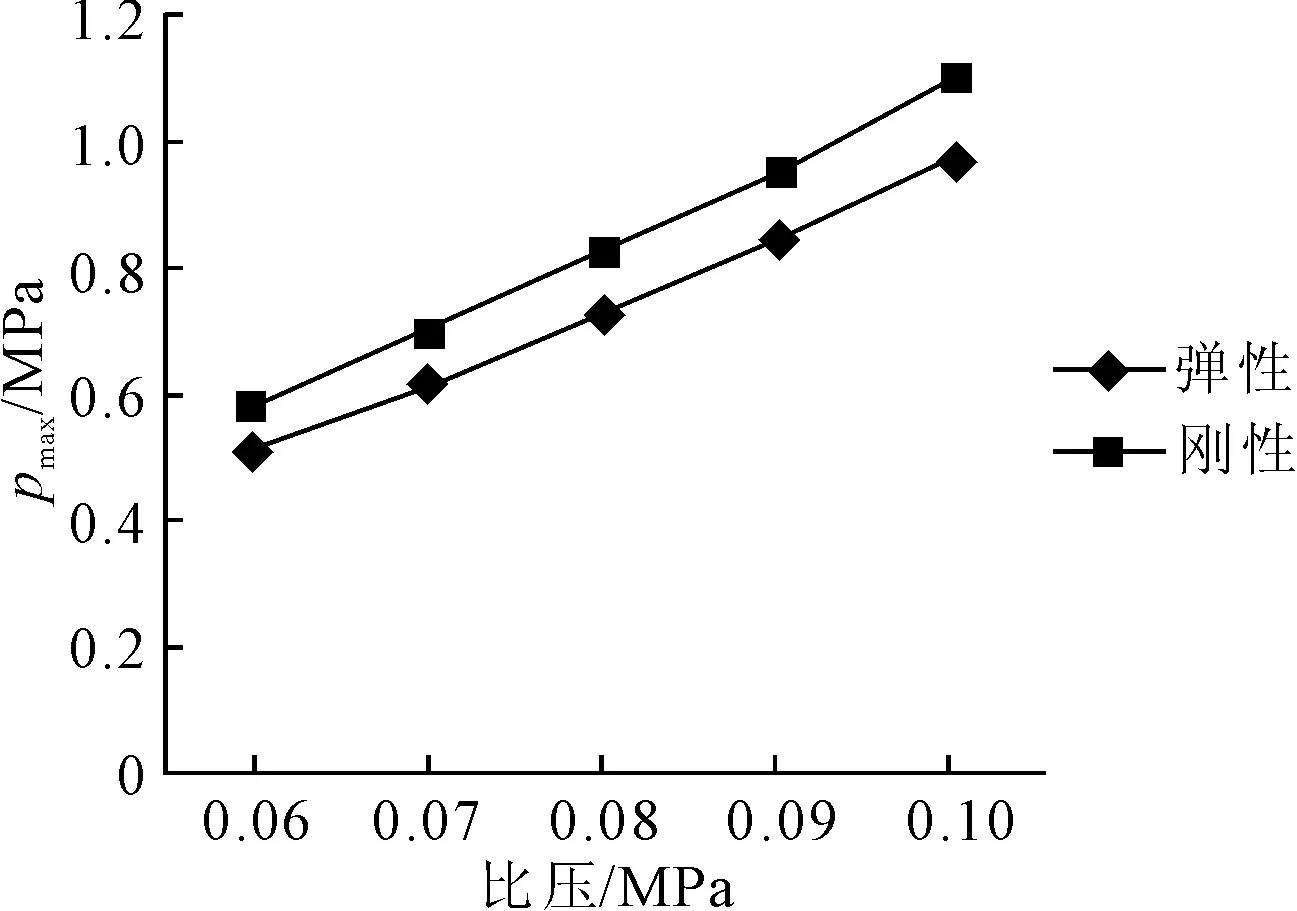
圖9 v=9 m/s時pmax的兩種計(jì)算結(jié)果

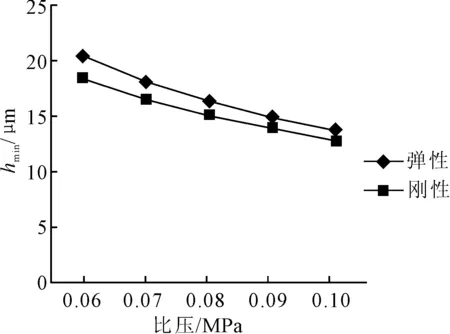
圖10 v=9 m/s時hmin的兩種計(jì)算結(jié)果

從圖7～10可見，在相同的線速度和比壓下，艉軸承的彈流動壓潤滑與流體動壓潤滑計(jì)算結(jié)果相比，前者的最大水膜壓力相對較小，最小水膜厚度相對較大。這說明計(jì)入內(nèi)襯材料彈性變形時，在工作比壓不變情況下，可降低最大水膜壓力，增加水膜厚度，使得壓力分布趨于平緩。

3.2 考慮艉軸傾斜

假定艉軸傾斜率為艉軸相對于艉軸承兩端面的垂向偏移距離的差值與軸承半徑間隙的比值，計(jì)算p=0.10 MPa，v=9 m/s時軸承的水膜壓力與厚度。

不同傾斜率下的兩種計(jì)算結(jié)果見圖11、12。

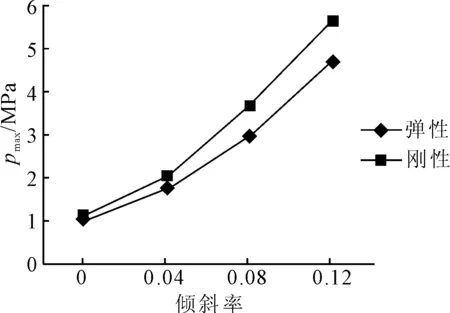
圖11 不同傾斜率下pmax的兩種計(jì)算結(jié)果

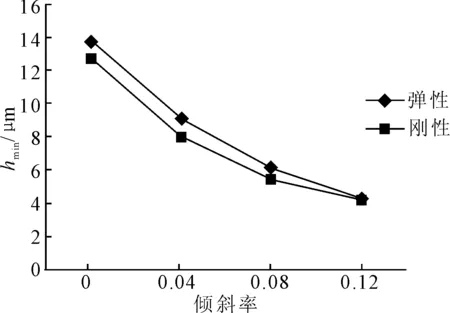
圖12 不同傾斜率下hmin的兩種計(jì)算結(jié)果

由圖11、12可見，隨著艉軸傾斜率的增加，兩種計(jì)算方法的最大水膜壓力均逐漸增大，最小水膜厚度同樣逐漸減小。與流體動壓潤滑相比，艉軸承的彈流動壓潤滑的最大水膜壓力較小，最小水膜厚度較大。

以彈性流體動壓為例。艉軸計(jì)算結(jié)果表明，在相同工況下(p=0.10 MPa，v=9 m/s)，考慮艉軸傾斜(傾斜率為0.12)時，彈流水膜壓力為4.8 MPa，是艉軸不傾斜時的4.8倍。艉軸不傾斜時彈流水膜厚度14 μm，是艉軸傾斜(傾斜率為0.12)時的4.1倍。由此可見，在工程計(jì)算中，考慮艉軸傾斜效應(yīng)有助于提高計(jì)算精度。

4 結(jié)論

1)在工程計(jì)算中，考慮艉軸承的彈性變形與艉軸傾斜率有助于提高水膜壓力與厚度的計(jì)算精度。

2)與不考慮彈性變形相比，在相同工況下計(jì)入艉軸承內(nèi)襯的彈性變形后，最大水膜壓力pmax減小，最小水膜厚度hmin增加。

3)隨著艉軸傾斜率的增大，彈流潤滑最大水膜壓力pmax上升，最小水膜厚度hmin減小。

在軸承彈性流體動壓潤滑計(jì)算中，本文沒有考慮熱流效應(yīng)對水粘壓效應(yīng)以及水膜壓力與厚度的影響，今后可在這一方面繼續(xù)開展研究，進(jìn)一步完善計(jì)算方法。

[1] 楊和庭，唐育民.船舶水潤滑艉管橡膠軸承的設(shè)計(jì)[J].武漢造船，2000(2)：19-22.

[2] 王 寧.基于MATLAB的滑動軸承壓力分布數(shù)值計(jì)算[D].大連:大連理工大學(xué)，2006

[3] 吳文蕾.多重網(wǎng)格法計(jì)算有限長線接觸熱彈流問題初值對求解過程的影響[J].摩擦學(xué)學(xué)報(bào),2008(3)：177-181.

[4] 段芳莉，韋云龍.彈性變形對徑向軸承彈流潤滑性能的影響[J].潤滑與密封,2000(6)：9-11.

[5] 劉 宇，劉正林，吳鑄新，等.基于MATLAB的軸向開槽水潤滑徑向軸承性能分析[J].潤滑與密封，2009，34(4)：71-73.

[6] Hirani Harish, Verma Manish.Tribological study of elas-tomeric bearings for marine propeller shaft system[J].Tribology International，2009，42：378-390.

[7] 溫詩鑄，楊沛然.彈性流體動力潤滑[M].北京：清華大學(xué)出版社，1992.