Mathematica軟件在大學物理問題數值模擬中的應用舉例*

韓永勝 楊宏新 馬 軍*中國藥科大學教改課題(2013)

(中國藥科大學理學院 江蘇 南京 210029)

1 引言

隨著科學技術的進步，特別是計算機技術的發展，數值模擬已經成為繼科學實驗和理論分析之后人們認識世界的新手段．在大學物理教學中，引入數值模擬對培養學生的創造力和想象力具有事半功倍的作用．本文就Mathematica軟件在大學物理問題數值模擬中的應用做點介紹．Mathematica軟件是美國Wolfram Research公司開發的一款科學計算軟件，于1988推出了第1版，2012年底推出了第9版．新版將很多的新功能集成到系統的內核中，使其成為一款非常卓越的集符號運算、數值運算和計算結果可視化于一體的科學計算軟件．公司的總裁和軟件的主要開發者斯蒂芬·沃爾夫雷姆(Stephen Wolfram)先生是學物理出身，在軟件設計中更多考慮了在物理學方面應用的方便性，使得這款軟件特別適合物理學工作者和學生使用[1]．下面我們通過幾個具體的例子來說明Mathematica在大學物理問題數值模擬方面的應用．

2 Mathematica在力學問題數值模擬中的應用

考慮一個繞過質心的軸旋轉飛行中的足球，除了受到重力mg和空氣阻力fg的作用外，還受到馬格努斯力fM的作用，因此，它在空間將劃出一個弧線，這就是大家所熟知的“香蕉球”[2]．可以用Mathematica編程模擬一個“香蕉球”的運動軌跡．

設足球場平面為xOy平面，足球繞過質心的豎直軸以角速度ω旋轉，足球質心運動的速度v=vxi+vyj+vzk，空氣密度為ρ，足球半徑為R．假定空氣阻力與速度平方成正比，空氣的摩擦力矩是恒定值，這樣角加速度是常量β．利用牛頓第二定律可以列出如下的矢量方程

(1)

上式中G=mg，fg和fM可以表示為

k1(-vxi-vyj-vzk)v

(2)

(3)

根據實際情況，相應參數選擇如下：阻力系數c=0.5，空氣密度ρ=1.29 kg/m3，足球半徑R=

0.11 m，足球的質量m=0.44 kg，則可計算得k1=0.012 3，k2=0.014 4．在數值模擬中，將角加速度β取1rad/s2，初始條件定為：r(0)=0，v(0)=24i+16j+8.5k(m/s)，ω0=15krad/s，足球距離球門25 m處．

數值求解的思路如下：

利用列表表示足球的角速度矢量

ω=0,0,ω0-βt

位置矢量

r=xt,yt,zt

速度矢量用位置矢量的導數表示

v=Dr,t

利用Norm函數求矢量的模，利用Cross函數計算矢量的叉乘，可將式(2)和式(3)寫成

G=0,0,-mg

fg=-k1Normvx't，y't,z't

fM=k2Crossω,v

由式(1)寫出足球運動的動力學矢量方程

eqns=mDr,t,2=

fM+fg+G//Thread

將常數和初始條件用規則表示，利用NDSolve函數數值求解足球運動的微分方程組，得到解x(t)、y(t)、z(t)．利用畫線函數Line畫出球門，利用三維參數作圖函數ParametricPlot3D畫出足球在三維空間的運動軌跡，并利用Show函數將球門和球的軌跡畫在一張圖上，如圖1所示．

圖1 足球飛行軌跡

將飛行時間定義為Manipulate函數的動態變量，用畫點函數Point和畫線函數Line動態畫出足球位置和飛行軌跡，形成足球在空間飛行過程的動畫，如圖2所示．

(a)

(b)

通過修改參數和初始條件可以模擬出不同情況下足球的運動情況，可對練習“香蕉球”提供一定的理論上的指導．

3 Mathematica在李薩如圖形數值模擬中的應用

李薩如圖形是振動合成中的一個典型例子[3]．當質點同時參與兩個振動頻率成整數比的相互垂直的運動時，質點的運動軌跡是閉合的，其軌跡在x方向的切點數nx和y方向的切點數ny的比值，與x方向振動頻率νx和y方向振動頻率νy的比值的倒數相等，即

x=Axcos(2πνxt+φx0)

(4)

y=Aycos(2πνyt+φy0)

(5)

當νx∶νy=n∶m，其中n，m為自然數，則

(6)

Mathematica程序設計思路如下：將式(4)和式(5)中的振幅、頻率、初相以及時間作為Manipulate函數的動態變量，利用二維參數作圖函數ParametricPlot畫出合振動曲線，利用畫點函數Point畫出振動質點的位置，并用Show函數將其畫在一張圖上，從而演示李薩如圖形并動態顯示質點的運動，如圖3所示．

(a)

(b)

可以通過調節水平方向和數值方向振幅和頻率的比值，以及水平方向和豎直方向的初相位來得到不同情況下的李薩如圖形，還可以演示質點的運動軌跡，可用來研究李薩如圖形的性質．

4 Mathematica在點電荷電場數值模擬中的應用

應用Mathematica軟件模擬兩個點電荷電場線和電勢的分布．由于兩個點電荷激發的電場和電勢分布是關于兩電荷連線旋轉對稱的，故畫出過兩電荷連線的平面(設為xOy平面)的電場和電勢分布即可．設電荷量為q1和q2的兩個點電荷，相距為2r0，以兩電荷連線為x軸，兩個點電荷連線的中點為坐標原點建立xOy坐標系，則坐標平面內的電勢分布為

電場分布為

E=-U

(8)

程序設計思路如下：

根據式(7)，將U定義為電荷量以及坐標的函數，并將電荷量q1和q2定義為Manipulate函數的動態變量，利用ContourPlot函數畫出等勢線分布，利用StreamPlot函數畫出負的電勢梯度函數(即電場函數)對應的電場分布．為使電場線疏密能合理地表示電場大小，可以點電荷為圓心，貼近電荷處的圓周上均勻設定電場線經過的點，如圖4所示．

(a)

(b)

圖4顯示了兩種點電荷分布(q1=3,q2=-3;q1=1,q2=1)下的電場和電勢分布情況．可動態改變左右電荷的電荷量，從而得到不同點電荷電荷量情況下的電場和電勢分布．

5 Mathematica在牛頓環數值模擬中的應用

牛頓環可以看作是一塊平凸透鏡和一塊平板玻璃構成的空氣膜的上下表面反射光的干涉，當上面的平凸透鏡上下移動時，牛頓環圖像會呈現出視覺上的“干涉條紋陷入”和“干涉條紋冒出”的現象，這可以通過Mathematica編程來模擬[4]．

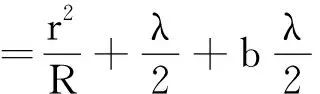
(9)

對應的相位差為

(10)

干涉光的強度分布為

(11)

令牛頓環條紋所在的平面為xOy平面，則r2=x2+y2．設平凸透鏡的曲率半徑為R=1 m，入射光的波長為λ=589.3 nm，牛頓環的顯示范圍為{(x,y)|

-x0≤x≤x0,-y0≤y≤y0}，并取x0=y0=

0.003 m，程序編制思路如下：將式(10)中的b定義為Manipulate函數的動態變量，利用密度圖函數DensityPlot畫出式(11)的強度分布，如圖5所示．

(a)

(b)

6 小結

結合以上幾個實例發現，利用Mathematica軟件，可以通過編程將實際的物理過程通過數值模擬的方式表現出來．Mathematica程序通俗易懂，編程工作量小，編程用的語言接近自然語言，表示方法也接近通常的數學習慣表示，因而能讓使用者集中精力考慮物理問題的數學模型，不用在編程上花上太多精力．將Mathematica軟件引入大學物理教學中，對培養學生的創新能力和提高物理思維能力都是非常有益的．

參考文獻

1 唐曙光.在物理教學中使用Mathematica.物理通報,2003(10):25～26

2 馬濤.數字化大學物理.杭州：浙江大學出版，2008

3 黃海林,李元杰.李薩如圖形的計算機模擬——大學物理CAI軟件開發實例.物理與工程,2003,13(3)：38～41

4 鐘季康,鮑鴻吉.大學物理習題計算機解法——MATLAB編程應用.北京：機械工業出版社，2008