懸架液壓襯套液固耦合有限元分析
秦 民,蔣永峰,馬天飛,劉亞川,張敏敏
(1.中國第一汽車股份有限公司技術中心,長春 130012; 2.吉林大學汽車仿真與控制國家重點實驗室,長春 130022)
懸架液壓襯套液固耦合有限元分析
秦 民1,蔣永峰1,馬天飛2,劉亞川2,張敏敏2
(1.中國第一汽車股份有限公司技術中心,長春 130012; 2.吉林大學汽車仿真與控制國家重點實驗室,長春 130022)
液壓襯套作為汽車懸架系統的重要隔振元件,其靜、動特性分析和隔振性能匹配在其研究開發中具有重要意義。利用液固耦合有限元方法對液壓襯套進行建模分析,通過靜態和動態仿真與試驗的對比驗證了模型的正確性。仿真計算襯套關鍵參數,為后期的試驗和參數化分析提供指導,并利用該方法對參數化分析結果進行了結構驗證。
液壓襯套;液固耦合;有限元分析
液壓襯套作為懸架控制臂與車身之間的連接件和隔振件,通過在橡膠襯套基礎上封裝液體,使其能在較廣的頻率范圍內提供大阻尼[1],因此在中高級乘用車懸架系統中得到廣泛應用。研究液壓襯套動態特性對改善懸架振動性能具有重要意義。
作為液壓隔振元件,液壓襯套和液壓懸置有諸多相似之處,因此在對液壓襯套的研究中大多借鑒液壓懸置的研究方法。上官文斌[2]建立了橡膠懸置的液固耦合有限元模型,通過仿真計算對靜、動特性、液室與慣性通道的壓力分布、慣性通道中液體流速分布等進行了研究,提出在對懸置低頻動特性進行仿真時,應用液固耦合有限元方法可得到比集總參數模型更好的結果。史文庫等[3-4]運用有限元與試驗相結合的方法對某輕型卡車駕駛室液壓懸置進行了性能匹配,研究了懸置各參數對其動特性的影響規律。潘孝勇[5]建立了基于網格疊加橡膠隔振器黏彈塑性材料模型,并將其應用于液壓襯套液固耦合分析中。Gil-Negrete[6]對利用ABAQUS建立的橡膠主簧結構模型和FLUENT建立的液體模型進行聯合仿真分析,預測了液壓襯套的動態特性。Karlsson等[7]利用試驗獲取模型參數,根據橡膠襯套的頻率相關性及振幅相關性的特性建立液壓襯套的橡膠部分模型。
本文利用計算流體力學和有限元相結合的方法對某汽車懸架液壓襯套進行建模和仿真分析,通過試驗驗證了模型正確性,并利用該模型計算液壓襯套關鍵物理參數,最后利用有限元模型對液壓襯套AMESim參數化模型優化方案進行了仿真驗證。
1 液壓襯套結構和原理
本文研究的徑向式液壓襯套結構如圖1(a)所示,安裝在某乘用車下控制臂和副車架相連的部位,用于減少振動的傳遞,改善乘坐舒適性。液壓襯套三維幾何模型如圖1(b)所示。
液壓襯套的金屬內套與橡膠主簧內表面硫化為一體,用于連接副車架;尼龍限位塊與金屬內套固結,防止載荷過大破壞襯套;橡膠主簧是承載和減振的重要部分;對稱布置的2個液室通過斜的慣性通道相連;金屬外套與金屬骨架過盈配合(之間添加橡膠密封環),將油液(乙二醇水溶液)密封在液室中,并連接懸架下控制臂。

圖1 液壓襯套結構
當液壓襯套的金屬內、外套在液室方向發生徑向相對位移時,一個液室受壓縮變小,而另一液室受拉伸變大,油液通過慣性通道在兩液室中不斷地來回流動。液體通過慣性通道時出現能量損失(沿程損失、摩擦損失等),從而產生較大阻尼,實現快速減振。當通道中的液柱產生共振時,能量損失消耗最快,相應的阻尼滯后角也會達到最大值[2]。這時其阻尼滯后角可達到傳統橡膠襯套的8~10倍[5]。在更高的頻率其阻尼滯后角將下降。
2 建立液壓襯套的液固耦合有限元模型
2.1 液壓襯套固體有限元建模
1)固體網格的劃分。將液壓襯套三維幾何模型導入前處理軟件HyperMesh中進行適當的幾何清理,如將不關注的倒角刪除等。金屬外套固定在下控制臂孔中,剛度很大,在有限元模型中可以省略。然后對襯套固體部分的各個零件分別進行體單元劃分,得到液壓襯套固體有限元網格模型,如圖2所示。模型共有23 362個體單元,其中22 406個8節點六面體單元,956個6節點五面體單元。金屬內套與限位塊之間的粘結、各金屬件與橡膠主簧之間的硫化都用節點擬合來模擬[8]。
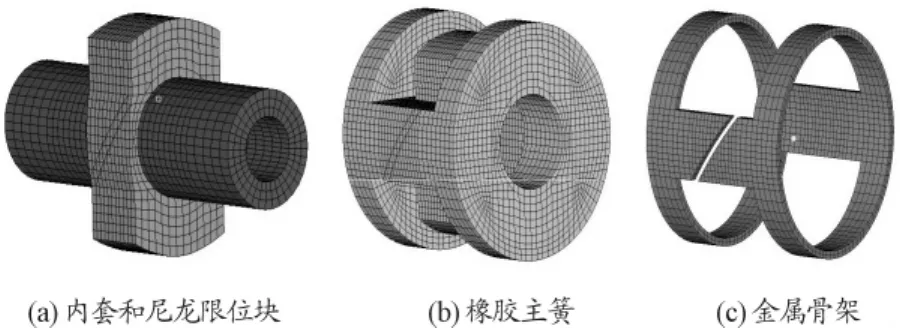
圖2 液壓襯套固體有限元網格模型
2)各零件材料屬性的確定。考慮到橡膠主簧的非線性特性(滯后角一般在3°~5°)遠小于液壓襯套整體非線性特性,為了縮短模型計算時間,對其進行線性化處理。各零件材料屬性如表1所示。
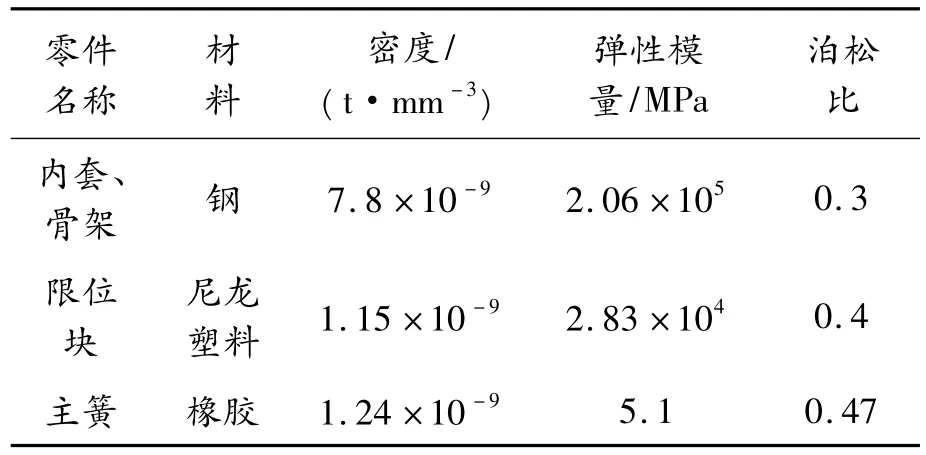
表1 材料參數表
3)固體有限元模型建立。將液壓襯套固體網格導入ADINA-Structure中,然后對襯套的各零件分別賦予材料屬性。
液壓襯套的主芯(包含金屬骨架、限位塊和橡膠主簧)與金屬外套是通過金屬骨架傳力的,所以在金屬骨架對應的節點施加6個自由度的全約束。
與臺架試驗加載方式相一致,有限元模型載荷施加在金屬內套內表面的節點。在進行靜、動特性仿真時,施加載荷的類型和方式是不同的,需要通過不同的時間步和時間函數來實現。
通過上述設置,建立了液壓襯套固體有限元模型,如圖3所示。

圖3 液壓襯套固體有限元模型
2.2 液壓襯套液體有限元建模
1)液體網格的劃分。對液壓襯套的液體幾何模型進行網格劃分時,需保證固體結構和液體結構相接觸的界面上的節點和單元一致。得到的液體網格如圖4所示。該網格模型有9 260個單元,其中68個6節點的FCBI單元,9192個8節點的FCBI單元。

圖4 液壓襯套液體有限元網格模型
2)液體材料屬性的確定。液壓襯套中的油液為乙二醇水溶液,經試驗測得其體積百分數為90%,密度為1.121×10-9t/mm3,20℃時的動力黏度為1.295×10-8MPa·s。
3)液體有限元模型的建立。將HyperMesh中的液體有限元網格導入到ADINA-F中進行材料和邊界條件的設定。考慮到液壓襯套主要是在低頻下工作,慣性通道中的液體流速較低,按雷諾數的計算公式,可估算出襯套內液體的最大雷諾數小于臨界雷諾數2 300,因此可將模型中的液體流動定義為層流(laminar)[9]。
液壓襯套的液體邊界主要有2種:由于金屬外套剛度大且固定不動,同時考慮液體有一定的黏性,將液體與外套接觸的界面定義為無滑移固壁;橡膠主簧剛度比金屬材料小得多,液體與橡膠接觸界面會在載荷作用下進行運動,因此將此界面定義為無滑移液固耦合面。在定義液固耦合面時,要注意和固體中的液固耦合面一一對應。
液壓襯套液體有限元模型如圖5所示。
3 液固耦合有限元仿真與試驗驗證
3.1 靜態仿真與試驗驗證
靜態仿真一般采用Statics方法,但為了研究液體對靜特性的影響,本文采用準靜態方法,即緩慢加載(加載時間盡量長),使動態仿真逼近靜態仿真。在動態緩慢加載過程中,液室和慣性通道中的液體流動比較緩慢,可以按層流處理。本文只研究液體起作用方向上的隔振性能,因此把該方向作為加載方向(X向),其他兩個方向不做研究。加載載荷從0 N均勻增長到1 000 N,時間歷程為25 s。

圖5 液壓襯套液體有限元模型
通過上述設置,將固體有限元模型和液體有限元模型分別導入液固耦合求解模塊ADINA-FSI中進行耦合仿真,仿真結果在后處理模塊ADINAProcessing中輸出,如圖6所示。從圖6可知,橡膠主簧的變形主要發生在與內套接近的部位。
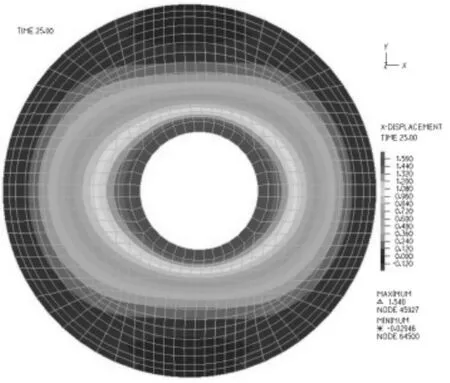
圖6 橡膠主簧X向變形圖(mm)
圖7為加載過程中t=25 s時刻的液體壓力分布圖,可見在準靜態加載過程中,由于是均勻緩慢加載,故襯套內液體壓力分布比較均勻且壓力值很小。
為了驗證有限元仿真的正確性,對液壓襯套進行臺架試驗。在靜剛度測量中,試驗機從0 N開始以40 N/s的速度對襯套X向進行勻速力加載,加載時間為25 s。
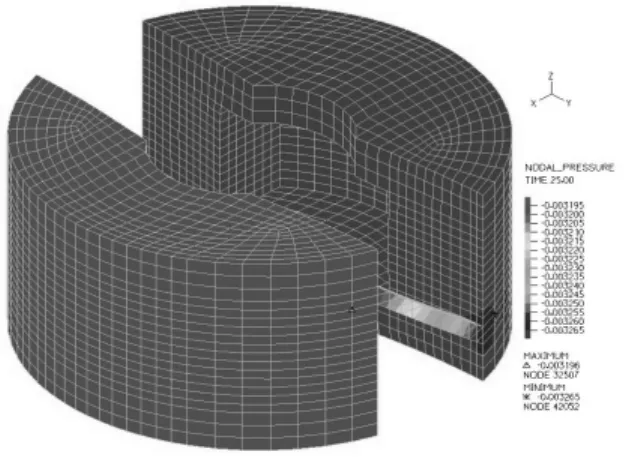
圖7 液體壓力分布圖(MPa)
根據仿真和試驗數據繪制力-位移曲線,如圖8所示。可見,有限元模型對襯套靜剛度的模擬是正確的。在大變形狀態下襯套的靜剛度出現非線性,而有限元模型由于對橡膠材料進行了簡化而不能進行模擬。

圖8 液壓襯套仿真靜剛度與試驗值
3.2 動態仿真與試驗驗證
對襯套內套上的所有節點施加X向的位移諧波激勵,激勵幅值為0.375 mm,頻率選取了1~40 Hz內幾個典型值。利用幾何作圖法[10]計算這些頻率下的動剛度和阻尼滯后角,得到該振幅下的動剛度曲線和阻尼滯后角曲線,如圖9所示。
液壓襯套動剛度和阻尼滯后角仿真曲線與試驗曲線的趨勢相吻合,但數值偏小,且隨著頻率增大偏差變大。數值偏小是由于有限元模型對實際結構進行了簡化,同時忽略了橡膠主簧本身的阻尼造成的。將橡膠材料作為線彈性材料處理不能模擬出橡膠主簧動剛度隨著頻率增大而變大的趨勢。
綜上分析,建立的液壓襯套液固耦合有限元模型是正確的,但在實際應用過程中需要進行適當的修正。

圖9 動態特性試驗和仿真曲線
4 有限元方法計算液壓襯套體積剛度
體積剛度用來反映液室壁面膨脹能力。設液室內壓力變化為ΔP時,由壓力變化導致液體體積變化ΔV,則體積剛度定義如下:

獲得體積剛度一般有2種方法:試驗法[11]和有限元分析法[2]。試驗法更精確,但方法復雜不易操作。有限元分析法容易實現且成本低。固定液壓襯套的內、外套,增加液室中液體的體積,測量液室內的壓力,獲得體積與壓力的變化關系,即可計算得到體積剛度。
由于液壓襯套的兩個液室是相同的,且慣性通道對液室的體積剛度沒有影響,所以將慣性通道去掉并取一半模型進行有限元分析,如圖10所示。其中液體模型中增加了一個小立方體網格單元,用于增加液室中液體的體積。
將上面的網格單元導入ADINA進行設置。固體模型中對金屬內套和金屬骨架外表面施加固定約束,液體模型中與金屬外套接觸的液體表面和小立方體4個側表面均定義為固壁,小立方體頂面定義為移動壁面。對移動壁面施加X向位移載荷,將小立方體中的液體推入液室。仿真時間為10 s。圖11為第6 s時刻的仿真結果。
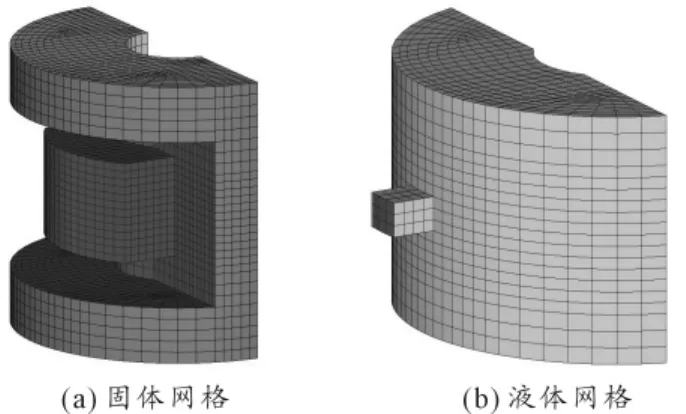
圖10 用于計算體積剛度的有限元模型
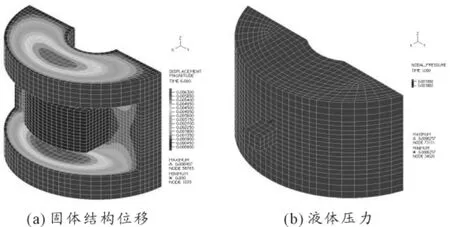
圖11 模型仿真結果
固體模型結果反映出液室體積膨脹主要發生在上下兩端橡膠壁面上,壁面厚度和橡膠材料參數直接影響體積剛度。液體模型反映出液體壓力的變化。由于模型是緩慢加載,所以壓力分布基本是均勻的,只需測得一點的壓力值即可代表整體壓力。
根據仿真過程中液室中油液體積和壓力的變化,可以得到單液室體積剛度為 2.62×1011Pa/m3。
5 利用有限元模型驗證參數化模型優化結果
液壓襯套的AMESim參數化建模能夠方便快捷地計算襯套各參數對其動特性的影響,進而通過改變不同參數實現襯套性能的優化[8],但優化結果是否在結構上滿足需要,需要通過有限元法驗證。
本文所研究的液壓襯套通過AMESim參數化建模與分析得到阻尼滯后角曲線,見圖12(a)。圖中常見振幅曲線對應的峰值頻率區間為7~15 Hz。為了匹配整車懸架系統,需將頻率區間移到11~17 Hz。利用參數化模型進行優化(優化結果見圖12(b)),所得最優方案需對慣性通道的長度和截面積進行修改。
根據優化結果修改有限元模型,其仿真結果如圖13所示,與AMESim仿真結果一致。
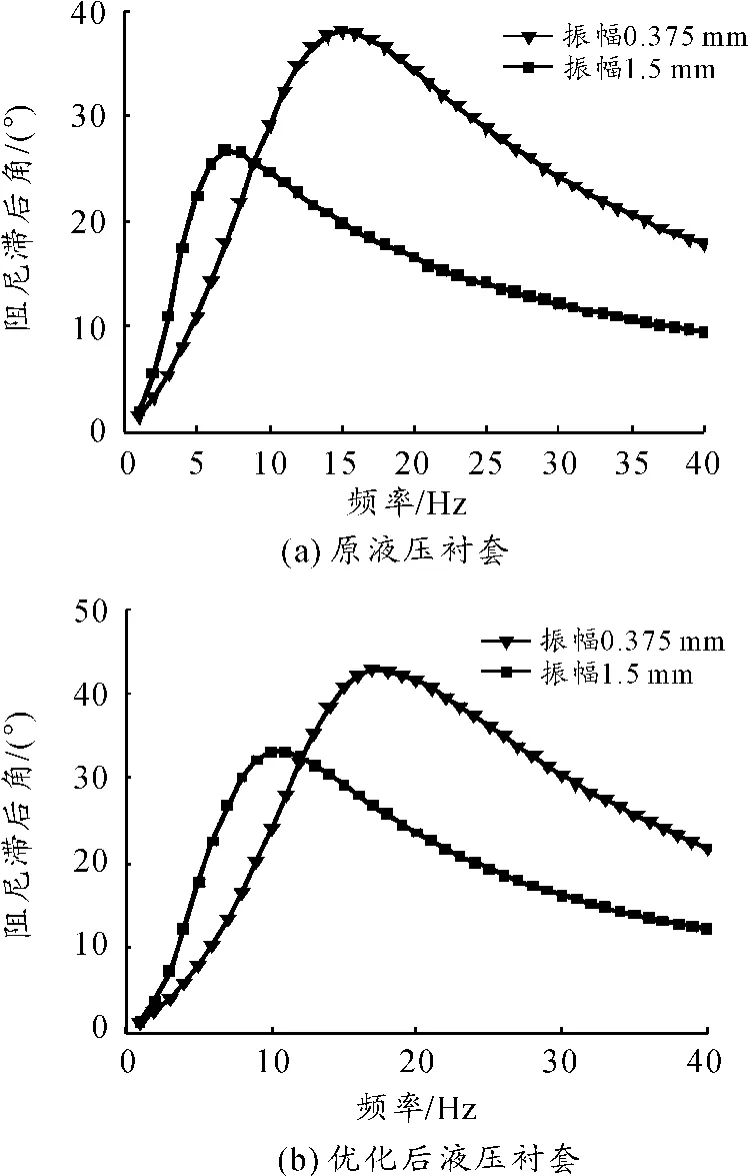
圖12 優化前后液壓襯套的阻尼滯后角

圖13 有限元仿真結果
6 結論
利用ABAQUS和ADINA建立了液壓襯套的液-固耦合有限元模型,仿真分析其靜、動態特性并進行試驗驗證。在此基礎上仿真計算其關鍵參數體積剛度,得到如下結論:
1)該有限元模型能夠有效模擬液壓襯套的靜、動態特性,為進一步對襯套進行動力學性能改進提供基礎。
2)利用有限元方法可以獲得液壓襯套液室體積剛度,為相關參數化分析工作提供指導和借鑒。
3)有限元方法可以對襯套參數化模型優化結果進行結構驗證。
[1] 上官文斌,徐馳.汽車懸架控制臂液壓襯套動態特性實測與計算分析[J].振動與沖擊,2007,26(9):7-10.
[2] 上官文斌.液阻型橡膠隔振器液-固藕合動力學特性仿真技術研究[D].北京:清華大學,2003.
[3] SHI Wen-ku,CHEN Zhi-yong.Finite Element Analysis of the Static and Dynamic Characteristics of Engine Rubber Mount[Z].PACIIA,2009.
[4] CHEN Zhi-yong,SHI Wen-ku.Finite Element Analysis of Light Vehicle Cab’s Hydraulic Mount Based on Fluid-Structure Interaction Method[J].SAE,2011(1):604.
[5] 潘孝勇.橡膠隔振器動態特性計算與建模方法的研究[D].浙江:浙江工業大學,2009.
[6] Gil-Negrete N.Predicting thedynamicbehaviourof hydrobushings[J].Shock and Vibration,2002,12:91-107.
[7] Karlsson F,Persson A.Modelling non-linear dynamics of rubber bushing-Parameter Identification and Validation[D].Sweden:Master’s Dissertation,Lund University,2003.
[8] 劉亞川.懸架液壓襯套有限元分析與基于AMESim的隔振性能優化[D].長春:吉林大學,2013.
[9] 岳戈,梁宇白.ADINA流體與流固耦合功能的高級應用[M].北京:人民交通出版社,2010.
[10]王光(譯).硫化橡膠動態性能試驗方法[J].噪聲與振動控制,1987,3:52-57.
[11]呂振華,上官文斌.液阻懸置動態特性實驗方法及實測分析[J].中國機械工程,2004,15(2):182-186.
(責任編輯 劉 舸)
Fluid-structure Interaction Finite Element Analysis of Hydrobushing Used in Suspension
QIN Min1,JIANG Yong-feng1,MA Tian-fei2,LIU Ya-chuan2,ZHANG Min-min2
(1.R&D Center,China Faw Co.Ltd.,Changchun 130012,China; 2.State Key Laboratory of Automobile Simulation and Control,Jilin University,Changchun 130022,China)
As the important vibration isolator used in suspension system,analyses of static and dynamic characteristics and matching of vibration isolate performance for hydrobushing are important in research and development.Based on fluid-structure interaction finite element method,FSI finite element model of hydrobushing is built.The static and dynamic simulation of the FSI model are conducted to validate the model.Based on the verified model,key parameters of hydrobushing are simulated.The parameters will provide guidance for the test and parametric analysis.Meantime,the method is used to verify the results of parametric analysis.
hydrobushing;fluid-structure interaction;finite element analysis
U463
A
1674-8425(2014)07-0005-06
10.3969/j.issn.1674-8425(z).2014.07.002
2014-05-08
吉林省科技支撐計劃資助項目(20106003)
秦民(1974—),男,吉林長春人,博士研究生,高級工程師,主要從事車輛操穩平順性研究。
秦民,蔣永峰,馬天飛,等.懸架液壓襯套液固耦合有限元分析[J].重慶理工大學學報:自然科學版,2014 (7):5-10.
format:QIN Min,JIANG Yong-feng,MA Tian-fei,et al.Fluid-structure Interaction Finite Element Analysis of Hydrobushing Used in Suspension[J].Journal of Chongqing University of Technology:Natural Science,2014(7):5-10.

