Prelec概率權重函數先驗行為假設拓展
王金山,李偉兵
(陸軍軍官學院 a.基礎部;b.研管大隊2隊,合肥 230031)
Prelec概率權重函數先驗行為假設拓展
王金山a,李偉兵b
(陸軍軍官學院 a.基礎部;b.研管大隊2隊,合肥 230031)
提出一種稱為中值不變性的概率權重函數先驗行為假設,提供一種推導Prelec概率權重函數的新方法,并給出更弱條件下滿足中值不變性的定義。分析并闡述了中值不變性較已知的3種先驗假設在可行性和可靠性兩個方面的綜合優勢,其結論更容易被人們接受,對決策者有實際參考意義。至此,存在4種可推導出Prelec概率權重函數的先驗行為假設。
前景理論;Prelec權重函數;先驗行為假設拓展;中值不變性
期望效用理論被用于解決風險決策問題之后,因其嚴謹的公理體系和簡潔的數學形式,很快成為風險決策理論的重要基石,然而在決策過程中并非偶然出現的一系列悖論對其提出了挑戰。對此,Kahneman和Tversky[1]提出了著名的前景理論,試圖對決策選擇一系列問題中的異常現象做出合乎數理的解釋。他們將人的決策過程分為編輯和評價兩個階段,提出了用權重函數和價值函數共同度量總體價值,具體來說是結果價值與決策權重的乘積。價值類似于效用理論中的效用值,決策權重是概率的函數,通過它描述概率在決策者決策心理過程中發揮的作用并度量其影響。因此,前景理論決策過程中Von Neumann-Morgenstern的公理體系不再適用。為了完善前景理論,Kahneman和Tversky[2]又提出了累積前景理論。累積前景理論通過累積概率替代個別概率的方法轉換效用函數中的客觀概率。他們思索決策者的風險態度有4種不同的類型:當結果出現的概率較大時,處于收益狀態下決策者風險厭惡,損失狀態則風險偏好;但當概率較小時,決策者的風險態度正好相反。Prelec在累積前景理論基礎上發展了概率權重函數,并首次基于復合不變性假設推導出了一類概率權重函數,即Prelec概率權重函數,此后它被廣泛用于前景理論決策中。
風險選擇的先驗行為假設對基本的決策模型有很大的影響,因此對先驗行為假設的拓展研究是前景決策理論研究的熱點。本文在復合不變性的基礎上,提出一種稱為中值不變性的先驗行為假設,并提供一種推導Prelec概率權重函數的新方法。中值不變性更容易被人們接受,很好地拓展了先驗行為假設。
1 基本假設
決策者在決策時會面對一系列結果和概率,用X表示所有結果構成實數結果集,P表示所有結果對應發生概率構成的概率集。假設決策者的偏好是通過價值函數u:X→R給定的,價值的大小決定決策者的偏好程度,對于任意x,y∈X,當且僅當u(y)>u(x)時,y優于 x;當且僅當 u(y)= u(x)時,y與x無差異。若用(x,p)表示以概率為p得到結果x的事件;用((y,q),p)表示以概率p得到(y,q)的事件;用(x,p;y,q)表示以概率p得到結果x并且以概率q得到結果y的事件,滿足p +q≤1。假設決策者的概率權重函數是通過w:p→[0,1]給定的,函數w(p)在(0,1)上連續、單調遞增,且滿足w(0)=0,w(1)=1。
假設總體價值是通過總體價值函數U:(X,P)→R給定,是結果集X和概率集P的函數。當且僅當U(X,P)=U(Y,Q)時,(X,P)與(Y,Q)無差異,記作(X,P)~(Y,Q)。對于給定結果的價值函數u(x)以及概率權重函數w(p),U(X,P)滿足以下運算規則:
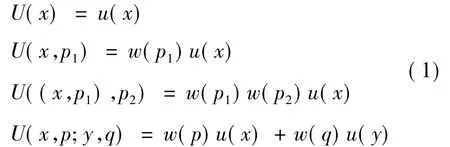
假設價值函數u(x)和概率權重函數w(p)在式(1)的運算規則下,構成前景理論中總體價值的表示方法。
2 現行概率權重函數先驗行為假設
在前景理論研究領域,風險選擇的先驗行為假設對基本的決策模型有很大的影響,主要表現在概率權重函數的設置上。Prelec[3]首先基于復合不變性(compound invariance)假設導出了Prelec概率權重函數;Luce[4]提出了一種相對于復合不變性假設而言更為簡單的還原不變性(reduction invariance);Al-Nowaihi和Dhami[5]在還原不變性基礎上又提出了冪不變性(power invariance)。
2.1 復合不變性
定義1[3]若對于任意結果x,y∈X和概率p,q,r,s∈[0,1],(x,p)~(y,q)和(x,r)~(y,s)同時成立,且對于任意結果x',y'∈X,?λ≥1,λ∈N+,若(x',pλ)~(y',qλ)成立,則(x',rλ)~(y',sλ)亦成立,則稱概率權重函數w滿足復合不變性。
Prelec的研究結果[3]顯示復合不變性假設下的概率權重函數如式(2)所示,稱式(2)的函數w為Prelec概率權重函數。
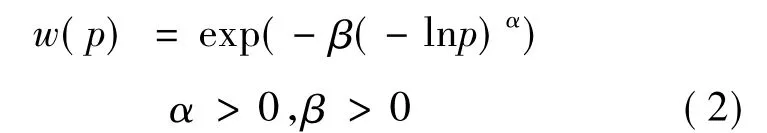
定理1[3]概率權重函數w滿足復合不變性,當且僅當其是Prelec權重函數。
2.2 還原不變性
定義 2[4]若對任意結果 x∈X和概率p,q,r∈[0,1],λ∈{2,3},若((x,p),q)~(x,r)成立,則((x,pλ),qλ)~(x,rλ)亦成立,則稱概率權重函數w滿足還原不變性。
定理2[4]概率權重函數w滿足還原不變性,當且僅當其是Prelec權重函數。
2.3 冪不變性
定義3[5]若對任意結果,p,q∈[0,1],λ∈{2,3},若((x,p),p)~(x,q)成立,則((x,pλ),pλ)~(x,qλ)亦成立;若(((x,p),p),p)~(x,q)成立時,則亦成立,則稱概率權重函數w滿足冪不變性。
定理3[5]概率權重函數w滿足冪不變性,當且僅當其是Prelec權重函數。
3 中值不變性的拓展
本部分基于Prelec的復合不變性提出了區別于3種現行的不變性假設的一種新的先驗行為假設,稱之為中值不變性(Mid-value invariance)。首先給出函數中值和函數中值不變性的定義。
定義4 類似于p,q和r滿足pr=q2,稱q是p和r的幾何中值;若p,q和r在函數 w下滿足w(p)·w(r)=w2(q),則稱p是r和q在w(·)下的函數中值。
定義5 若q是p和r在w(·)下的函數中值,對?λ≥1,λ∈N+,w(pλ)·w(rλ)=w2(qλ)亦成立,即qλ亦是pλ和rλ的函數中值,則稱函數w滿足函數中值不變性。
在定義1中,加入2個關于結果和概率的條件qλ和r=q后,可得到一種新的不變性假設,為便于定義1與定義4進行對比,記y'為z,記s為r,因函數w(p)滿足定義5的函數中值不變性,故稱此不變性為中值不變性。
定義6 若對任意結果x,y∈X和概率p,q,r∈[0,1],(x,p)~(y,q)和(x,q)~(y,r)同時成立,若對?λ≥1,λ∈N+,z∈X,(y,pλ)~(z,qλ)成立,則(y,qλ)~(z,rλ)亦成立,則稱概率權重函數w滿足中值不變性。
定理4 概率權重函數w滿足中值不變性,當且僅當其是Prelec權重函數。
證明:根據定義6的已知條件,若概率權重函數w滿足中值不變性,則有

對于式(12),當且僅當G(Q)=βQα,α,β>0才成立,式(12)整理后得
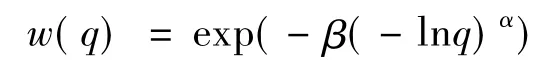
4 更弱條件的中值不變性
事實上,類似于還原不變形[4]和冪不變性[5]的更弱條件,在定義6中,概率權重函數滿足中值不變性所需的條件是可以減弱的。
定理5 當λ=2,3時概率權重函數滿足中值不變性,則對?λ>0,λ∈R+概率權重函數均滿足中值不變性。


命題(21)的正確使得λ'=λ-1=2-k·3-l,可極大地拓展取值空間,通式為
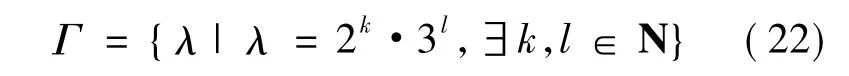
在前文推導過程中k,l∈N+,由于命題(21)的成立使得k,l∈N,而Γ在正實數域R+上是稠密的[7],因此可把Γ的取值拓展到正實數域R+內。證畢。
據此可得到較定義6條件更弱的定義7。
定義7 對任意結果x,y∈X和概率p,q,r∈[0,1],(x,p)~(y,q)和(x,q)~(y,r)無差異關系同時成立,且對λ∈{2,3},z∈X,成立,則亦成立,則稱概率權重函數w滿足中值不變性。
5 先驗行為假設比較分析
先驗行為假設的合理與否主要體現在可行性和可靠性2個方面。可行性包括結論的可行性;可靠性包括假設條件的可靠性和所得結論的可靠性。下文將就這2個方面進行分析,對比4種不同先驗行為假設,并闡述中值不變性在先驗行為假設可行性和可靠性的綜合優勢。
5.1 合理性分析
先驗行為假設條件所需的概率為客觀概率。事實上,有很多決策問題的客觀概率不清楚或者不能通過實際的準確計算得到,因此決策過程中的概率多是憑經驗或相關理論推斷得到的主觀概率,而主觀概率存在不穩定性,這一點已被Ellsberg悖論完整體現并證明。故在先驗行為假設所用的概率個數越多,其假設條件的可靠性就越低,條件不可靠又導致結論的可靠性較低。
在決策者看來,先驗行為假設結論的可行性主要體現在所需結果個數和結論的復合階數上。所需結果多,對應的概率個數亦增多,帶來條件和結論的不可靠,故不適用;結果復合階數越多,即伴隨著(x)→(x,p)→((x,p),q)的復合過程,不確定程度在不斷增強,人們不會輕易做出這種假設。因此結論復合階數越高的假設,其可行性越低。
5.2 4種不同先驗行為假設比較分析
表1給出了復合不變性、中值不變性、還原不變性、冪不變性4種不同先驗行為假設,在所需概率個數、所需結果個數以及結論復合階數3個方面的對比。
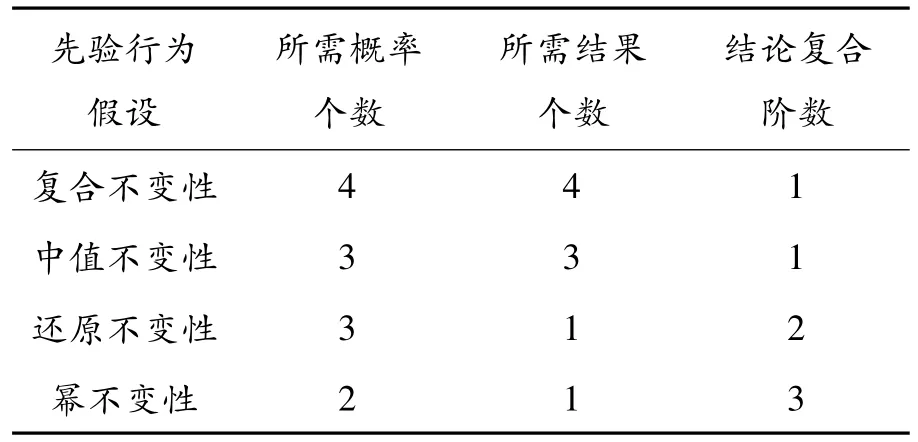
表1 先驗行為假設對比
對比分析可知:Luce把復合不變性發展成為還原不變性,雖然所需結果的個數減少到1個,卻使得其結論增加為二階的復合,可行性降低;Al-Nowaihi和Dhami把還原不變性發展到冪不變性,雖使其所需概率個數減少到2個,但其結果卻要求為三階復合,使得其可行性嚴重降低,且其需要兩步復合,較還原不變性更加繁瑣。因此,還原不變性、冪不變性假設因為其結果的復雜使得可行性降低;復合不變性要求4個結果,并對應4個概率,事實上與其可靠性相比很低。中值不變性結論為一階復合且一步復合,具備了復合不變性的優勢,其所需概率個數和還原不變性所需概率個數相等,可靠性較高。因此本文提出的中值不變性綜合3種先驗行為假設的優點,無論在可行性還是可靠性上都具優勢。
6 結束語
本文就現行的先驗行為假設不能同時滿足較高程度可行性和可靠性的問題,介紹一種稱為中值不變性的先驗行為假設,提供一種推導Prelec概率權重函數的新方法,并得到了更弱條件下滿足中值不變性的定義。通過4種先驗行為假設之間的對比分析,闡述了中值不變性在可行性和可靠性2個方面的綜合優勢,便于決策者采用。其結論對決策者有實際參考意義。
[1] Kahneman D,Tversky A.Prospect theory:an analysis of decisions under risk[J].Econometrica,1979,47(2):263-291.
[2] Tversky A,Kahneman D.Advances in prospect theory: Cumulative representation of uncertainty[J].Journal of Risk and Uncertainty,1992,5(4):297-323.
[3] Prelec D.The probability weighting function[J].Econometrica,1998,66:497-527.
[4] Luce R D.Reduction invariance and Prelec’s weighting functions[J].Journal of Mathematical Psychology,2001,45(1):167-179.
[5] Al-Nowaihi A,Dhami S.A simple derivation of Prelec’s probability weighting function[J].Journal of Mathematical Psychology,2006,50(6):521-524.
[6] Aczel J.Lectures on functional equations and their applications[M].New York:Academic Press,1966.
[7] Bleichrodt H,Kothiyal A,Prelec D,et al.Compound invariance implies prospect theory for simple prospects[J].Journal of Mathematical Psychology,2013,57(3):68-77.
(責任編輯 劉 舸)
Development of Prior Behavior Assumption for Prelec’s Probability Weighting Function
WANG Jin-shana,LI Wei-bingb
(a.Department of Basic Theories;b.No.2 Team of Graduate Management Unit Army Officer Academy,Hefei 230031,China)
We introduce a new prior behavior assumption named mid-value invariance,provide a simpler derivation of Prelec’s probability weighting function,and obtain a weaker condition for definition.We have analyzed and stated its advantages both on feasibility and reliability,so the new conclusion has the reference significance in practice.Thus far,we have four different priori behavioral assumptions all leading to Prelec’s function.
prospect theory;Prelec’s probability weighting function;development of prior behavior assumption;mid-value invariance
C931.1
A
1674-8425(2014)07-0132-05
10.3969/j.issn.1674-8425(z).2014.07.026
2014-03-21
王金山(1962—),男,安徽亳州人,教授,主要從事預測與決策分析方面的研究;通信作者 李偉兵(1990—),男,河南許昌人,碩士研究生,主要從事預測與決策分析方面的研究。
王金山,李偉兵.Prelec概率權重函數先驗行為假設拓展[J].重慶理工大學學報:自然科學版,2014(7): 132-136.
format:WANG Jin-shan,LI Wei-bing.Development of Prior Behavior Assumption for Prelec’s Probability Weighting Function[J].Journal of Chongqing University of Technology:Natural Science,2014(7):132-136.

