課堂教學隨筆
——由軌跡求曲線方程想到的

冉邦恒

（酉陽職業教育中心，重慶 409899）

課堂教學隨筆
——由軌跡求曲線方程想到的

冉邦恒

（酉陽職業教育中心，重慶 409899）

在中學數學解析幾何中，求動點的軌跡方程，既是學習的重點內容，也是所教的難點之一，特別對于中等職業學校的學生來說更是如此，由于知識結構的差異，多數學生是奔專業乘興而來最后卻掃興而歸.但另一方面，學好這部分知識，對中職學生的專業知識的鞏固和專業技能的提升都有極大的幫助.

課堂教學；隨筆；曲線方程

如何確定動點軌跡的方程，怎樣運用解題方法，在數學學習過程中顯得尤為重要.坐標系的選擇是基礎，不同的坐標系，就有著不同形式的方程，同一坐標系下不會因解法不同而有不同的方程.教學中，首先讓學生明白軌跡是具有共同特性的動點的集合，引導學生對于“定點”、“定長”、“定直線”這三“定”的理解（課本上關于圓、橢圓、雙曲線、拋物線方程的建立過程，就是求曲線方程的典范，在教學中必須充分發揮其示范作用）.擬定與三“定”有關的題目，讓學生嘗試建立不同的坐標系，如已知△ABC的一邊為8，周長為20，求頂點A的軌跡方程.其次，掌握教材中求動點軌跡的最主要最基本的五個步驟，即：（1）建系；（2）設點；（3）列式；（4）代換；（5）化簡.無論是自建坐標系，還是已建坐標系，列式與代換是重點，運用不同的知識體系，采取不同的數學手段，由不同的數學表現形式，經過不同的數學處理，最終得出所要的結論，它是數學能力的綜合體現.

一、自建坐標系求方程

例：設動點M與兩定點A，B所在的直線互相垂直，求動點M的軌跡方程.

解法一：以過AB兩定點的直線為X軸，線段AB的中點O為原點，建立直角坐標系，設M（X，Y）為曲線上不與A（-a，0），B（a，0）合的任意一點，由已 知 條 件 MA⊥MB得|MA|2+|MB|2=|AB|2，根據兩點間的距離公式，得

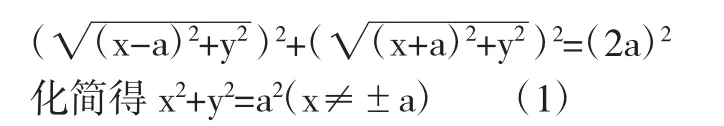
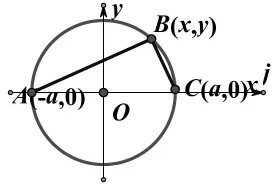
方程（1）即為所求的點M的軌跡方程.

解法二：以通過A和B兩定點的直線為X軸，A為原點，建立直角坐標系，如圖：

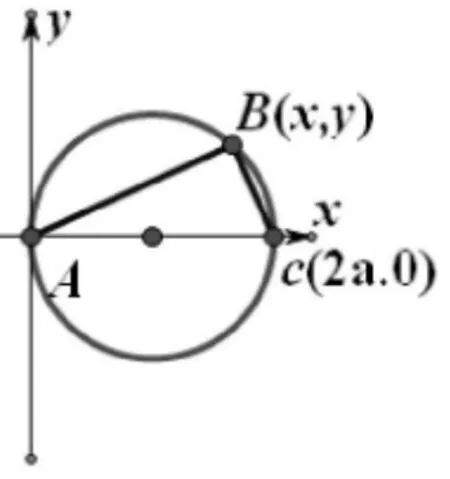
若AB=2a（常量），那么A與B兩點的坐標分別為（0，0）和（2a，0）

設M（x，y）為曲線上不與A，B重合的任意一點，可得|MA|2+|MB|2=|AB|2

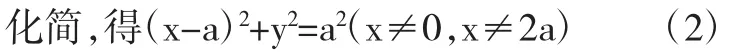
方程（2）也是所求的點M的軌跡方程.

比較方程序（1）（2），可以看出，雖然都是點M的軌跡方程，但由于選擇的坐標系不同，所得的軌跡方程的形式也就不同.方程（1）要比方程（2）簡單，因此，在建立曲線方程時，要注意選擇適當的坐標系，使曲線方程的形式比較簡單.

解法三：坐標系的建立同解法一.

設M（x，y）為曲線上不與A（-a，0），b（a，0）重合的任意一點，由已知條件MA⊥MB KAM·KMB=-1

方程（3）也是所求點M的軌跡方程.

比較以上方程可以看出：在同一個直角坐標系中，用不同的方法求出的同一軌跡的曲線方程是相同的.

二、已建坐標系求方程

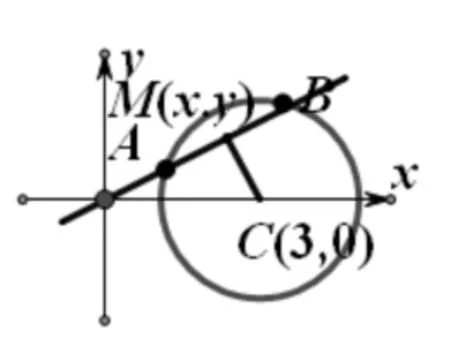
例：過原點的直線與圓x2+y2-6x+5=0相交于A、B兩點，求弦AB的中點M的軌跡方程.

解法一：設動點M（x，y），因CM⊥AB，

化簡得x2+y2-3x=0（x≠3，x≠0）

解法二：在直角三角形OCM中，OM2+CM2=OC2（x2+y2）+（x-3）2+y2=9

化簡得x2+y2-3x=0

所求方程為x2+y2-3x=0

從上兩題看出，求軌跡方程問題，要循序漸進，由易到難，充分利用所學知識，尋求不同的解決方法，在不斷的探索中尋找樂趣.

G633.6

A

1674-9324（2014）07-0237-01

很少愿意動手去畫圖，計算的時候更加不愿意動手，而是利用計算器這個數學工具來代替手算。這些小細節對于學習物理都起到了阻礙的作用。第三，學習物理要經常性地在適當的時間做回顧復習。因為物理的知識點相對來說不會特別多，學生可以在學了一個專題之后，對前面的知識做一個簡單的回顧，不停學習—復習—學習—復習，這樣對知識點的掌握才會更牢固。