定義域優(yōu)先原則在解決函數(shù)問題中的應用

蘇旭景

（河北棗強中學，河北 棗強 053100）

定義域優(yōu)先原則在解決函數(shù)問題中的應用

蘇旭景

（河北棗強中學，河北 棗強 053100）

函數(shù)的定義域具有不可忽視的重要性，所以在研究函數(shù)的相關問題時如值域、最值、單調(diào)性、奇偶性、周期性等，要時刻樹立定義域優(yōu)先的原則。

函數(shù)定義域優(yōu)先原則；最值；參數(shù)范圍；不等式

函數(shù)的三要素是定義域、對應關系和值域。其中函數(shù)的定義域是函數(shù)的根本，因為函數(shù)的定義域如果不同，即使對應關系相同也是不同的函數(shù)。這也是區(qū)分不同函數(shù)的首選條件。函數(shù)的其他性質(zhì)如值域、最值、單調(diào)性、奇偶性、周期性等等無不受到定義域的制約。下面就一些常見易錯題目進行說明。

一、定義域?qū)χ涤颉⒆钪档挠绊?/h2>

例1 已知函數(shù)f（x）=2+log3x（1≤x≤9），求函數(shù)y=[f（x）]2+f（x2）的值域.

解：因為f（x）的定義域為[1，9].所以要使函數(shù)y=[f（x）]2+f（x2）有意義，

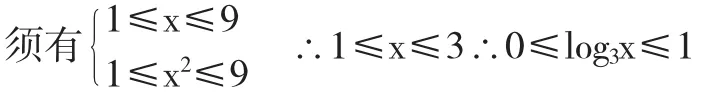
∴當x=3時，即log3x=1時，y的最大值為3.

當x=1時，即log3x=0時，y的最小值為6.

所以函數(shù)y=[f（x）]2+f（x2）的值域為[6，13].

本題學生在做題過程中忽略所求函數(shù)的定義域，認為所求函數(shù)的定義域與原函數(shù)的定義域相同得到錯解。

二、定義域?qū)握{(diào)性的影響

例2 函數(shù)y＝log（2-x2+3x-2）的單調(diào)增區(qū)間是_______；

解析：由-x2+3x-2＞0，得1＜x＜2，

所以函數(shù)y＝log（2x2-3x+2）的定義域為（1，2）．

又y＝log2（tt＞0）是增函數(shù)，

t＝-x2+3x-2在（1，）上是增函數(shù)，

所以函數(shù)y＝log2（-x2+3x-2）的增區(qū)間為（1，）．

本題學生在做題過程中忽略函數(shù)的定義域，直接求真數(shù)即二次函數(shù)的單調(diào)區(qū)間等效成所求函數(shù)的單調(diào)區(qū)間，導致所求單調(diào)區(qū)間超出了函數(shù)的定義域而犯錯。

三、定義域?qū)χ芷谛缘挠绊?/h2>

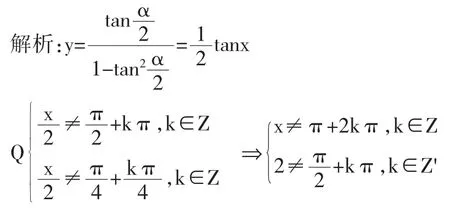
故答案選C.

本題學生在對原函數(shù)變形前未考慮函數(shù)的定義域，使得函數(shù)的定義域前后發(fā)生改變，從而得到錯誤的答案。

四、定義域?qū)ζ媾夹缘挠绊?/h2>

所以函數(shù)f（x）是奇函數(shù).

點評：這樣做忽視定義域的對稱性，由定義可知，函數(shù)具有奇偶性的必要條件是對于定義域內(nèi)的任意一個自變量x，必須f（-x）＝f（x）或f（-x）＝-f（x），且-x屬于定義域時，才有意義，即定義域必須關于原點對稱.

正解：因為f（x）的定義域為{x|x≠-2}，所以函數(shù)f（x）是非奇非偶函數(shù).

事實上，如果一個函數(shù)的定義域不關于原點對稱，那么它一定是非奇非偶函數(shù)！因此，我們在判斷函數(shù)的奇偶性時強調(diào)要有定義域“優(yōu)先意識”.

五、定義域?qū)?shù)范圍問題的影響

例5 設定義在[-2，2]上的偶函數(shù)f（x）在區(qū)間[0，2]上單調(diào)遞減，若f（1-m）＜f（m），求實數(shù)m的取值范圍．

解析：∵f（x）是偶函數(shù)∴f（－x）＝f（x）＝f（|x|）

∴不等式f（1－m）＜f（m）?f（|1－m|）＜f（|m|）

又當x∈[0，2]時，f（x）是減函數(shù)，

本題學生忽略函數(shù)的定義域[-2，2]，使得所列條件不足，從而得到錯誤的答案。

例6 已知函數(shù)f（x）=loga（2-ax）在[0，1]上是減函數(shù)，則a的取值范圍是（ ）.

A.（0，1） B.（0，2） C.（1，2） D.（2，+∞）

解：由題意知a＞0且a≠1，所以t=2-ax為減函數(shù).

又因為f（x）=loga（2-ax）在[0，1]上是減函數(shù)，

通過上述幾個例子，說明函數(shù)的定義域的不可忽視重要性，所以在研究函數(shù)的相關問題時如值域、最值、單調(diào)性、奇偶性、周期性等，要時刻樹立定義域優(yōu)先的原則，才能避免出現(xiàn)錯誤。

G633.6

A

1674-9324（2014）07-0246-01