動態三次指數平滑法及應用實例

周炳飛

(福州職業技術學院，福建福州 350108)

動態三次指數平滑法及應用實例

周炳飛

(福州職業技術學院，福建福州 350108)

傳統的指數模型多用于處理線性趨勢的時間序列，本文在此基礎上建立了可以處理非線性時間序列數據的動態三次指數平滑模型。以擬合值與源數據誤差的平方和為評價指標，通過使得該指標最小來計算最優時間序列系數，建立三次動態指數平滑模型。評價指標類似于評價函數，對模型自動評價，從而提高模型的適應能力，提高模型的計算精度。通過對實際時間序列的分析，進一步證明通過誤差評價指標評價的方法建立的動態指數平滑可以降低誤差，使預測更加精確。

三次指數平滑；誤差平方和；上證指數

移動平均法和BP濾波法主要用在時間序列有明顯季節波動和趨勢變動的情形.但在實際應用的過程中，時間序列數據(如股票數據)不具有明顯的季節波動和趨勢變動.對于這樣的數據一般采用非線性趨勢的時間序列處理方法進行處理.

線性指數平滑處理時間序列數據容易理解和接受，處理方便快捷，應用領域廣，因此在金融等眾多領域被廣泛采用.通過對眾多預測方面的文章的統計和研究表明，指數平滑法的使用次數非常多，且預測的精度高，適用范圍廣，被眾多工程和研究人員采用，并取得了不少有用的研究成果.基于這種事實指數平滑法以及在這種思想基礎上的預測方法的研究的重要性也是不言而喻的.但是再好的方法也總是存在一定的缺點，通過對缺點的分析以及對優點的吸取，我們發現采用三次指數平滑法能夠使預測更加準確.其主要優點是需要的信息量容易接受，但該模型本身有一個嚴重的缺陷，即參數的靜態性.參數的靜態性主要體現在平滑參數自始至終是一個常數，在實際預測過程中，容易使結果誤差偏大，甚至嚴重失真.為此，本文在分析三次指數平滑模型缺陷的基礎上，建立了三次動態指數平滑模型，并將其用來對上證綜指進行預測.

1 指數平滑法的演變過程

1.1 一次指數平滑建立的模型

一次指數平滑也叫單指數平滑，在時間序列數據沒有季節周期特點，也沒有明顯的遞增遞減趨勢時，采用一次指數平滑模型往往可以取得較好的預測效果.它屬于在常數均值上的隨機游走過程，具體的計算方法如下：

st=αyt+(1-α)st-1,0≤α≤1,t=2,3,…,T.

(1)

其中s1=αy1，α為平滑因子，α越小，st越平緩.重復迭代，可以得到

(2)

通過(2)可以知道預測值是對過去值的加權平均，且是以指數的形式展開的，具有這種特點的方法叫做指數平滑法.雖然在局部類似于隨機游走過程，但一次指數平滑法的預測序列其預測值都是固定的常數，這個固定的常數為sT+k=sT，T是時間序列的最終點.它可以認為是該時間序列最終達到這個值，并不再改變.

1.2 二次指數平滑的定義和特點

二次指數平滑又叫雙指數平滑，它是在一次指數平滑的基礎上演變而來的，它通過對指數進行兩次平滑得到.可以通過對一次指數平滑再進行一次類似的平滑得到二次指數平滑的定義表達：

(3)

二次指數平滑模型的預測如下：

(4)

1.3 三次指數平滑模型

如果對二次指數平滑再進行多次平滑，既可以得到高層指數平滑，這里主要研究三次指數平滑，即僅對二次指數平滑再進行一次平滑就可以得到三次指數平滑.它是以多項式的形式表達的，因此無論從系數的計算還是推導形式的方式都更復雜.但是其精度也進一步得到了提高，更主要的是，一次和二次指數平滑主要用在線性形式，對于非線性情況的適用性大打折扣，而三次指數平滑法除了繼承一次、二次的優點外，應用領域進一步擴大，可以適用于非線性情形，對非線性趨勢也可以做出精準的預測.

設{yt}為時間序列的觀測值，下面對三次指數平滑模型進行介紹，其表達式如下：

(5)

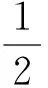
(6)

m為預測超前期數，at,bt,ct均為預測參數.

通過對指數平滑的參數分析可知，指數平滑模型的參數一點確定，它就不再改變，但在實際應用過程中，當時間序列變化比較大時，參數固定往往影響模型的精度，從而使模型的適應性下降，且平滑的初值也比較難確定.針對這種情況引入動態指數平滑模型，使預測精度提高，可靠性也進一步加強.

2 動態三次指數平滑

2.1 動態三次指數平滑模型的建立

將(5)式展開后可以得到：

(7)

(8)

將(8)式中的三個方程進行遞推，則可以得到

(9)

(10)

(11)

2.2 模型精度的評價函數

根據模型精度的要求的不同，評價模型的指標也不一樣，常見的指標有平均絕對誤差(MAE)、平方和誤差(SSE)和均方誤差(MSPE)等.為了計算的方便，利用現有的數學性質，本文采用平方和誤差(SSE)，這樣就可以利用誤差函數在模型初始值已知的前提下求出最優的平滑系數.(12)式即為在平方和誤差平均函數的基礎上，求出動態參數的模型.

(12)

3 應用實例——上證綜指的預測

上證綜合指數數據沒有明顯的趨勢和季節性特征，本文分別用傳統的三次指數平滑模型對上證指數進行模擬和預測，并將誤差進行比較.本文選用2013.5.1-2013.7.29之間的上證指數進行模型應用和比較，取前兩期數據為初始值，對于傳統的三次指數平滑模型平滑參數分別取0.2、0.5、0.6、0.7進行模擬和預測，原始觀測值和指數平滑法的結果如圖1所示，原始數據和三次動態指數平滑法的結果如圖2所示.

圖1 原始觀測值和指數平滑法結果

圖2 原始數據和三次動態指數平滑法結果

對比項傳統三次指數平滑模型動態三次指數平滑模型α0.20.50.7動態平滑系數MSE631.241308.7253.0823.68325

通過對比分析可以看出，對于變化復雜的股票指數，傳統的三次指數平滑模型由于自始至終采用一個參數，所以精度不高.而動態三次指數平滑模型因相關參數隨著時間的變化也在不斷地更新，模型整體處于一種比較優良的狀態.因此，本文結果比傳統的三次指數平滑模型要優良，從誤差項就更能反映這一點.

[1]高鐵梅.計量經濟分析方法與建模[M].北京：清華大學出版社,2006.

[2]吳德會.動態指數平滑預測方法及其應用[J].系統管理學報,2008(2):151-155.

[3]李穎,賈鳳亭.動態三次指數平滑優化模型在遼寧省人均生產總值預測中的應用[J].硅谷,2009(23):152-153.

[4]徐大江.預測模型參數的指數平滑估計法及其應用的進一步研究[J].系統工程理論實踐,1999(2):25-30,43.

[5]張秀英.考試作弊行為的經濟博弈分析[J].東北師大學報:哲學社會科學版,2006(5):156-160.

Dynamic Three Exponential Smoothing Method and Its Application

ZHOU Bing-fei

(Fuzhou Polytechnic, Fuzhou Fujian 350108,China)

Traditional exponential model is usually used to handle the linear trend of time series. In this paper the model is built up based on the nonlinear dynamic three exponential smoothing model of time series data. To fit the square error value and the source of data for the evaluation and by making the minimum index to calculate the optimal time series, the three dynamic exponential smoothing model is set up. Evaluation index is similar to the evaluation function, the automatic evaluation of the model, so as to improve the adaptability of the model and the calculation accuracy of the models. Through the analysis of actual time series, it further proves that dynamic exponential smoothing established through error evaluation index can reduce the error of the prediction so as to make it more accurate.

exponential smoothing; error sum of squares; SSE composite index

2013-11-15

周炳飛(1957- )，男，福建福州人，福州職業技術學院講師，從事數理統計、應用概率研究。

O211

A

1008-178X(2014)01-0010-04