一類PM2.5受風力等因素影響的倉室模型
丁本艷 張利群
(臨沂大學理學院,山東臨沂 276005;山東師范大學數學科學學院,山東濟南 250014)
一類PM2.5受風力等因素影響的倉室模型
丁本艷 張利群
(臨沂大學理學院,山東臨沂 276005;山東師范大學數學科學學院,山東濟南 250014)
通過與倉室模型相聯系,研究在某種特定的情況下,風力、溫度、濕度對PM2.5的影響,并通過微分方程的相關理論分析,給出這些因素對PM2.5的影響關系。
空氣污染;PM2.5;倉室模型;拉格朗日變易法
空氣污染問題是全世界普遍關注的問題,PM2.5是指空氣中直徑小于等于2.5微米的顆粒物,也稱細顆粒物,含量越高就代表空氣污染越嚴重。細顆粒物指數已經成為一個重要的測控空氣污染程度的指數。到2010年底,除美國和歐盟一些國家將細顆粒物納入國標并進行強制性限制外,世界上大部分國家都還未開展對細顆粒物的監測。我國對PM2.5的研究起步比較晚,2011年1月1日首次對PM2.5的測定進行了規范,2013年才開始有比較完整的數據記錄,而且系統尚不規范,因此對PM2.5研究的意義較大。
倉室模型主要運用在研究傳染病傳播等問題上,并取得了豐碩的成果。本文運用倉室模型研究PM2.5的傳播問題,并結合微分方程的相關理論,對影響PM2.5的風力、溫度、濕度等因素進行定性分析。此模型中主要考慮假定的因素,其余的因素假設影響很小,可以忽略,其中對風力分析的時候也考慮一個特殊的風向,比如從西往東吹,對相鄰的三個區域進行分析。
1 模型的建立
為了描述某地區PM2.5的發生和演變,取G,S,X水平方向上的三地,設風從西往東吹,來研究在不考慮其他因素的情況下,風力、濕度和溫度以及左右兩地對其PM2.5的影響,建立模型,其他的風向也可做類似討論。在假設相應的變量系數后構造如下倉室模型:

其中G,S,X分別表示甲地、乙地、丙地的PM2.5。結合倉室模型得到相關的微分方程如下:
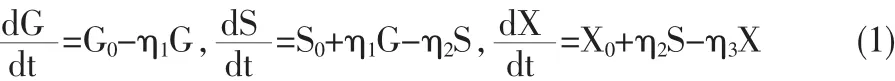
其中,G0=(m1+v1)(α1-α2),S0=(m2+v2)(β1-β2),X0=(m3+v3)(γ1-γ2)。各參數的含義如下:mi≥0,(i=1,2,3)表示G,S,X三地的溫度對PM2.5的有效作用率,vj≥0,(j=1,2,3)表示G,S,X三地的濕度對PM2.5的有效作用率,α1,β1,γ1表示三地在常規狀態下生成的PM2.5的值,α2,β2,γ2表示在常規狀態下PM2.5的擴散值,表示風力對三個地方的有效作用率。
2 模型的分析
由(1)對應的齊次方程組的通解及拉格朗日變易法可得(1)的通解:
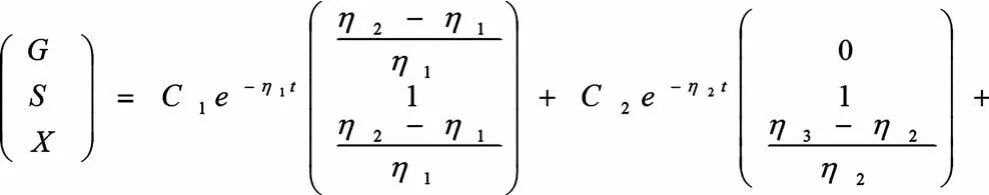


系統(1)中包含各地區內在的溫度濕度的因素,也包括外在的風力因素。運用微分方程的理論,取其中S地的解來分析一下各因素對PM2.5的影響,由上述通解得:
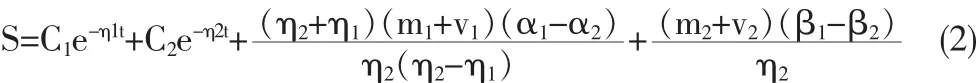
定理1.對于S地區PM2.5的解(2),當t→+∞時,無論k變大還是變小,該地區的PM2.5的值與風力無關,只與自身的溫度濕度有關;但當t在一個小鄰域內時,隨著k的變大,PM2.5的值會變小。
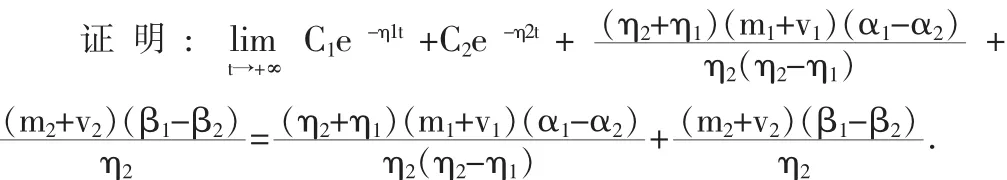
因為S的左邊是單調遞減的指數函數,在t一定時,隨k增大而變小。
定理2.當下列幾種情況至少之一出現時,PM2.5的值S會逐漸減小:1)α1=α2或β1=β2或γ1=γ2時,即各地區的產生與擴散的PM2.5的值相等;2)mi,vi(i=1,2,3)對PM2.5的有效影響率越小時,PM2.5的值會變小。
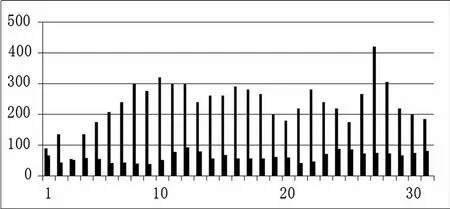
例.比較武漢市2013年1月份和7月份的PM2.5(選擇的目的是這兩個月的溫度、濕度有明顯差異)。
下圖很直觀清楚地反映出它們的PM2.5的差距,1月份大約在200個單位上下浮動,而7月份則在60個單位上下變化,這就說明溫度、濕度等對PM2.5的作用很大,也就是說1月份溫度、濕度對PM2.5相應的有效影響率會較大,7月份較小。
3 結論
綜上可知,在現實生活中,一年有四季,四季的溫度、風力等會有較大的變化。冬季的PM2.5的值會比夏季的PM2.5的值高,而冬季和夏季它們的溫度、濕度和風力是有很大差別的。但是在一個小的時間段內,比如幾天之內,甚至一天之內,他們所對應的相應參數不會有太大變化,比如風力,在短時間內不會有太大變化,那么其主要變化作用的就是溫度和濕度。當然影響PM2.5的產生因素有很多,在此就不予細論。由于我國對PM2.5的認識才剛剛起步,相應的數據收集并不完整,所以當把模型與實際的數據相結合的時候,會有一定的誤差,但是我們相信當有相對完整的數據時,就可以準確地求出各地的有關PM2.5的參數,更加清晰地找出根本所在,并采取相關的措施加以治理。
[1]張芷芬等,微分方程定性理論[M].科學出版社,1997.
[2]馬知恩,周義倉等.傳染病動力學的數學建模與研究[M].北京:科學出版社,2004.
O175
A
1003-5168(2014)04-0184-02
丁本艷(1989—),女,山東萊蕪人,碩士研究生,從事常微分方程定性與分支理論研究。

