基于顯式有限元方法的二維楔形體砰擊壓力系數預報

許蘊蕾

（海軍駐上海地區艦艇設計研究軍代室 上海200011）

基于顯式有限元方法的二維楔形體砰擊壓力系數預報

許蘊蕾

（海軍駐上海地區艦艇設計研究軍代室 上海200011）

利用LS-DYNA軟件對二維楔形體入水問題進行研究。基于顯式有限元方法，選用任意拉格朗日-歐拉算法，建立了包含空氣、水和楔形體的完全耦合的二維有限元模型，研究流場的射流現象與壓力變化情況，預報了二維楔形體砰擊壓力系數，并與已公開發表的模型試驗結果吻合較好，從而為后續砰擊載荷計算提供可靠的方法。

LS-DYNA軟件；二維楔形體；拉格朗日-歐拉算法；砰擊壓力系數

引 言

船舶在海上航行時，經常會遇到惡劣海況，砰擊問題越來越受到學者們的關注。船舶遭受砰擊的瞬時，底部受到巨大的沖擊力，船體的垂向加速度會突然改變并隨即出現高頻振動，嚴重時會造成船體結構的破壞。因此對于船舶設計工作者來說，必須準確預報船體的艏部砰擊壓力。

砰擊問題是一個包含結構、空氣和水三種介質耦合的非線性定常問題。自從Von Karman和Wagner開展研究以來，針對砰擊問題，人們開展了大量的理論、數值和試驗研究工作。Zhao等人［1］研究了邊界元方法，預報了二維楔形體和艏外飄入水砰擊問題，并開展了試驗對比分析工作。駱寒冰［2］采用LS-DYNA軟件，對二維楔形體入水問題進行數值預報，并與Zhao等人的模型試驗結果進行了比較，結果吻合較好。陳震［3］給出二維楔形體入水的基本理論，并采用有限元軟件MSC-Dytran對二維楔形體的入水過程進行仿真模擬，獲得砰擊面上壓力分布以及入水角度對砰擊載荷的影響規律。

本文選用任意拉格朗日-歐拉算法，用拉格朗日網格描述結構，多物質歐拉網格描述空氣和水。采用顯式有限元方法、罰函數耦合算法，來模擬歐拉流體與拉格朗日固體接觸面之間的耦合效應。二維楔形體模型，利用LS-DYNA軟件，對斜升角為10°的剛性楔形入水問題進行仿真模擬，將數值結果與文獻［4］中計算結果進行對比，驗證LS-DYNA軟件在流固耦合分析中的可靠性。同時，本文提出在楔形體入水問題中利用ANSYS前處理實現位移、速度曲線控制的方法，討論了楔形體入水時液面變化情況和噴射區的特點以及流場壓力變化情況，重點討論了斜升角為30°的剛性楔形體入水問題，與Zhao等人的模型實驗結果和理論計算結果進行了對比，得到了砰擊壓力系數。

1 ALE法

ALE法可以處理整個物體有空間的大位移并且本身有大變形等問題，ALE法最早出現于數值模擬流體動力學問題的有限差分方法中。在內部網格的劃分上，吸收了歐拉網格的長處，又不完全相同，ALE法不僅使內部網格單元獨立于物質實體而存在，還可以根據定義的參數在求解過程中適當調整網格位置，避免出現嚴重的畸變。此法可使網格與網格之間的物質流動。與歐拉網格一樣，ALE網格有兩層網格重疊在一起，空間網格可以在空間任意運動，其余與歐拉方法描述一樣，在兩層網格中進行物質輸送。在結構邊界運動的處理上與拉格朗日方法的特點類似，ALE法能夠有效的跟蹤物質結構邊界的運動。

ALE法執行自動重分區時，采用拉格朗日和歐拉兩種算法，包含伴隨重映射的拉格朗日時間步。ALE法可以實現流體-固體耦合的動態分析，可以克服單元嚴重畸變引起的數值計算困難。ALE法先執行一個或幾個拉格朗日時間步計算，此時材料的流動使單元網格產生變形，接著執行ALE時間步計算：

（1）變形后的物體邊界條件保持不變，充分網格內部單元，網格的拓撲關系保持不變；

（2）將變形網格中的單元變量和節點速度矢量輸運到重分后的新網格中，稱為Advection Step。

2 二維楔形體入水問題仿真分析

2.1 建立仿真模型

圖1為楔形體的砰擊物理模型，楔形結構為二維對稱結構，只在z軸方向運動。將靜水面處取為xoy平面，在y軸方向取單位長度。β為楔形體入水角，Ωfluid代表液體歐拉域，Ωair代表空氣歐拉域，ve為入水速度。

圖1 楔形體砰擊計算模型

楔形結構用殼單元描述，空氣和水的流域用六面體歐拉單元表述。在歐拉域中，不同位置的網格大小有變化。越靠近邊界處的網格劃分越粗，而楔形體結構位置附近的網格劃分則較細。選取楔形結構的外側作為流固耦合作用面，楔形體的外表面法向量調整為指向流體。為了形成一個封閉的耦合面，在建模時選取對稱的楔形結構的1/2部分，并將對稱面處的結構單元定義為虛擬單元。楔形體只有一個自由度在z軸方向，模型只劃分一個網格沿y方向，并在該方向的單元表面設置剛性墻邊界條件模擬二維無限大流場。下頁圖2為楔形體部分網格模型。楔形體下落初速度為6.15 m/s。

圖2 楔形體部分網格模型

2.2 狀態方程

本文中流體的壓力采用了線性多項式狀態方程來描述，線性多項式狀態方程表示單位體積內能的線性關系，壓力值由式（1）給定：

式中：C0、C1、C2、C3、C4、C5和C6為常數。如果式中μ＜0，則C2μ2和C6μ2兩項設置為0；其中μ=1/V-1，V表示相對體積。

線性多項式狀態方程可以用于模擬符合γ律狀態方程的氣體，各項系數可設置為C0=C1=C2=C3= C6=0，C4=C5=γ-1（γ為單位熱值律）。

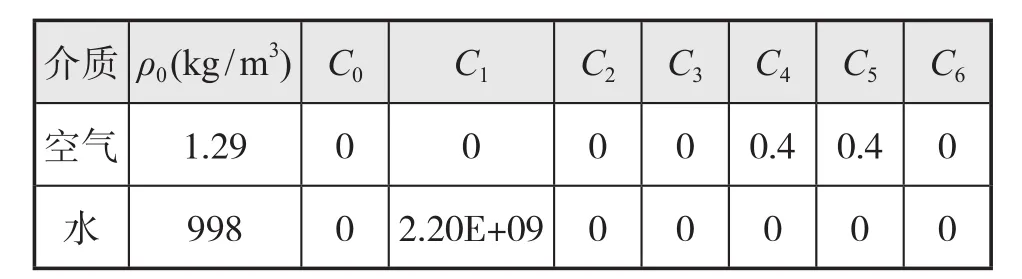
表1 線性多項式狀態方程中空氣和水的參數值

2.3 砰擊壓力系數

基于沖量砰擊理論，楔形面處的砰擊力峰值可以用式（2）表示：

因此，無因次壓力系數k表達式為：

式中： ρ為水的質量密度；V為楔形面在法向的速度分量；k為無因次化的壓力峰值系數。

3 DYNA流固耦合分析要點

3.1 罰函數耦合

為檢查每一個節點對主表面的穿透，用罰函數耦合系數追蹤結構從物質-拉格朗日節點和歐拉流體間的相對位移d。罰函數的物理意義相當于為了限制從節點和主面之間的穿透，在節點和被穿透面之間放置一個法向彈簧，如果不出現穿透，就不進行任何操作。如果有穿透發生，即從節點對主物質表面的穿透，則從節點與被穿透表面之間引入一個大小與穿透深度成正比的較大界面接觸力。罰函數數值的大小不僅影響穿透現象的發生，如果罰函數數值太大，還會使物質產生鋼化現象，物質表面過分剛硬會影響程序計算的穩定。

3.2 剛性體模型速度位移曲線

剛性體模型在顯示動力學分析中具有非常重要的意義。當定義一個剛體后，剛體內所有節點的自由度都耦合到剛性體的質量中心上，每個時間步的節點力和力矩合成為作用在剛性體上的力和力矩。然后計算剛性體的運動，再轉換到節點位移。由于無論定義多少個節點，剛體僅有6個自由度，因此將有限元模型中剛硬部分用剛性體模型定義，可以大大縮減顯示分析的計算時間。

定義剛體模型可約束平移參數和轉動約束參數，所有剛體的加載必須在前處理ANSYS中定義的part號上而不能使用在組件上。在剛體上施加位移條件，相當于在DYNA中定義位移曲線。在前處理ANSYS中定義數組參數位移曲線是將時間間隔和對應的位移值集合在一起。它可以分成兩部分，一部分為時間間隔，另一部分為與時間間隔對應的位移值，定義位移曲線之前，必須首先定義位移曲線的縱坐標和橫坐標值所對應的數組，且其維數必須相同。因此，在計算楔形體以恒定速度入水時，可根據此方法控制楔形體速度保持恒定。

3.3 壓力傳感器

在DYNA中對剛性體模型的單元進行壓力的提取，需要定義壓力傳感器，在輸入文件中定義壓力傳感器位置，這些位置同樣是拉格朗日算符單元所在的位置，壓力傳感器壓力的提取是從流體單元中得到的壓力。

3.4 時間步長尺度

在LS-DYNA中自動選擇的時間步長是基于以下條件的：在一個單位時間步內聲波不允許穿過最小的單元，時間步長也受到全系統剛度的限制，然后與時間步長相關的過大的接觸剛度可能會產生非物理的能量的接觸，時間步長影響了震蕩壓力信號，其作用效果與較高的接觸剛度的作用效果一樣，時間步長的改變對結果沒有明顯的影響。

4 計算結果

4.1 10°斜升角楔形體計算結果比較

文獻［4］中二維剛性楔形體斜升角為10°，該模型采用剛性材料以5.425 m/s的速度等速入水。本文利用LS-DYNA軟件進行仿真，利用前處理ANSYS中施加位移曲線的方式實現等速入水，得到如表2所示，砰擊壓力的理論值與數值解和對應位置本文的仿真值之間的比較結果。本文計算結果誤差較小，計算結果較為可靠。圖3為砰擊壓力時歷曲線。

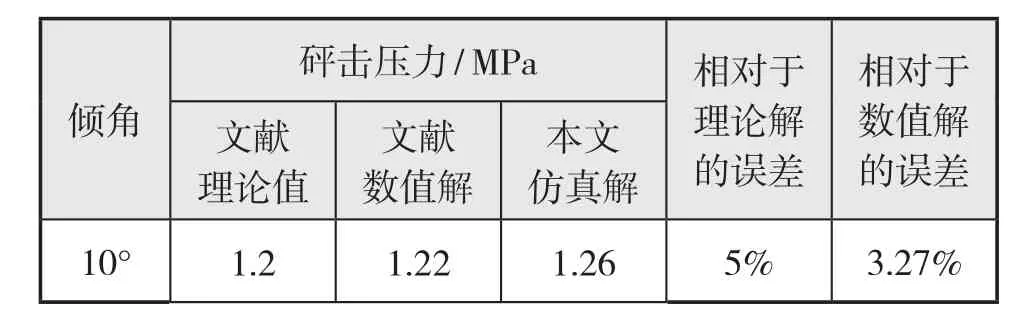
表2 文獻值與本文仿真值之間的比較

圖3 砰擊壓力時域結果

4.2 30°斜升角楔形體仿真模型計算結果

4.2.1 壓力分布

圖4 -圖6顯示了入水砰擊過程中不同時刻的水面飛濺現象。圖7 -圖9顯示流場中壓力分布情況。在該計算模型中并沒有觀察到液體的滲漏現象，表明耦合模擬合理。可以看出，在射流處，砰擊壓力急劇減少，可以忽略不計；在外域水中，離液面升高處越遠，壓力越小。液面分離之前，砰擊壓力的最大值出現在液面升高處。在液面分離之前的入水過程，砰擊壓力的最大值明顯降低，砰擊壓力的最大值出現的位置，將從楔形體底部向上端折角處移動。這是由于仿真楔形體質量較輕，速度下降較快，導致砰擊壓力逐漸減少，也與壓力傳感器得到的壓力相對應，位置越靠上的壓力傳感器測得的壓力最大值越小。

圖4 入水初期

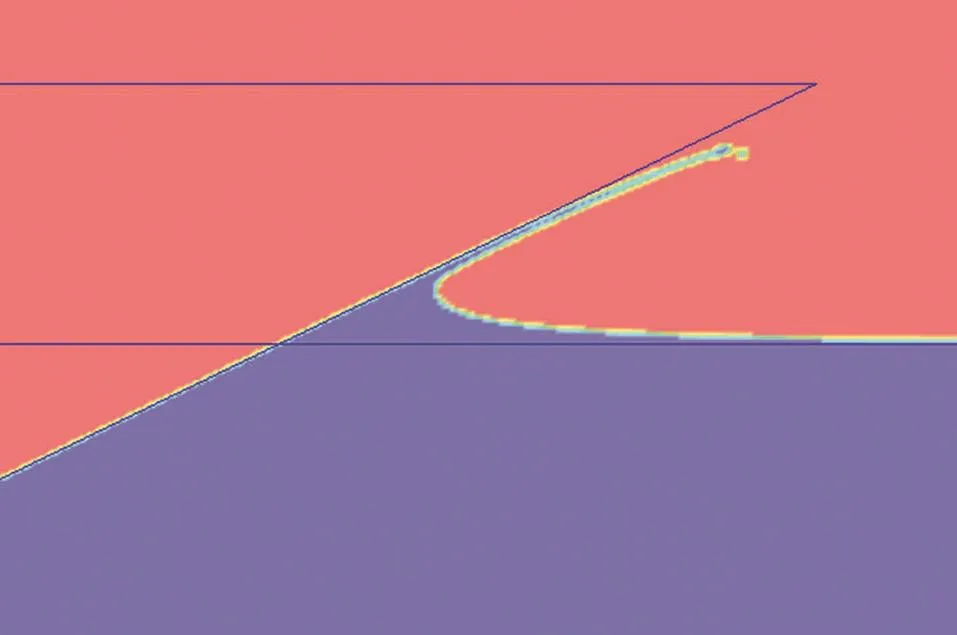
圖5 入水中期

圖6 入水后期

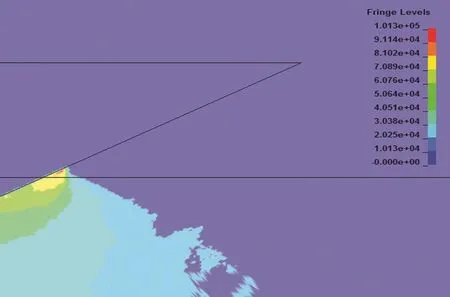
圖7 0.051 s 時流場壓力分布

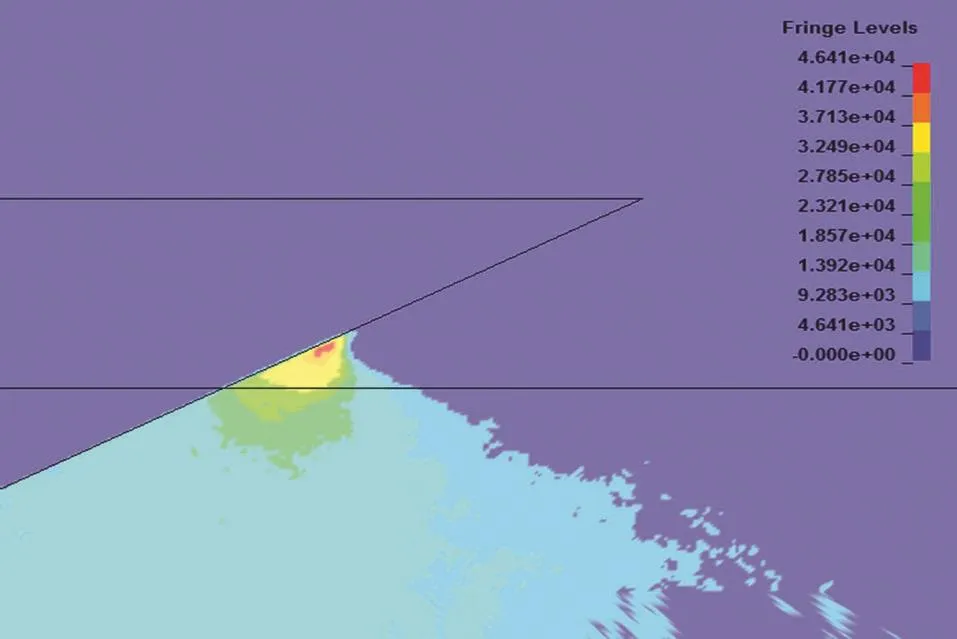
圖8 0.117 s 時流場壓力分布

4.2.2 時域內砰擊壓力曲線

圖10顯示在對應于Zhao等［1］模型試驗中，壓力傳感器位置處的仿真模型壓力傳感器的壓力時歷曲線。最大砰擊壓力的逐漸降低，同時也對應于圖7 -圖9顯示的砰擊壓力最大值的降低。

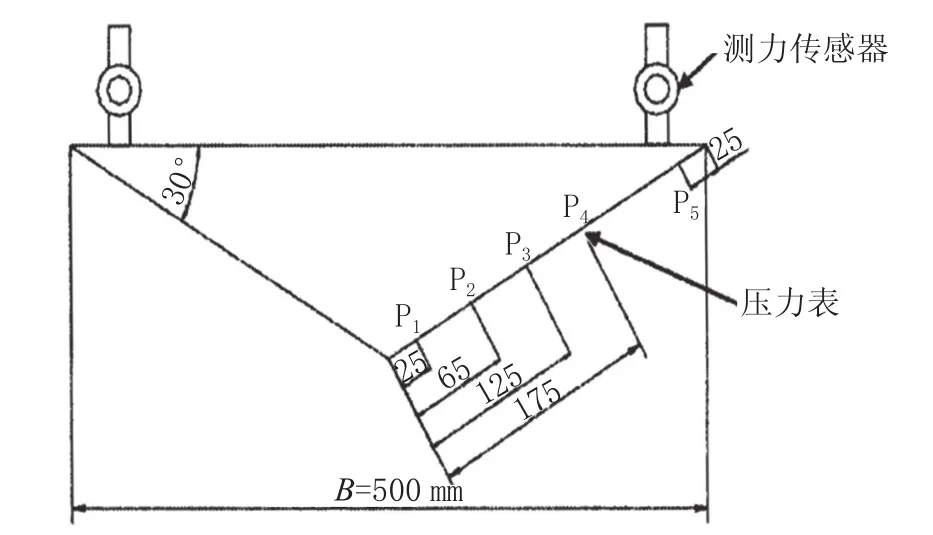
圖10 楔形體入水實驗模型

圖11所示為5個壓力傳感器測得的砰擊壓力時域預報結果。橫坐標是入水時間，5個壓力傳感器位置對應于圖10所示試驗壓力測點位置。

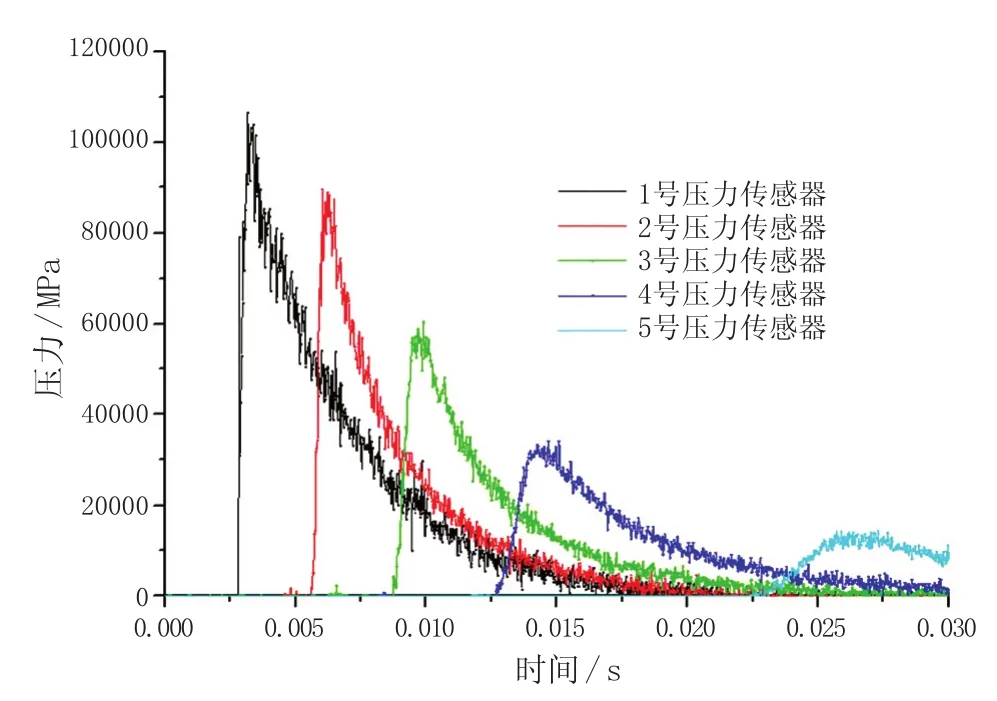
圖11 不同位置砰擊壓力時歷曲線

4.2.3 砰擊壓力系數

文獻［1］中給出不同斜升角楔形體的不同理論算法算得的砰擊壓力系數，對于30°斜升角的砰擊壓力系數曲線如圖12所示。

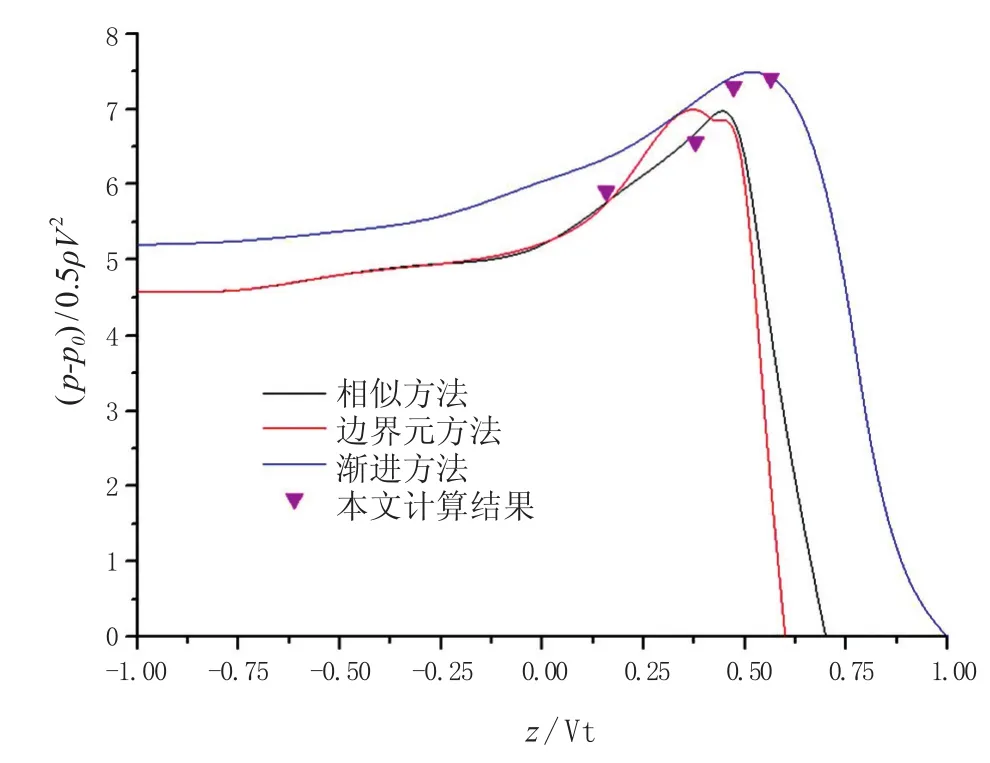
圖12 砰擊壓力空間分布比較

本文計算結果與文獻［1］ 中模型試驗結果吻合較好，圖中所示4個點的數據來源于前4個壓力傳感器。其中，文獻［1］ 給出的理論計算結果是樣條曲線的形式，是由于理論計算中選取計算點數目較多，將一系列計算點結果進行曲線擬合，便得到圖12中的計算結果。

本文利用LS-DYNA軟件進行仿真模擬，考慮到計算時間問題，選取4個點的結果進行比較，因此本文計算給出的結果是獨立點，這些獨立點的計算結果與理論值吻合較好。其中文獻［1］ 給出的結果中，對縱坐標做了無因次化處理，Z是楔形體液面距離楔形體底部的垂向高度，V表示楔形體在入水不同時刻的垂向速度。在砰擊過程中，LS-DYNA預報的砰擊壓力系數與試驗值吻合非常好，反映顯式有限元技術在預報二維剛性體砰擊問題上的可靠性以及本文所采用仿真方法的合理性。

5 結 論

本文采用LS-DYNA軟件，基于顯式有限元方法，采用任意拉格朗日-歐拉算法和罰函數耦合算法，針對文獻［1］ 中楔形體入水砰擊試驗結果以及理論計算結果，建立二維剛性楔形體模型，展開砰擊壓力系數預報工作。預報的10°楔形體砰擊壓力值與文獻［4］中吻合較好，驗證了LS-DYNA在二維楔形體入水仿真中比較可靠。

文中重點分析與Zhao等［1］楔形體入水砰擊實驗相同30°斜升角的楔形體入水模型，得到不同測點的砰擊壓力時域分布以及求得砰擊壓力系數，并與其理論推導結果進行比較，與模型試驗以及理論推導結果吻合較好。預報的砰擊壓力結果可正確描述入水砰擊的整個過程（包括入水初期、入水中期的砰擊過程階段）。LS-DYNA有效預報了砰擊壓力在楔形體表面的時間、空間分布，合理反映出砰擊過程的射流以及內域和外域中的壓力分布，為后續計算砰擊壓力提供了砰擊壓力系數求解的方法。

［1］ ZHAO R，FALTINSEN O M.Water entry of twodimensional bodies［J］. Journal of Fluid Mechanics，1993，246：593-612.

［2］ 駱寒冰，吳景健，王珊，等.基于顯式有限元方法的二維楔形剛體入水砰擊載荷并行計算預報［J］.船舶力學，2012，16（8）：907-904.

［3］ 陳震，肖熙.二維楔形體入水砰擊仿真研究［J］.上海交通大學學報，2007，41（9）：1425-1428.

［4］ AQUELET N，SOULI M，OLOVSSON L. Euler-Lagrange coupling with damping effects：Application to slamming problems［J］.Computer methods in applied mechanics and engineering，2006，195（1-3）：110-132.

Slamming pressure coef fi cient prediction for water entry of 2D wedge body with explicit fi nite element method

XU Yun-lei
(Representative Of fi ce of Naval Warship Design & Research, Shanghai 200011, China)

The water entry of a two-dimension wedge body has been studied by LS-DYNA software. Based on the explicit finite element and Arbitrary Lagrangian-Eulerian (ALE) algorithm, it builds up a two-dimension coupling fi nite element model including air, water and wedge, studies jet fl ow and pressure change, and predicts the slamming pressure coef fi cient of the two-dimension wedge body. The results are consistent with the published model test results, which can provide the reliable method for calculating of the slamming pressure coef fi cient.

LS-DYNA software; 2D wedge body; Arbitrary Lagrangian-Eulerian (ALE) algorithm; slamming pressure coef fi cient

U661.44

A

1001-9855（2014）03-0042-06

2014-02-18 ；

2014-04-16

許蘊蕾（1981-），女，碩士，工程師，研究方向：船舶總體設計。