深水鉆井船動力定位時域仿真分析

田華勇 張海彬

（中國船舶及海洋工程設計研究院 上海 200011）

深水鉆井船動力定位時域仿真分析

田華勇 張海彬

（中國船舶及海洋工程設計研究院 上海 200011）

時域仿真分析是獲得動力定位控制精度的必要手段。文中進行了SIMO軟件理論和應用方面的研究，基于SIMO軟件建立動力定位能力時域仿真分析流程；以深水鉆井船為算例，通過動力定位系統控制參數和Kalman增益參數的調整，獲得較好的計算結果，并進一步分析了控制參數的不同取值對動力定位能力的影響。文中建立的深水鉆井船動力定位能力仿真分析流程可以為工程實踐提供參考。

深水鉆井船；動力定位；時域分析；Kalman濾波；最優控制理論

引 言

在深海作業的船舶或平臺必須配備動力定位系統，通過頻域分析我們可以得到動力定位系統的總功率利用曲線和抗風能力曲線，其結果是在靜態平衡的基礎上計算得出［1］。然而，船體在海洋環境中所受風、浪、流等載荷不斷地變化，動力定位系統對動態載荷的反應以及對船體的控制效果是實際工程應用更為關注的［2-3］。

由于深海自然環境條件惡劣，定位難度更大，而海上鉆井作業對鉆井船位置偏移的控制要求苛刻，漂移控制應該滿足隔水管柱上下球接頭所允許的偏移角范圍內。一般正常鉆井作業允許接頭在3°內活動，即漂移范圍為（水深-導管柱頭高度-防噴器組高度）×tg3°，如果井內無鉆具時，允許球街頭在10°內活動，即漂移范圍為（水深-導管柱頭高度-防噴器組高度）×tg10°。動力定位過程中環境載荷的改變、控制系統對定位信息的處理以及推力系統的響應等三方面只能在時歷分析中加以考慮。在工程設計階段，動力定位精度是比較重要的技術指標，而時域分析是獲得動力定位控制精度的必要手段，所以對鉆井船在深海環境條件下的動力定位時域仿真分析很有必要。

本文將對時域計算軟件SIMO進行理論和應用方面的分析，建立基于SIMO的動力定位時域仿真分析流程，獲得鉆井船在深海環境條件下的動力定位精度和功率消耗情況。

1 SIMO中動力定位時域仿真分析的理論和應用分析

1.1 SIMO中的時域計算

SIMO是Marintek開發的軟件，廣泛用于計算海洋復式結構物的運動時域模擬和定位能力分析［4］。SIMO中時域計算的本質是求解運動方程，在每個時間步計算船體的非線性運動響應。下面簡要分析如何處理頻域運動方程以用于時域計算。

以正弦運動為例，運動方程一般可以寫成：

式中：M為由頻率決定的質量矩陣；m為船體質量矩陣；A為由頻率決定的附加質量；C為由頻率決定的阻尼矩陣；D1為線性阻尼矩陣；D2為二階阻尼矩陣；f可由決定；K為靜水力剛性矩陣；x為位移向量；q為外載荷向量。

運動可以分解為兩部分，高頻（波頻）部分和低頻部分。同時外載荷也可以分為高頻（波頻）和低頻兩部分。

波頻運動的本質是簡諧運動，運動可以在頻域內進行求解，這要求運動相對波浪而言為線性響應，也就是說二階阻尼矩陣D2為零，且靜水力剛性矩陣K為常數。波頻運動方程在頻域內可寫成：

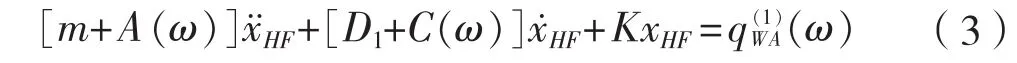
在SIMO進行時域模擬的過程中，高頻運動的頻率ω會進行更新。由于將高頻運動分離出來，低頻運動方程就可以進行時域計算，其動態平衡方程可以寫成：

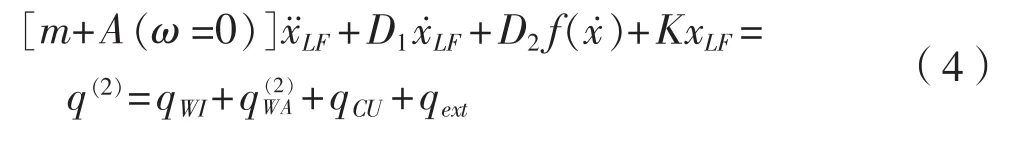
式中：qWI為風載荷為二階波浪誘導力；qCU為流載荷；qext為其他外部力（波浪漂移阻力、來自定位和連接單元的外力等）。

1.2 SIMO中的動力定位計算

動力定位是指通過自動控制保持船體位置和艏向的技術［5］，系統組成包括測量系統、推力系統和控制系統，其中控制系統是核心部分。因為動力定位系統只對船體的低頻運動偏移做出反饋控制，所以需要根據測量結果確定船體的低頻位置信息。位置估計和反饋控制是動力定位比較重要的兩方面。動力定位時域仿真分析指的是模擬船體在動態環境載荷作用下和動力定位系統控制下的運動，為了實現這個功能，SIMO集成了動態環境載荷生成、低頻位置估計、動力定位控制和推力分配等方面的數值計算。

動力定位控制環組成部分和理論基礎概括為：

（1）擴展的Kalman濾波器，以Kalman濾波理論為基礎；

（2）反饋控制器，以最優控制理論為基礎［6］；

（3）推力分配系統，以最優化控制理論為基礎。

SIMO中動力定位系統的模擬流程分列如下：

● 推力分配系統根據總的推力和力矩需求計算每個推進器的推力大小和方向；

● 進行運動方程的時域求解，獲得船體的最新位置；

● 利用Kalman濾波器確定船體低頻運動的位移和速度；

● 與目標位置進行對比，獲得低頻位移的水平偏移量；

● 根據位移的偏移量和船體速度確定總的推力和力矩需求。

1.3 SIMO中的動力定位控制策略

SIMO中提供兩種控制策略［4］，分別為PID控制器和基于Kalman濾波的控制器，因為后者基于現代控制理論，可以解決PID控制器中相位滯后等問題，應用較多，具體理論內容可參考文獻［7］。下面以船體X方向的運動為例來說明基于Kalman濾波控制器的應用流程。這里把SIMO中用于估計船體位置的部分稱作估計器，把反饋控制部分稱作控制器。

SIMO中把船體測量系統的位置測量值與Kalman濾波器估計值的差值稱為過程更新項。估計器中的狀態變量會用過程更新值與Kalman增益的乘積來更新。

式中：xLF和xHF分別表示低頻和高頻運動位移值，這里可以看成先驗估計值，由低頻運動方程和高頻運動方程求得。

接著更新低頻變量和高頻變量：

動速度；這里得到的xLF為后驗估計值，并輸入到控制器中。

緩變載荷FBx的更新為：

在進行下一個時間步計算的時候，高頻運動的頻率根據Balchen［8］來更新。通過估計器的計算，就可以得到每個時刻低頻運動的位置，接著進入控制器的計算。

動力定位的推力需求是通過低頻運動位移偏差的反饋控制和環境載荷的前饋控制得到的，首先通過低頻運動變量得到推力反饋值：

式中：FTx為推力系統作用于船體的推力；和表示速度和位移與目標位置的偏差；表示控制增益矩陣。

在環境載荷作用的情況下，滿足動力定位需求的推力必須加上用于抵消緩變載荷的部分，其中緩變載荷包括估計值和風力測量值，如式（9）所示：

式中：FBx表示緩變環境載荷；FMx表示測量的風載荷。得到推力需求后，SIMO會自動為每個推力器分配推力的大小和方向。

在每個時間步重復從估計器到控制器的計算，就可以完成對動力定位的時域計算。

1.4 SIMO參數的輸入和調整

SIMO中的Kalman增益和控制增益是需要輸入的。Kalman增益值的準確與否直接影響船體低頻運動位置的估計，進而影響動力定位控制精度，而控制增益的取值對于推力系統功率消耗是否最小至關重要。SIMO中給出了用于初始調節的建議值。

控制增益的建議值為：

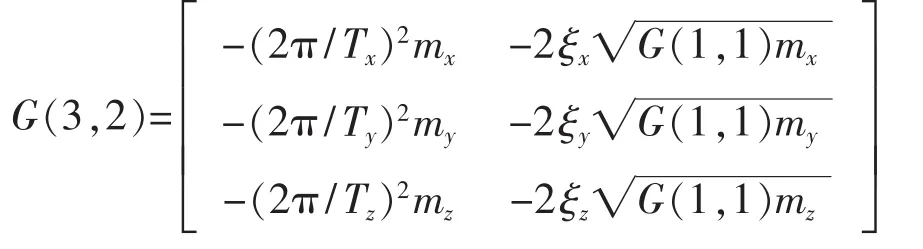
Kalman增益的建議值為：

控制增益和Kalman增益建議值只是用于初始計算。在應用SIMO進行動力定位時域計算時，應在初始值的基礎上，根據初算結果的特點，依據Kalman濾波算法和最優控制的原理對增益值進行調整，以達到比較好的計算結果。可以通過改變Kalman增益值來調整測量值和過程值所占權重［8-9］：當動力定位控制結果不好，并且位置預測結果中出現比較多的高頻成分，這時應該降低和的值，使過程值占到更大的權重。控制增益的取值受系統周期Tx的影響，若系統周期較小，則控制增益較大，由一定的位置偏移產生的推力需求會變大，控制精度會變好，但調整頻率較高，功率消耗較大；若系統周期較大，則控制增益較小，由一定的位置偏移產生的推力需求會變小，控制精度會變差，但功率消耗會變小。

2 動力定位時域分析實例計算

現以“MARIC 10000”號鉆井船（如圖1所示）為例，進行基于SIMO的動力定位時域仿真分析。該船主尺度如表1所述，6個全回轉推力器的布置如圖2所示，其坐標參照表2。

圖1 “MARIC 10000”號鉆井船效果圖

表1 MARIC 10000號鉆井船主尺度

圖2 鉆井船推力器位置示意圖

表2 推力器最大推力與位置坐標值

SIMO中控制參數的設置需要經過多次調整以使控制效果達到理想的狀態。在輸入文件中對動力定位計算的相關設置為：

（1）推力分配策略的選擇與參數設置

選取基于Kalman濾波器的控制器，相關參數為：

（2）時間序列的生成方法選取余弦函數法；

（3）環境條件的設置

風：API風譜，風速為29.3 m/s，風向為200°；浪：JONSWAP雙參數波譜，有義波高5.27 m，譜峰周期12.95 s，浪向為180°；流：定常流，流速0.5 m/s，流向為225°。

在6個推力器正常工作的情況下，計算時間2 048 s，時間步長取0.5 s，對不同案例的計算如下。

2.1 Case 01 以建議值為基礎的初始計算

將控制增益和Kalman增益值取為SIMO的建議值，計算結果如下頁圖3與圖4所示。

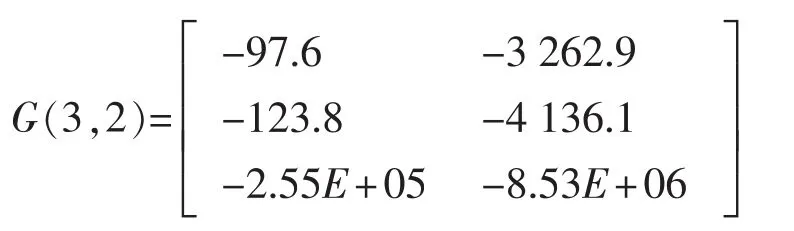
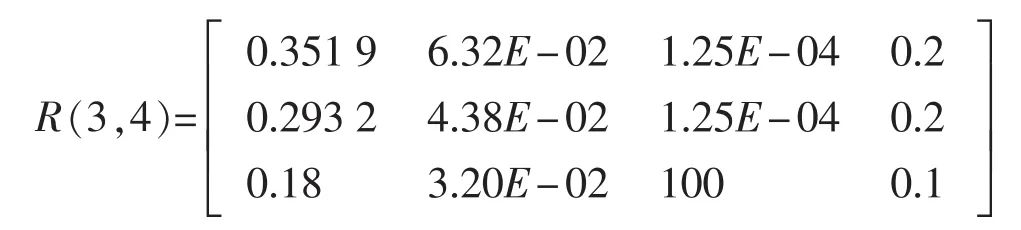
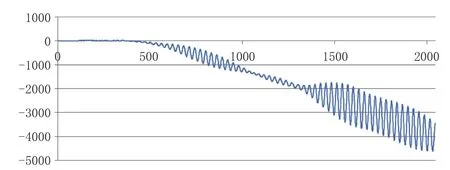
圖3 Case 01 船體 X 方向低頻位移 / m

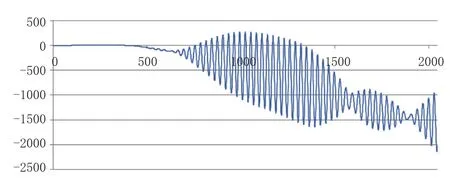
圖4 Case 01 船體 Y 方向低頻位移 / m

2.2 Case 02 降低船體位移和速度的Kalman增益

從Case 01的結果可以看出，對船體的低頻位置估計出現問題，可能是低頻位置和速度的Kalman增益過大所致。現將其減小，控制增益保持不變，緩變載荷依然采用流速估計的方法，具體如下所示。

圖5 Case 02 船體 X 方向總位移 / m

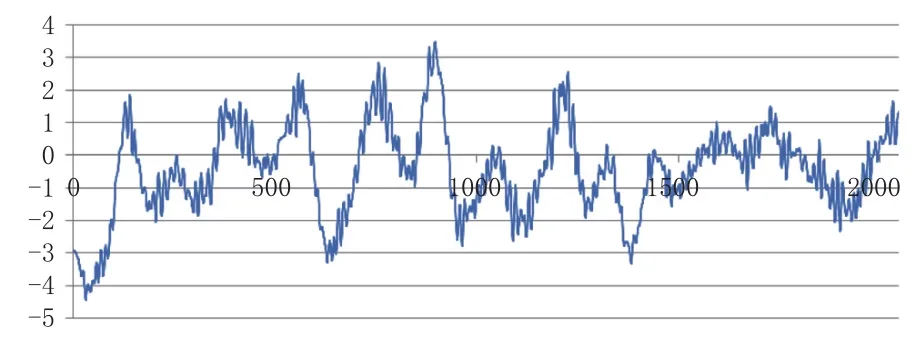
圖6 Case 02 船體 Y 方向總位移 / m

從圖5 -圖6結果可看出，改動之后的動力定位結果明顯得到改善，橫向、縱向的位移和艏向的角度都可以保持在比較小的偏移范圍內。從總位移曲線清晰可見低頻運動和高頻運動疊加后的結果，船體的位置改變主要是以低頻位移為主，高頻運動只是在低頻運動位置的小頻振蕩。進一步可發現船體的初始位置還是偏大，這可能是沒有在控制器中考慮測量風載荷的結果。SIMO在動力定位時域模擬之前，會根據給出的控制增益和環境條件進行靜水平衡計算，由此得到的平衡位置用于之后的時域模擬。

2.3 Case 03 在控制器中計及測量的風載荷

針對Case 02中初始值過大的情況，現通過輸入文件中參數的設置，將風載荷考慮在初始計算中，并選擇低通濾波器，測量風載荷的截斷周期取50 s。保持控制增益和Kalman增益等其他參數與Case 02相同，結果如圖7 -圖10所示。

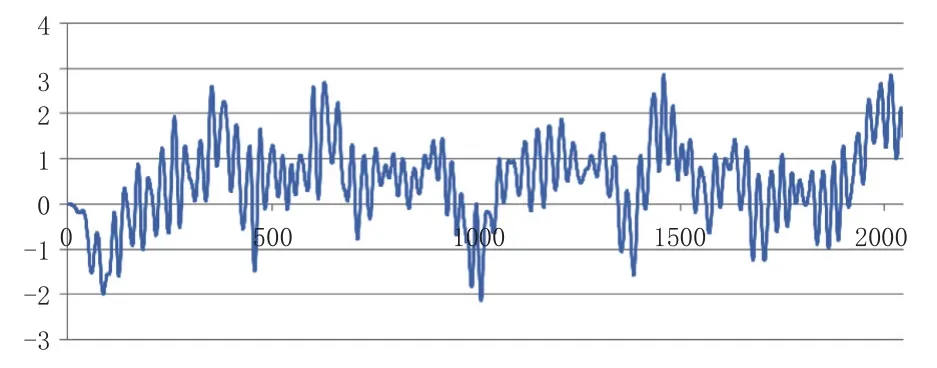
圖7 Case 03 船體 X 方向總位移 / m

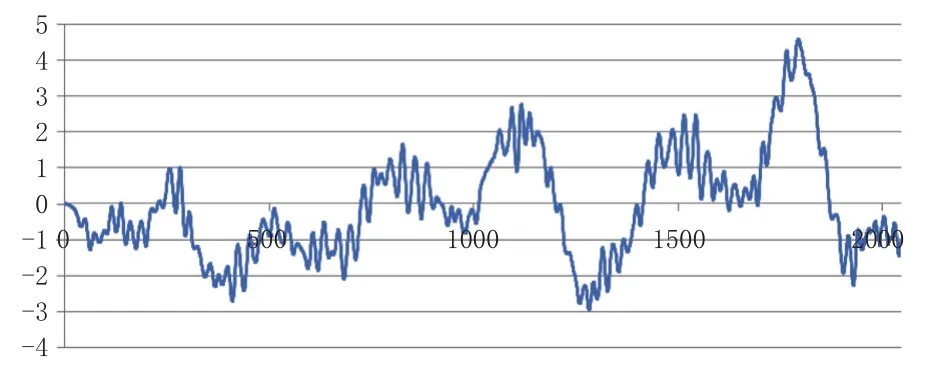
圖8 Case 03 船體 Y 方向總位移 / m

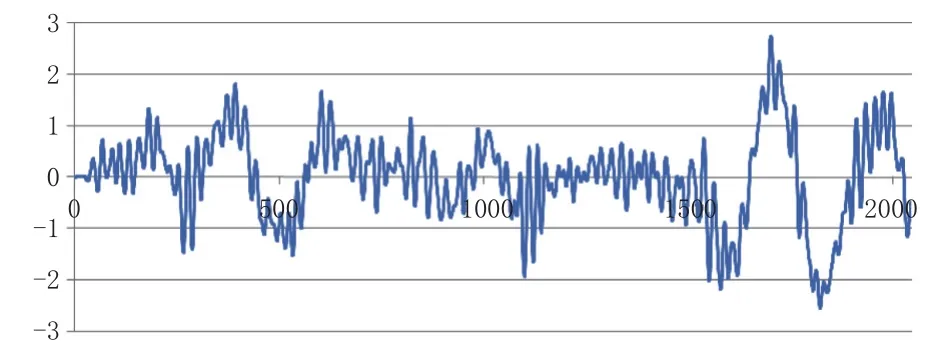
圖9 Case 03 船體艏向偏移角度 / (°)

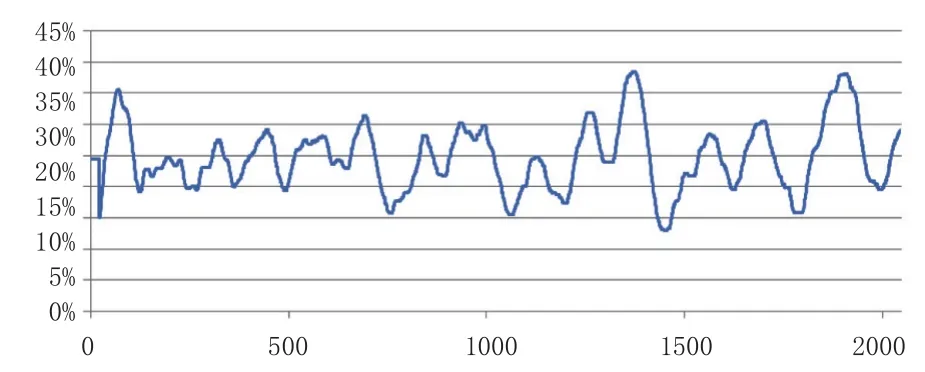
圖10 Case 03 推力系統總功率消耗時歷曲線 / m

從結果中可以看出，初始位置得到很好的改善，這與SIMO中確定初始位置大小的算法有關。因為推力需求通過FTx= FTx-FDx-FMx得出，在初始計算的時候只有環境載荷，總推力應與環境載荷平衡，即等式左邊與等式右邊相等。這里若不考慮風載荷FMx，則等式右邊的FTx值就會比較大，進而導致初始偏差比較大。

通過Case 03的計算，計算結果已經比較理想，圖10也給出總功率消耗的時歷曲線，可見整個推力系統在時域仿真分析中的功率消耗情況。

2.4 Case 04 不同控制增益計算結果的比較

保持Kalman增益等其他參數不變，并將結果與Case 03的結果對比，結果如圖11 -圖14所示。

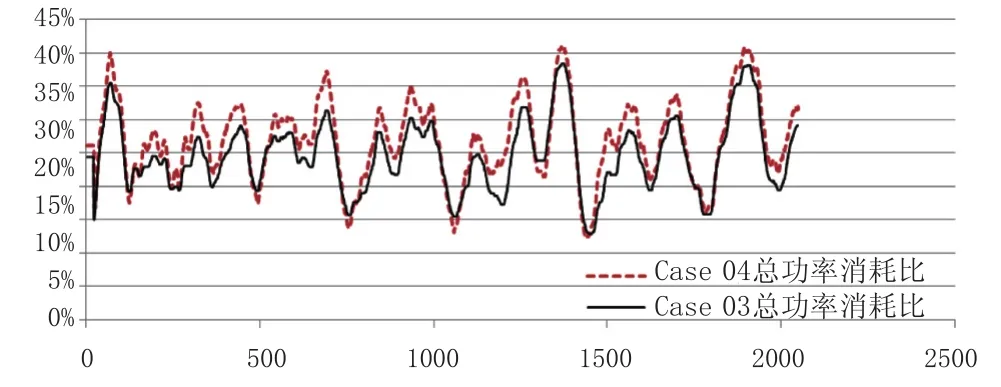
圖11 Case 04 與 Case 03 總功率消耗的對比 /m

圖12 Case 04 與 Case 03 船體 X 方向總位移的對比 / m

圖13 Case 04 與 Case 03 船體 X 方向總位移的對比 / m

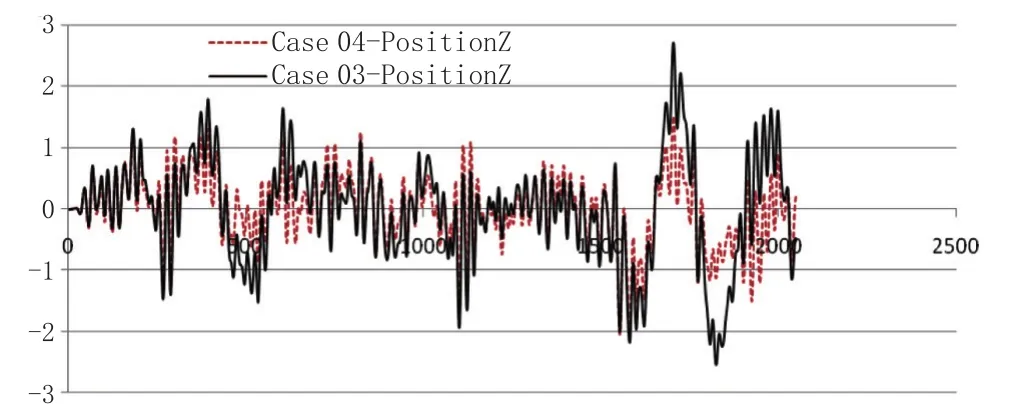
圖14 Case 04 與 Case 03 艏向偏移角度的對比 / m

從對比圖中可以看出，在控制增益G增大之后，船體保持位置所需要的總推力是增大的，但卻有著更好的控制精度，所以提高動力定位系統的控制精度，可能意味著更大的功率消耗。如何在盡可能低能耗的情況下達到盡可能高的定位精度，也是現代動力定位系統發展的一個重要方面。

SIMO中還有其他結果可以進行圖示，比如每個推力器的推力大小和方向的時歷曲線。通過推力的時歷曲線可以分析某一具體推力器在整個動力定位時域模擬過程中推力的提供情況。根據全局坐標系下船體X和Y方向的總位移可以得到船體的運動軌跡，可以更具體地看出在在動力定位系統的控制下船體的運動情況。

圖15 全局坐標系下船體的運動軌跡

3 結 論

本文對SIMO進行理論和應用方面的研究，基于SIMO進行深水鉆井船動力定位的時域仿真分析，經過多次計算總結Kalman增益和控制增益的調整機制，并分析動力定位系統不同參數設置對動力定位精度和功率消耗的影響，形成準確有效的深水鉆井船動力定位仿真分析流程。通過時域仿真分析，可以獲得動力定位精度和功率消耗情況。兩者作為重要的技術指標，可以為實際工程設計提供參考。此外，對于鉆井船這種對動力定位要求較高的船型，可以在本文建立時域仿真方法的基礎上，進一步研究立管或輔助系泊系統等對定位的影響。

［1］ 何進輝.深水鉆井船動力定位能力分析方法研究［D］.中國船舶及海洋工程設計研究院，2012.

［2］ 何進輝，張海彬.動力定位能力分析中的風速和波高關系研究［J］.船舶，2012（2）：11-16.

［3］ 劉學勤，張海彬.深水鉆井船運動性能分析［J］.船舶，2013（3）：12-15.

［4］ Marintek Report. SIMO Theory Manual Version 3.6， rev2［R］. 2009.

［5］ ABS. Guide for thrusters and dynamic positioning systems，Section 3［S］. 1994.

［6］ 顧幸生，劉漫丹，張凌波.現代控制理論及應用［M］.上海：華東理工大學出版社，2008：102-115.

［7］ OLIVIER C. Introduction to Kalman Filter and its use in dynamic positioning systems［J］. Dynamic Positioning Conference， 2003.

［8］ BALCHEN J G. A dynamic positioning system based on Kalman filtering and optimal control［J］. Modeling，Identification and Control， 1980：135-163.

［9］ 喬小國.深水浮式結構動力定位能力動態分析［D］.哈爾濱：哈爾濱工程大學，2010.

Time domain simulation analysis of DP for deepwater drillships

TIAN Hua-yong ZHANG Hai-bin
(Marine Design & Research Institute of China, Shanghai 200011, China)

Time domain simulation analysis of DP is necessary to obtain the control of the dynamic positioning accuracy. This paper carries out the investigation of the theory and application of SIMO software, and performs the time domain simulation analysis of the dynamic positioning by SIMO. Taking a deepwater drillship as an example, the better calculation results can be obtained by the adjustment of DP control parameter and Kalman gain parameter in order to analyze the in fl uence of the different control the parameters of dynamic positioning. The simulation analysis the process of DP for deepwater drillships which is built up in this paper can provide references for practical application.

deepwater drillship; dynamic positioning; time domain analysis; Kalman fi lter; optimal control

U666.11

A

1001-9855（2014）03-0073-07

2013-11-05 ；

2013-12-04

田華勇（1989-），男，碩士，助理工程師，研究方向：動力定位時域仿真。

張海彬（1976-），男，博士，研究員，研究方向：海洋工程總體設計。