基于諧波小波包變換的信號檢測
侯鐵雙, 羅祖軍, 周 有
(西安郵電大學 自動化學院, 陜西 西安 710121)
基于諧波小波包變換的信號檢測
侯鐵雙, 羅祖軍, 周 有
(西安郵電大學 自動化學院, 陜西 西安 710121)
利用二進離散小波變換檢測周期性信號時,由于頻帶間的干擾,微弱成分易被強信號所淹沒,為解決此問題,提出一種基于諧波小波包變換的周期性信號檢測算法。利用諧波小波函數的盒形頻譜結構,根據目標聲信號的特點,選擇合適的分解層數和分析帶寬,由此避免分析頻帶之間的相互干擾。對實測數據的分析結果表明,諧波小波包變換對于低信噪比下的微弱線譜信號成分有一定的增強效果。
水聲信號處理;信號增強;諧波小波包變換
在利用聲納等水聲設備探測目標的過程中,目標輻射信號中的穩定線譜對應于目標上的一些周期性振動源,在一定程度上可用于確定目標的航速、類型,進而實現目標的檢測與分類。
研究艦船的安靜性技術方面一直是各國重點的研究方向并取得很大的成就,使得艦船聲輻射能量有大幅度的下降,與此相反由于海上航運、海洋開發等活動的日益頻繁,使得海洋環境噪聲大幅度增加,這對采用被動技術的目標檢測增加了技術難度,為了降低環境噪聲對信號檢測性能的影響,研究合適的線譜檢測算法很有必要[1]。
檢測水聲目標信號中線譜成分的研究有兩種方法:一是通過對調制的信號進行解調,得到低頻線譜,這種方法主要用于調制比較明顯的情況[2];二是直接對低通濾波后的信號進行變換,得到低頻分量,這種方法用于調制信息不明確的情況[3]。這種方法在一定程度上可以檢測出目標中的某些線譜成分,但是由于目標中的線譜成分可能分布于不同的頻帶內,這種分析方法可能會由于頻帶間干擾的存在使得能量較大的成分完全淹沒能量較低的線譜成分。
諧波小波除具有通常意義下的小波變化的特點外,還具有自身的優勢:小波函數具有明確的數學表達式,無需通過尺度函數迭代的方法構造;不受二進制限制,算法實現簡單[4]。文獻[5]通過算例和工程實例,實現了強噪聲下微弱周期信號的提取,并證明了諧波小波函數在微弱信號的頻域提取能力和精度上明顯優于二進小波。隨后的一些研究也都證明了諧波小波函數在檢測微弱周期性信號中的有效性[6-9]。
本文從諧波小波函數的盒形(Box-like)頻譜結構的性質出發,利用諧波小波包變換實現微弱周期性信號增強,并通過實測信號驗證諧波小波包檢測微弱周期性信號的有效性。
1 諧波小波變換
1.1 諧波小波函數
與通過雙尺度方程構造小波函數不同,諧波小波以小波函數的頻譜為出發點,構造具有盒形頻譜的帶通濾波器作為諧波小波函數的頻譜,其表達式為[4]
(2)
對式(1)做傅里葉逆變換,就得到了諧波小波函數時域表達式
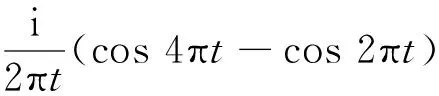
(2)
用變量(2jt-k)替換式(2)中的變量t,這樣就得到了諧波小波ψ(t)的二進函數

(3)
式中j是尺度參數,也稱為小波的分解層,實現對式(2)所表示的ψ(t)壓縮2j倍,k是位移參數,表示分析中心位于t=k。
圖1所示為不同分解層上諧波小波的傅里葉變換的帶寬與幅值關系[4],從中可以看出,隨著j的增大,時間分辨率降低,頻率分辨率增大。

圖1 帶寬與幅值的關系
假設要分析的頻帶范圍為[2πm,2πn](m (4) 此時小波函數在時域的表達式為 (5) (6) 分析式(6),可得到諧波小波函數的正交特性。 (1) 不重合的不同頻帶對應的小波函數相互正交。 (2) 同一頻帶內,不同非零k值對應的小波函數相互正交。 諧波小波函數的這種正交特性更具有普遍適用性,可以更加靈活地實現對信號的分析。利用諧波小波函數系ψm,n(t)構造成L2()的一組正交基,對信號作諧波小波分解時,可以將信號分解成許多無頻段間干擾的獨立頻段,各頻段內微弱的信號由于不受相鄰頻段的干擾而得以準確顯示,這對于微弱信號的檢測具有重要意義。 1.2 諧波小波變換快速算法 設有離散信號f(r)(r=0,1,…,N-1),對f(r)進行傅里葉變換得到傅立葉系數 (7) 根據傅里葉變換的性質,有 (8) 并且,N個傅里葉系數中,除F0與FN/2為實數外,其余一般均為復數。 假設相應的小波系數為as(s=0,1,…,N-1),由于小波系數類似于傅里葉系數,因此有 aN-s=as(s=1,2,…,N/2), (9) 并且除a0和aN/2外,其他系數一般為復數。 由圖1可以看出,第j層中,2j個小波系數a2j+k(k=0,1,…,2j-1)對應于信號f(r)的傅里葉系數F2j+k(k=0,1,…,2j-1)。j層的第一個小波系數為a2j,具有1/2j的常譜密度,因此它對傅里葉系數Fm(2j≤m≤2j+1)的貢獻為a2j/2j。j層的第二個小波系數為a2j+1,與上一個小波相比有1/2j平移,因此它的傅里葉變換也就比上一個小波有e-iωk/2j的偏移量,由于Fm對應于頻率ω=2πm,因此a2j+1對Fm的貢獻為a2j+1e-i2πm/2j/2j。將k=0,1,…,2j-1的所有貢獻組合,得到 (10) 此式即為傅里葉系數與諧波小波系數之間的關系式。用n=2j和s=m-n對式(10)做變量代換,對于s=0,1,…,n-1有 (11) 以16個采樣點的實信號為例,得到圖2所示的小波系數計算示意圖[4]。結合以上分析及圖2可知,諧波小波系數可以通過對信號的傅里葉系數進行傅里葉逆變換得到,從而使得諧波小波相對于二進小波具有計算速度上的優勢。諧波小波在許多領域都有應用[5-8]。 圖2 16序列的實信號的諧波小波算法 基于傅里葉的諧波小波分解為諧波小波變換提供了快速算法,而有些情況下,需要對信號的高頻部分得到與低頻部分同等的分析效果,此時難以用小波變換處理,而小波包變換正好可以處理這類問題。 設第j層上各小波的分析帶寬為 B=fh/2j-1, (12) 待分析頻帶的上、下限分別為 m=sB,n=(s+1)B (s=0,1,…,2j-1)。 (13) 諧波小波包分解的頻域分布如圖3所示。隨著對信號分解的不斷深入,諧波小波包{ψm,n(t)}就實現了信號整個頻帶的細化,直到達到分解要求為止。由圖可以看出,我們可以根據對信號分析的需要選擇感興趣的頻段,進而對相應頻帶進行小波包分解,并利用小波系數對信號進行重構。 圖3 諧波小波包分解的頻域分布 利用諧波小波包進行信號分析時,根據信號的特點可以很容易地選擇合適的分解層數j和分析帶寬B。由于沒有計算小波包系數Wm,n,k的快速算法,不妨考慮采用循環卷積算法來求解。 為驗證諧波小波包檢測信號中微弱線譜成分的效果,將諧波小波包變換對海上實驗所測得的某艦船的通過特性數據進行分析。對于待分析信號取采樣頻率fs=2 000 Hz,根據式(12)和式(13)確定信號的分析帶寬B以及需要分解的層數j。取分解層數j=4,則分析帶寬 圖4至圖11為對某艦船輻射聲信號進行諧波小波包變換下各頻帶內的重構信號及頻譜圖。 可以看出,圖4中的110 Hz、圖5中的191 Hz、圖7中的430 Hz、圖9中的700 Hz、圖10中的820 Hz線譜都很清晰地在各個頻段突顯出來。 與諧波小波時頻圖和功率譜圖相比較,由于諧波小波包可以將需要分析的頻帶從整個頻帶范圍內拿出來分析,減少了頻帶之間的相互干擾,使得各窄帶內的分量表示地更清晰,對于淹沒在強噪聲背景下的微弱信號檢測有重要意義。 圖4 0~125 Hz頻段的分析與重構結果 圖5 125~250 Hz頻段的分析與重構結果 圖6 250~375 Hz頻段的分析與重構結果 圖7 375~500 Hz頻段的分析與重構結果 圖8 500~625 Hz頻段的分析與重構結果 圖9 625~750 Hz頻段的分析與重構結果 圖10 750~875 Hz頻段的分析與重構結果 圖11 875~1 000 Hz頻段的分析與重構結果。 在介紹諧波小波變換的基礎上,提出了水聲目標輻射噪聲信號的諧波小波包分析方法,并且利用諧波小波包變換檢測出了藉助功率譜分析和諧波小波變換下不能檢測出的線譜成分。對實驗測量所得實測數據的分析表明,諧波小波包變換能夠有效增強水聲目標噪聲中的微弱線譜成分。 [1] 侯鐵雙.基于小波變換和支持向量機的聲引信信號檢測研究[D]. 西安: 西北工業大學,2010. [2] 侯鐵雙.基于解析小波變換的信號包絡檢測[J].西安郵電學院學報,2011,16(3):18-21. [3] 陳敬軍,孟昭文,陸佶人. 模糊專家系統在線譜檢測中的應用研究[J].船舶工程,2006,26(6):67-70. [4] Newland D E. Harmonic wavelet analysis[J].Proceedings of the Royal Society A, 1993,443:203-225. [5] 李舜銘,許慶余. 微弱振動信號的諧波小波頻域提取[J].西安交通大學學報,2004,38(1):51-55. [6] 婁琳,賈耀增.諧波小波自適應濾波技術研究[J].機械科學與技術,2012,31(9):1486-1489. [7] 李彥彥,華晨輝.諧波小波在旋轉機械故障診斷中的應用[J].遼寧工程技術大學學報:自然科學版,2012,31(1):123-126. [8] 王冬云,張建剛,秦紅義,等. 應用諧波小波包提取轉子故障特征方法[J].哈爾濱工程大學學報,2012,33(7):875-880. [9] 田福慶,羅榮.改進的諧波小波包變換及其在微弱故障特征提取中的應用[J]. 震動與沖擊,2013,32(17):29-34. [責任編輯:王輝] Signal detection based on harmonic wavelet packet transform HOU Tieshuang, LUO Zujun, ZHOU You (School of Automation, Xi’an University of Posts and Telecommunications, Xi’an 710121, China) The weak signal can be submerged in the strong signal or ambient noise because of the inter-band interference when the dyadic wavelet is used to detect the line spectrum. To solve this problem, a harmonic wavelet packet transform is proposed to detect the line spectrum. With box-like spectrum of the harmonic wavelet function and according to the nature of the target-radiated noise, the analysed level and bandwidth can be appropriately chosen; therefore the inter-band interference can be reduced. Results show that the harmonic wavelet packet transform can enhance the weak line spectrum components under the low signal-to-noise ratio. underwater signal processing, signal enhancement, harmonic wavelet packet transform 10.13682/j.issn.2095-6533.2014.05.012 2014-03-11 陜西省教育廳專項科研計劃基金資助項目(2011JK0937) 侯鐵雙(1976-),男,博士,講師,從事信號與信息處理研究。E-mail: htshuang@hotmail.com 羅祖軍(1965-),男,博士,副教授,從事現代控制理論研究。E-mail:lzjpool@xupt.edu.cn TN911.7 A 2095-6533(2014)05-0061-05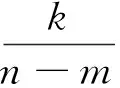



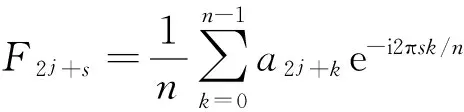

2 諧波小波包變換
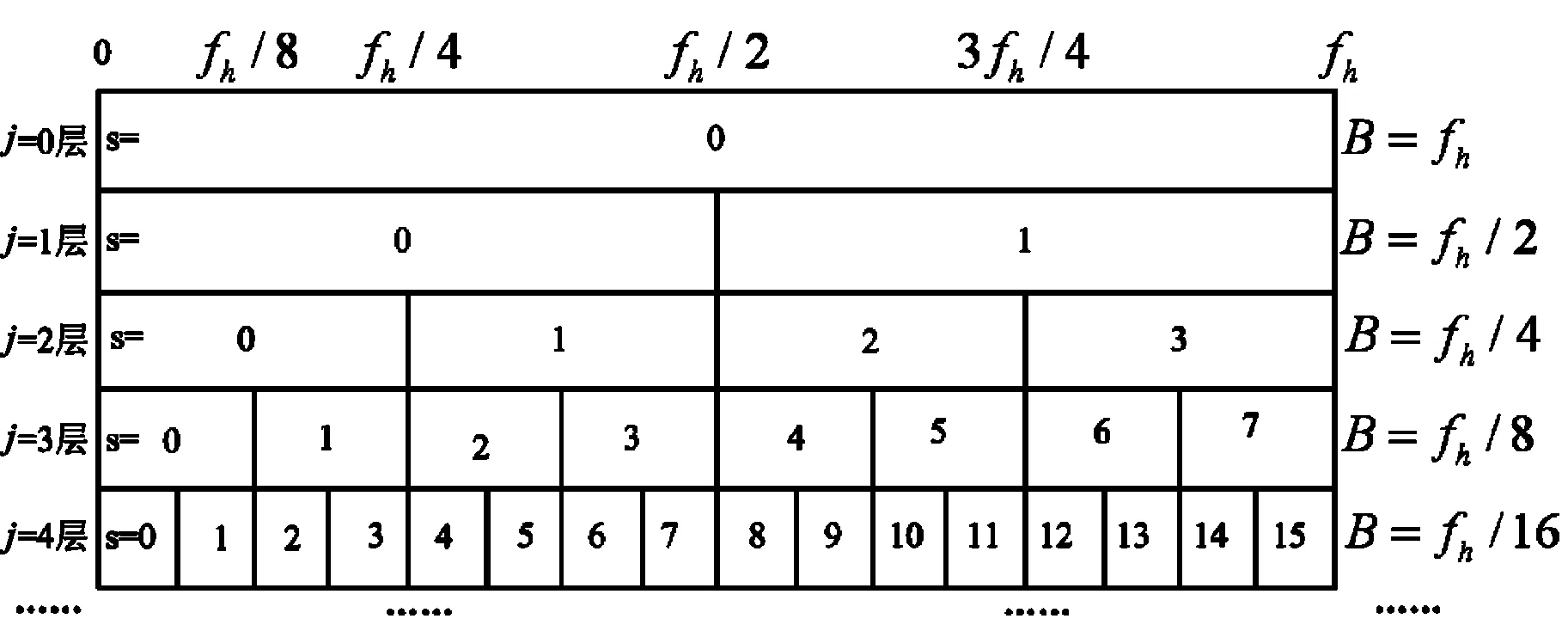
3 諧波小波包分析的數據驗證

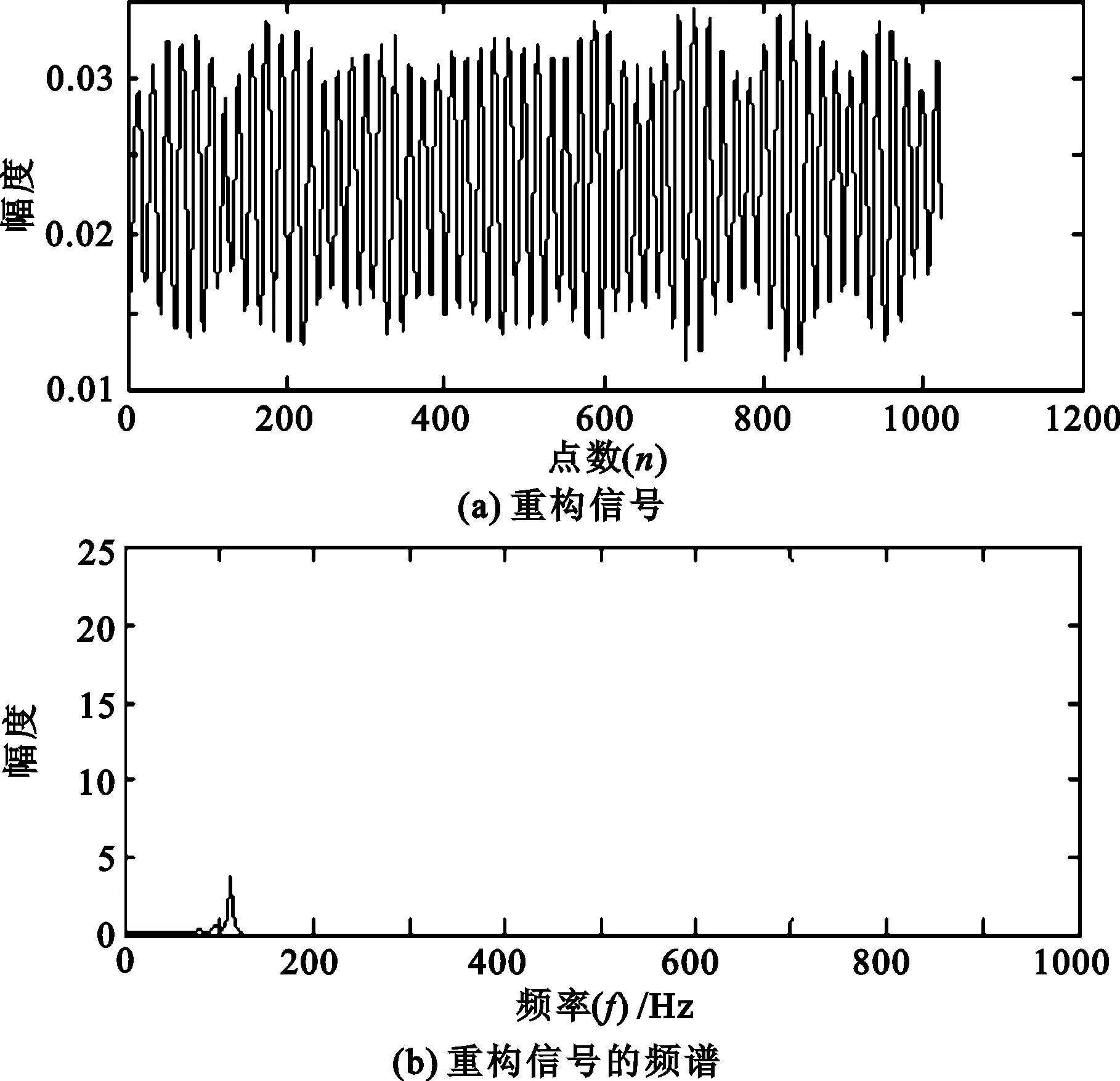





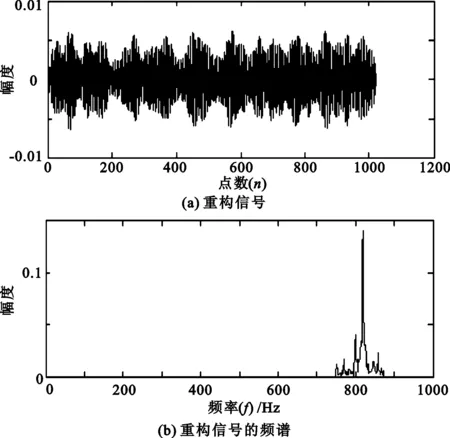
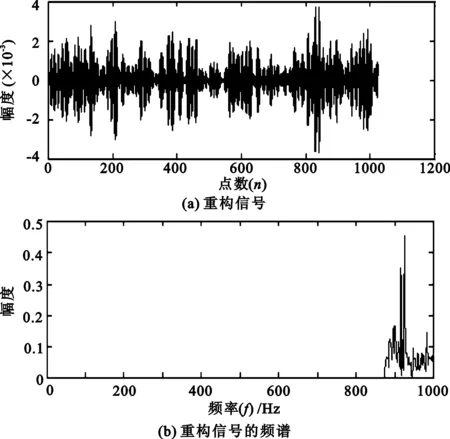
4 結 語

