鐵道車輛液壓減振器聯合仿真模型的構建及其試驗驗證

肖乾，李清華，王成國，張海，，徐紅霞，賈慧芳

(1.華東交通大學載運工具與裝備教育部重點實驗室，江西南昌330013;2.中國鐵道科學研究院鐵道科學技術研究發展中心，北京100081)

液壓減振器是鐵道車輛懸掛系統的重要阻尼元件，它通過節流的方式吸收和緩和道路不平順等引起的振動和沖擊，達到提高車輛安全性、平穩性及舒適性的目的。隨著乘客對列車安全性及舒適性的要求不斷提高，研究減振器性能對車輛動力學性能的影響顯得尤為重要。因此，有必要借助計算機仿真技術建立液壓減振器聯合仿真模型，以期為其嵌入車輛模型研究減振器性能對車輛動力學性能影響建立基礎。

目前，國內外學者對于液壓減振器數學模型的建立方法歸納起來有3種，即參數化建模、等效參數化建模、非參數化建模。參數化建模因考慮了減振器內部油液流動以及節流閥彈性元件的變形等真實工作狀態而應用較多［1］。對于減振器建模大多忽略其兩端的橡膠元件而做了剛性處理，但已經有學者指出減振器節點剛度對其性能及車輛動力學性能有較大影響［2－3］。鑒于上述原因，以下將采用參數化建模的方法以高速列車KONI橫向減振器為例，在Easy5環境下建立液壓減振器液壓控制模型。對建立好的液壓減振器控制模型應用Easy5和ADAMS接口技術在ADAMS環境下建立考慮減振器橡膠節點剛度的Maxwell聯合仿真模型并通過試驗驗證了模型的精確性。

1 減振器參數化建模

1.1 減振器的工作原理

KONI橫向減振器其內部油液是單向流動的，在活塞和底座上都設有單向閥，在活塞桿導向座上設有阻尼調節閥。

如圖1為單向流液壓減振器拉伸和壓縮工作情況。當活塞受到到拉伸力Fe作用時，減振器拉伸長度S，活塞單向閥關閉，活塞上部相當于體積為A的油液從拉伸腔通過阻尼調節閥流入儲油缸，而底座上單向閥開啟相當于體積為 (A+B)的油液通過單向閥流入壓縮腔;當活塞受到壓縮力Fe作用時，減振器壓縮長度S，底座單向閥關閉，活塞單向閥開啟，相當于體積 (A+B)的油液從壓縮腔通過活塞單向閥流入拉伸腔。

圖1 油液單向流動減振器工作原理

1.2 液壓減振器液壓流體力學基礎方程

液壓流體力學是流體力學的一個組成部分，主要研究液體與液壓元件之間的相互作用規律。通過研究液體運動規律和流體運動與力的關系，推導出液體運動的連續性方程、能量方程以及動量方程等流體動力學的基本定律。能量方程加上連續性方程，可以解決壓力、流速或流量及能量損失之間的關系;動量方程可解決流動液體與固體邊界之間的相互作用問題［1，4］。

連續性方程式就是流體流動過程中的質量守恒定律的一種數學表達式，假設流體為不可壓縮，則連續性方程為:

式中:u，v，w分別為x，y，z方向的速度分量。

伯努利方程是流體流動中以其特有的流動參數來反應能量守恒定律的一種表達式:

式中:z1，z2為液面的高度;p1，p2為液面的壓力;v1，v2為液面的流速;hw為能量損耗;ρ為液體密度。

根據流體力學理論知識，當小孔的通流長度l與孔徑d之比l/d≤0.5時稱為薄壁小孔流。通過薄壁小孔的流量可以由下式求得:

式中:Q為流經薄壁小孔的流量;Cd為流量系數，一般取0.62～0.63;A0為孔口截面積;ρ為油液密度;Δp為薄壁小孔兩端壓力差。

當小孔的流通長度l與孔徑d之比l/d＞4時，稱為細長小孔流。孔的流量可以由下式求得:

式中:Q為流經細長小孔的流量;d為細長小孔的直徑;η為液體的動力黏度;l為細長小孔的通流長度;Δp為細長小孔兩端的壓力差。

當小孔的流通長度l與孔徑d之比l/d≤4時，稱為管嘴流動。管嘴流動可以由下式表示:

式中:Q為流經管嘴的流量;Cv為流量系數一般取為0.82;a為孔口截面積;ρ為油液密度;Δp為流經管嘴兩端的壓力差。

當液流空間的高度比和寬度小得多時，就稱為縫隙流動。縫隙流動可以由下式表示:

式中:Q為流經縫隙的流量;b為縫隙的寬度;h為縫隙的高度;η為液體的動力黏度;l為通流長度;Δp為流經縫隙的壓力差。

1.3 減振器液壓動力學模型建立

在減振器動力學模型建立中以KONI減振器結構(圖2)及主要結構參數值 (表1)為建模依據，在Easy5下建立減振器液壓系統模型如圖3。

圖2 KONI橫向減振器結構圖

表1 減振器主要結構參數值

圖3 減振器液壓控制模型

模型中用提升閥元件與較大孔徑節流孔元件串聯與較小節流孔元件并聯來模擬減振器阻尼調節閥。用單向閥元件與節流孔元件串聯來模擬活塞單向閥和底閥。用兩個變量容器元件來分別模擬拉伸腔和壓縮腔。用液壓缸元件來模擬工作缸、活塞和活塞桿。用蓄能器元件來模擬儲油缸。

在不影響計算精度的情況下對模型做了如下假設:

(1)在整個工作過程中，減振器內的油液溫度保持不變;

(2)不計壓力變化引起的系統剛性構件的彈性變形;

(3)忽略工作過程中氣泡產生的影響;

(4)不計油液自重;

(5)忽略活塞與工作缸之間、活塞桿與導向座之間的油液泄漏。

2 減振器聯合仿真模型

鐵道車輛上液壓減振器的兩端都因有橡膠連接結構(圖4)而具有彈性剛度，該彈性剛度會使阻尼力與活塞速度及位移之間產生相位變化而影響減振器特性。因而在實際建模中常把減振器簡化成一個阻尼和彈簧串聯的組合元件，稱為Maxwell模型。所以，以下將考慮減振器兩端剛度建立Maxwell聯合仿真模型。

圖4 減振器兩端橡膠連接結構

2.1 聯合仿真模式的選擇

對于Easy5和ADAMS的聯合仿真模式主要有3種［5］(圖 5):

(1)聯合模式，由Easy5和ADAMS求解器求解各自的模型;

(2)控制系統導入模式，將Easy5所建立的控制與多學科系統導入ADAMS，利用ADAMS求解器積分計算所有的模型;

(3)函數評價模式，將ADAMS所建立的多體機械模型導入Easy5，利用Easy5求解器積分計算所有的模型。

圖5 聯合仿真方式原理圖

目前的學者們的研究都是采用控制導入模式進行仿真計算［6－8］，這主要是由于此種模式可以在控制系統預置參數的情況下研究整個模型的性能，采用ADAMS的參數評價功能進行統一的試驗設計和參數優化。因此，在文中也將采用這種聯合仿真模式進行建模分析。

2.2 聯合模型實現過程

(1)在ADAMS中建立簡化的減振器的機構模型，模型中將兩端橡膠連接件等效為一個剛度為1.715×107N/m彈簧。定義活塞速度和位移為輸出變量，阻尼力為輸入變量，通過ADAMS/Controls模塊將Control Plant輸出，生成adm、cmd文件供Easy5配置接入。

(2)將建立好的減振器液壓控制模型中添加ADAMS接口元件來替換原模型中位移和速度激勵元件，在ADAMS接口元件中添加之前導出的adm、cmd文件從而實現與ADAMS機構模型的連接，然后導出dll文件。

(3)在ADAMS/View中通過Contol模塊導入dll文件建立動態聯合仿真模型，建立的簡化模型如圖6。

圖6 減振器Maxwell聯合模型

3 聯合模型試驗驗證

圖7 減振器外特性仿真曲線

為了驗證減振器聯合模型的準確性，分別在速度0.1 m/s、0.2 m/s、0.3 m/s、 0.4 m/s、0.5 m/s下進行仿真和試驗。仿真結果如圖7，試驗結果如圖8，仿真與試驗結果對比如表2。

圖8 減振器外特性實驗曲線

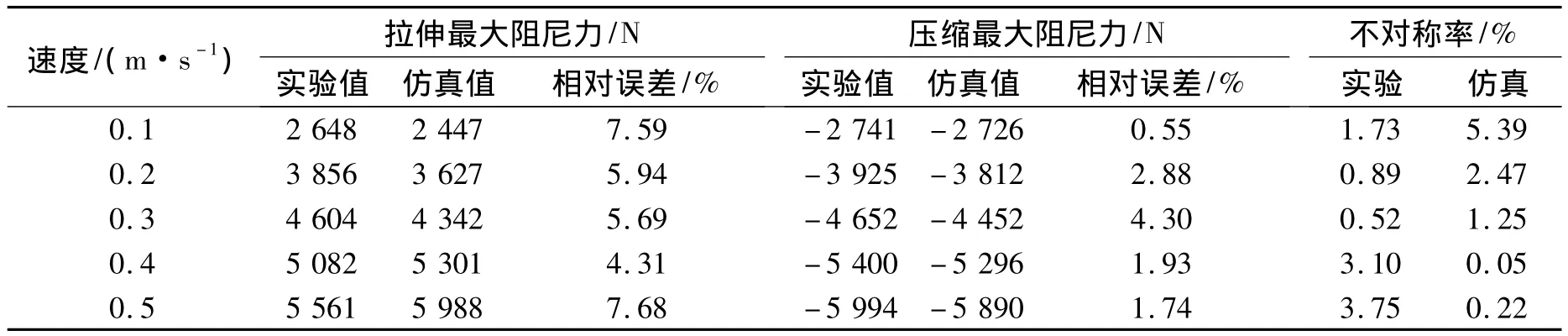
表2 實驗與仿真結果比較

從表2可以看到，仿真拉伸阻尼力最大誤差為7.68%，最小為4.31%;壓縮阻尼力最大誤差為4.3%，最小僅為0.55%。不對稱率最大為5.39%，最小為0.05%，均小于機車車輛油壓減振器技術條件［9］中對稱率要小于10%的規定。由此可以說明所建立的模型較為精確可靠。

4 結論

以鐵道車輛KONI橫向液壓減振器為例，根據其結構和工作原理，在考慮減振器兩端剛度條件下成功建立了鐵道車輛液壓減振器的Maxwell聯合仿真模型。利用建立的聯合模型仿真計算分析了減振器的阻尼特性，并通過對比試驗和仿真結果顯示各項指標誤差均小于10%從而驗證了所建立的減振器聯合模型較為精確。此聯合仿真的建模方法適用于一般機液耦合問題的建模，為后期實現減振器嵌入車輛動力學模型提供了基礎。

［1］孫勝利.位移相關減振器動力學建模及對車輛性能影響的研究［D］.長春:吉林大學，2008.

［2］陸冠東.串聯剛度對液壓減振器特性的影響［J］.鐵道車輛，2007，45(2):1 －5.

［3］曾京，鄔平波.減振器節點剛度對鐵道客車系統臨界速度的影響［J］.中國鐵道科學，2008，29(2):94－98.

［4］徐灝.機械設計手冊［M］.北京:機械工業出版社，1998.

［5］MSC Software Corporation Confidential.基于 Easy5/Adams的高壓開關緩沖器分合閘動力學分析報告［OL］.

［6］李江波，黃明輝，趙興.基于ADAMS與EASY5的大型模鍛液壓機聯合仿真［J］.機械設計與制造，2011(6):235－237.

［7］生龍波，馬吉勝，孫洋河，等.基于ADAMS與EASY5的某履帶車輛制動系統的聯合仿真［J］.機械制造，2012，50(574):28－30.

［8］陳北平，周新建.基于ADAMS與EASY5的雙筒式液壓減振器掃頻研究［J］.機床與液壓，2009，37(12):186 －188.

［9］中國人民共和國鐵道部.TB/T 1491-2004.機車車輛油壓減振器技術條件［S］.中國鐵道出版社，2005.