基于模糊神經網絡滑模控制的xy平臺輪廓控制
王麗梅,左瑩瑩
(沈陽工業大學電氣工程學院,遼寧沈陽110870)
數控加工系統的發展方向是高精密、高速度和高復合化。直接驅動xy平臺已經被廣泛用于高速自動化加工領域[1]。其輪廓精度是單軸跟蹤精度和雙軸聯動精度的合成。為提高輪廓精度,很多方法側重于設計單軸控制器,間接地減小整個系統的輪廓誤差。例如,文獻[2]采用零相位控制抑制了機械延遲對加工系統的影響。文獻[3]采用積分滑模設計了位置控制器,文獻[4]也采用滑模變結構控制進行了位置環和速度環控制器的設計。其共同的缺點是存在抖振問題且控制比較復雜。文獻 [5]闡述了智能控制在直線電機上的應用。隨著智能控制的出現,將現代控制方法與智能控制方法相結合已成為學者們研究的方向。例如,文獻[6]將模糊控制和滑模變結構控制相結合設計了模糊自學習滑模控制器來抑制系統參數變化和外界擾動對系統的影響,其缺點是模糊控制處理信息能力差。文獻 [7-8]采用神經網絡控制和滑模控制相結合對直線電機進行了控制,其缺點是神經網絡控制連接權之間物理意義不清晰且不能完全消除抖振問題,其優點是并行處理信息能力較強。文中將三者結合取其互補性,使模糊神經網絡滑模控制不但連接權之間物理意義清晰,而且具有較強的并行處理信息能力,提高系統魯棒性的同時基本能夠消除滑模變結構控制自身存在的抖振問題。針對直接驅動xy平臺采用此控制方法進行單軸控制器的設計,使單軸具有較好的跟蹤精度,間接地減小輪廓誤差。但是單純提高單軸跟蹤精度不能完全解決輪廓誤差模型復雜對輪廓精度的影響,因此為了直接地減小整個系統的輪廓誤差,進一步提高直接驅動xy平臺對自由軌跡的跟蹤能力,也有學者做了研究[9]。其控制思想是首先建立曲線軌跡的輪廓誤差模型;然后以輪廓誤差作為直接被控量,通過控制器的調節來直接地改善系統輪廓精度。
文中首先采用FNNSMC設計單軸位置協調控制器,用以削弱負載擾動對單軸跟蹤精度的干擾;其次采用實時輪廓誤差估計法對任意軌跡的輪廓誤差進行建模并采用CCC來分配xy兩軸的補償值,使誤差量在有限時間內趨近于零,削弱輪廓誤差模型復雜對系統性能的影響,以滿足PMLSM直接驅動xy平臺的高精度加工要求。
1 直接驅動xy平臺輪廓誤差模型
精確的輪廓誤差模型有利于提高直接驅動xy平臺數控系統的輪廓加工精度,圖1為任意軌跡的實時輪廓誤差模型。其中期望軌跡的加工位置R1(t),實際軌跡的加工位置是P1(t)且期望軌跡上的一點是R'2(t),假設從R'2(t)到R1(t)所需的加工時間為Δt,ex是x軸跟蹤誤差,ey是y軸跟蹤誤差,x軸與直線R1R'2的夾角是φ。

圖1 任意軌跡的實時輪廓誤差
輪廓誤差為P1(t)到直線R1R'2的距離ε,vR1為點R1(t)的平均速度,vP1為點P1(t)的平均速度,v1和v2分別為R1(t)、R'2(t)兩點的切線速度,且下角標x,y分別代表x軸和y軸。由以上這些推出

最終推導出任意軌跡輪廓誤差公式為

2 模糊神經網絡滑模控制器設計
直接驅動xy平臺是由軸向垂直運動的兩臺PMLSM驅動的,由PLMSM工作原理可得其單軸狀態空間方程為
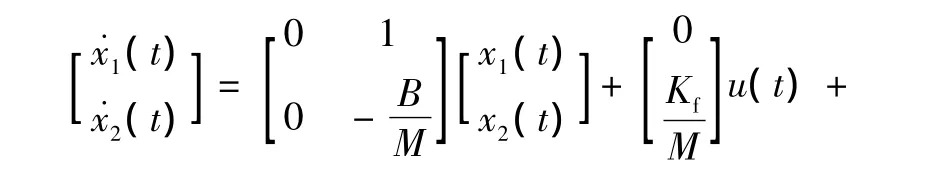

式中:[x1(t)x2(t)]T=[xrvr],Tf為外部擾動且定義跟蹤誤差公式為
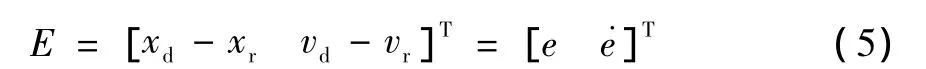
假如速度信號 定義為如下形式

式中:c1>0,c2>0。
定義滑模面切換函數為

當S(t)=0時滿足vr=^vr,并且將式 (8)代入式 (6)和 (7)中,可以得到式 (9)

上式滿足t→∞時e(t)→0,則滑模的等效控制為

式中:UFNN為FNNSMC的輸出,用來代替常規滑模的等效輸出。
文中采用含輸入層、隸屬度函數層、規則層和輸出層的4層模糊神經網絡結構如圖2所示。

圖2 4層模糊神經網絡滑模控制結構圖
定義一個李雅普諾夫函數為v=0.5S2則

式中:滿足當t→∞時S(t)→0,為了使S S·極小化,定義S(t)和S·(t)為所設計控制器的輸入。
第1層:輸入層

第2層:隸屬度函數層
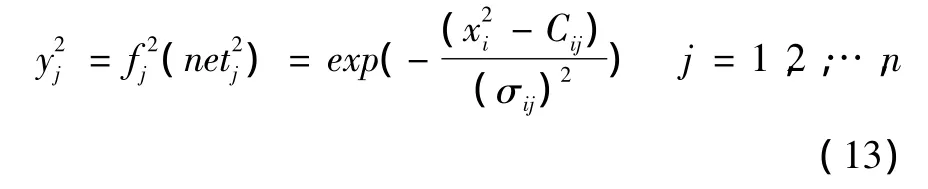
式中:Cij和σij分別為高斯型隸屬函數的均值和標準差。
第3層:規則層


第4層:輸出層

定義目標函數為

通過如下方式來調整輸出層的權值

定義規則層和隸屬度函數層的誤差項為通過如下方式來調整隸屬度函數參數


直接驅動xy平臺系統輪廓控制結構如圖3所示,其中xd,yd和xa,ya表示單軸的輸入輸出,ξx和ξy分別為x、y軸的負載擾動,軸間交叉耦合控制器采用實時性較強的PID控制。

圖3 基于模糊神經網絡滑模控制的xy平臺輪廓控制框圖
3 仿真與分析
文中以心形軌跡為例,采用參數相同的兩臺PMLSM進行仿真,其參數如下:
m=5.8 kg,Kf=10.979 4 N/A,B=244.319 2 Ns/m,交叉耦合控制器的比例、積分、微分增益分別為15,35,5;神經網絡權值w的初值取 [-1,1]之間的隨機值,中心矢量和高斯基寬向量的初始值C=[-3 -1.5 0 1.5 3],σ= [1 1 1 1 1]T。

圖4 指令軌跡與輸出軌跡
圖4為xy平臺的合成輸出曲線。可以明顯地看出:基于模糊神經網絡滑模控制作用下,實際輸出曲線達到了給定的心形軌跡效果。
圖5(a)和 (b)分別為直接驅動xy平臺單軸采用RBF神經滑模控制和模糊神經網絡滑模控制下的輸入響應曲線,可以明顯地看出:在前者控制下,系統存在較大的抖振問題;但是在后者控制下,系統的輸入信號基本不存在抖振問題,因此單軸采用模糊神經網絡滑模控制有效地消除了抖振問題。

圖5 x軸控制輸入
圖6、圖7分別為t=2 s時向各軸突加500 N負載擾動的情況下,單軸采用RBF神經網絡滑模控制和模糊神經網絡滑模控制下的單軸位置誤差曲線。可以明顯看出:位置跟蹤精度均達到了10-4m,但是后者的位置精度明顯高于前者,而且在外界擾動存在的情況下,系統很快地跟蹤上了給定信號,保證了直接驅動xy平臺控制系統具有較好的抗擾性和較強的魯棒性。
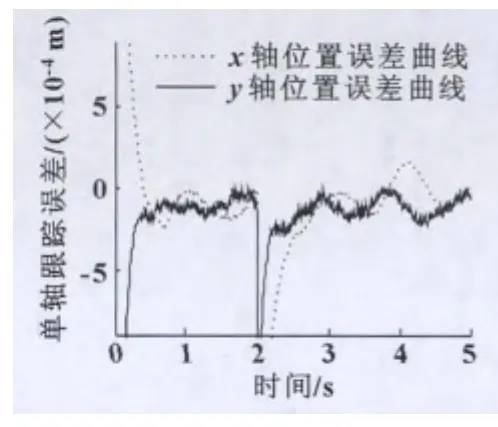
圖6 RBF神經網絡滑模控制+CCC時的位置誤差曲線

圖7 模糊神經網絡滑模控制+CCC時的位置誤差曲線
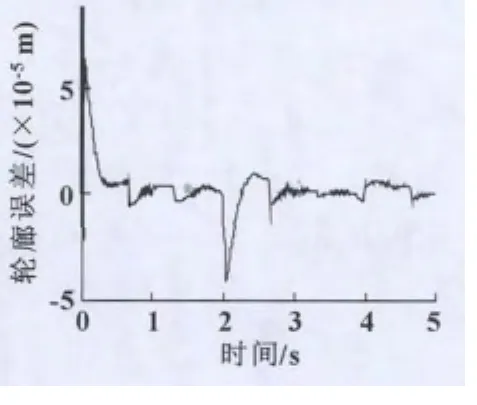
圖8 輪廓誤差曲線
圖8為同樣仿真條件下的直接驅動xy平臺控制系統的輪廓誤差曲線,輪廓精度達到了10-5m,與單軸跟蹤精度相比有了進一步的提高,也就是說交叉耦合控制器的設計有效地減弱了輪廓誤差對系統輪廓精度的影響。
4 結論
針對直接驅動xy平臺加工系統,首先設計了模糊神經網絡滑模位置控制器,削弱抖振的同時抑制了負載擾動對加工系統的影響;其次建立了任意軌跡的輪廓誤差模型且采用傳統的交叉耦合控制設計了軸間協調控制器,有效地削弱了輪廓誤差模型復雜對輪廓精度的影響。仿真結果表明:所設計控制系統有效地提高了直接驅動xy平臺系統的魯棒性和輪廓精度。
[1]趙希梅,郭慶鼎.為提高輪廓加工精度采用 DOB和ZPETC的直線伺服魯棒跟蹤控制[J].電工技術學報,2006,21(6):111 -114.
[2]趙希梅,郭慶鼎.基于ZPETC和CCC的直接驅動XY平臺高精度控制[J].組合機床與自動化加工技術,2011,21(6):111-114.
[3]王麗梅,林淑.雙直線電機數控平臺精密輪廓跟蹤控制補償方法研究[D].沈陽:沈陽工業大學,2012:20-35.
[4]曾岳南,范勵超.永磁同步直線電機滑模控制的研究[D].廣州:廣東工業大學,2012:22 -47.
[5]吳雪芬.基于自適應神經網絡的PMLSM速度控制研究[J].電氣傳動,2008,38(6):37.
[6]孫宜標,郭慶鼎,孫艷娜.基于模糊自學習的交流直線伺服系統滑模變結構控制[J].電工技術學報,2001,16(1):52-56.
[7]李海俠.遺傳神經網絡滑模控制在交流伺服控制中的應用研究[J].機械設計與制造,2012(7):142-145.
[8]王偉,易建強,趙冬斌,等.一種新型神經網絡滑模控制器的設計[J].電機與控制學報,2005,9(6):603 -606.
[9]SUN Dong,SHAO Xiaoyin,FENG Gan.A Model-free Crosscoupled Control for Position Synchronization of Multi-axis Motions[J].IEEE Transactions on Control Systems Technology,2007,15(2):306-314.

