基于單元信息熵的半色調圖像有效子塊提取*

林海龍，文志強，喻魁蘭

基于單元信息熵的半色調圖像有效子塊提取*

林海龍，文志強，喻魁蘭

（湖南工業大學計算機與通信學院，湖南株洲412000）

針對數字半色調圖像有效子塊的提取，提出了圖像的單元熵及熵矩陣構造的算法.首先，將半色調圖像分割成若干子塊，對每一個子塊的每一個像素點計算熵，得出熵矩陣.然后，對熵矩陣取均值及方差.最后，根據信息理論可得，當熵的均值越大且方差越小時，越能有效地獲得子塊.實驗表明，通過單元信息熵獲取的有效子塊，含有信息量大，紋理變化平緩，適合用于分類.

半色調圖像；單元熵；熵矩陣；圖像分割

數字圖像的半色調技術是將一幅連續的灰度圖像通過一定的技術轉換成僅含有黑白兩點的二值圖像，使用黑白兩點的密度來表示灰度圖像的灰度值，利用人眼的低通濾波性使半色調圖像與原始圖像相近.半色調技術廣泛應用于噴墨式打印、激光打印（電子照相）中，近幾年隨著計算工業的發展，半色調市場更廣.具體將其分為誤差分散法（Error Diffusion）、點分散法（Dot Diffusion）、有序抖動法（Ordered Dithering）.

在紙質圖像數字化、數字出版系統與半色調圖像的銳化、較色、壓縮等圖像再處理領域，需要將半色調圖像轉換成連續色調圖像，即圖像的逆半調過程.逆半調技術的研究始于上世紀90年代并取得一定的成果，數字圖像的半色調圖像主要是在原圖中引入噪聲的過程，關于濾去噪聲，文獻［1］提出線性濾波和迭代技術，但通過濾波會降低圖像的質量減少圖像的邊緣信息，所以相繼提出將圖像的邊緣和前景分開的小波逆半調.此外還有專門針對誤差分散核的逆半調技術誤差分散核估計、最大后驗概率估計（MAP）等.針對有序抖動的逆半調方法：中值濾波、邏輯濾波.現有逆半調技術需要知道半色調圖像的類別及參數［2］，或者區分圖像的半調種類［3］，或者只是針對某一種類型［4］，這便使得逆半調技術的有效性、靈活性、自適應性受到限制，所以對半色調圖像類別的區分便顯得特別重要.在半色調圖像的分類中由于涉及圖像數量眾多，若對單一圖像進行特征提取便會影響其效率，并且若一副圖像中某一區域像素值均為0或者均為1，那么該部分為無效區域，所以對半色調圖像有效子塊的提取就十分重要.文獻［5］對半調圖像的特征提取作了相關的研究，但均未對有效子塊提取作相應的討論.文獻［6］通過提出了一種新的基于信息熵的圖像檢索，但由于圖像中相鄰的單元格之間存在一定的相關性，所以構建的熵矩陣亦存在一定的信息冗余.本文將熵矩陣的思想應用于數字半色調圖像有效子塊的提取并作相應的改進，以圖像每個元素為中心，一定步長為半徑計算該區域熵且對邊界作相應處理，將整幅圖像構造成熵矩陣，且對熵矩陣的均值和方差作統計分析，計算出有效子塊提取的閥值.該算法的設計能夠消除文獻［4］熵矩陣的信息冗余.

1 基于圖像信息熵的圖像分割

信息是事物運動狀態或存在方式的不確定性的描述，香農將熵作為該種狀態或方式不確定性的一種量度.這種不確定性在概率論中使用隨機事件來描述，假設存在隨機事件X1，X2，X3，…，Xn，其出現的概率分別滿足P1，P2，P3，…，Pn，且滿足下列條件：

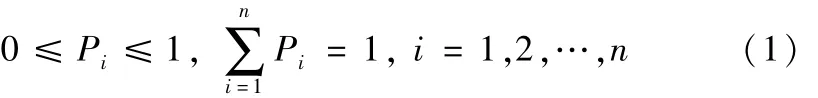
則信息熵的定義為：

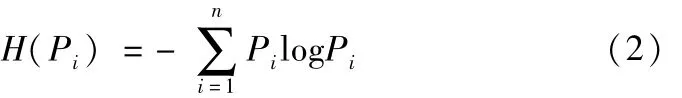
由公式（2）可知，圖像的全局信息熵是一個關于圖像像素值的概率函數，其反映的是一副圖像的全局統計特征，如同圖像的直方圖一樣并未考慮圖像的空間關系，兩幅視覺效果完全不同的圖像其全局信息熵完全可能相等，所以全局信息熵并不能完全顯示圖像的差異性質.圖像的局部信息熵反映了圖像的局部灰度分布的統計特征，相對于圖像的全局信息熵來說，其反映了圖像的空間分布信息.文獻［7－9］中運用網格描述符GD（Gird Descriptor）描述圖像，算法中先將圖像置于固定分辨率的網格上，如圖1所示［6］，圖像占據單元格（超過一定的閥值）則將單元格賦值“1”，反之，賦值“0”.則形成一個含有0、1的二值矩陣，將其從左至右，由上至下順序排列用來描述圖像，顯然在網格的分辨率越高，其識別度就越高.

由于GD網格描述法并未考慮圖像的顏色，僅僅將圖像用0、1來描述，文獻［6］在基于GD的基礎上提出了單元熵.將圖像置于一分辨率固定的網格中（分辨率隨圖像的尺寸變化，定義w、h分別為圖像的尺寸，cw、ch設定為單元格的尺寸，則分辨率為w／cw*h／ch），在每個網格中賦值并非采用GD賦值法，而是計算每個網格的信息熵，假設單元為（i，j），E（i，j）為單元熵，定義

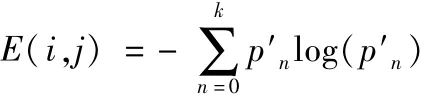
從而形成一個w／cw*h／ch的信息熵矩陣.

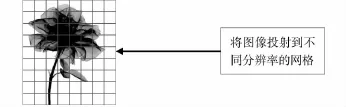
圖1 圖像的網格描述

2 基于單元熵的半色調圖像有效子塊提取

本小節的主要任務是提取半色調圖像的有效子塊，參考眾多文獻發現，相關理論并不多.孔月萍等人在文獻［5］中提到一維自相關函數和灰度梯度共生矩陣分類算法只是將整幅圖像進行特征提取，用提取出來的特征進行分類，很顯然這種方法會大大降低其效率.

孫君頂等［6］指出由單元熵構成的熵矩陣在表達圖像的局部特征上，優于圖像的全局信息熵且單元熵體現了圖像的顏色特征.但是由于原圖相鄰單元格之間存在一定的相關性，所以在熵矩陣中，相鄰的熵具有一定的信息冗余.本小節對單元熵的計算進行改進形成新的熵矩陣消除相鄰熵之間的信息冗余，之后根據信息熵理論選出一幅二值圖像的有效子塊.

假設存在圖像f（x，y）（0＜x＜w，0＜y＜h），分割成fi（xi，yi）子塊，其中（0＜xi＜k，0＜yi＜k）、（0＜i＜w／k*h／k），算法設計如下：

（2）將圖像的子塊fi（xi，yi）劃分為以下區域：區域Ⅰ（0＜xi＜k－m／2，0＜yi＜m／2），區域Ⅱ（0＜xi＜m／2，m／2＜yi＜k－m／2），區域Ⅲ（0＜xi＜k－m／2，k－m／2＜yi＜m），區域Ⅳ（k－m／2＜xi＜k，0＜yi＜k－m／2），區域Ⅴ（k－m／2＜xi＜k，k－m／2＜yi＜k），剩余部分為區域Ⅵ.對于子塊中的每一個像素劃分出分塊fij（xij，yij），其中（0＜j＜k）、（0＜xij＜m，0＜yij＜m）.

（3）根據信息熵公式計算出分塊fij（xij，yij）的熵，并且求得fi（xi，yi）熵矩陣Qi.

3 實驗結果及分析

本實驗在Windows XP操作系統環境下進行操作，采用VC6.0結合OpenCv及matlab進行編程.從十二類半色調圖像庫中，隨機選出409幅圖片，改變半色調圖像子塊的k值大小，計算出每個子塊每個像素點的單元熵形成熵矩陣，實驗證明通過該算法獲取的有效子塊信息含量大且紋理變化平緩，適合分類.

為了能夠給出一個關于μ、σ的范圍，更準確地找出半色調圖像的有效子塊，筆者計算出十二種半色調圖像子塊的μ、σ值（均為（w／k）*（h／k）*409*12個），對其進行統計，結果如圖2.

從特征圖上可以看出隨著k值的增大，μ和σ趨于0的比例會越來越小，也就是圖像的信息越來越豐富，但信息之間的差異會越來越大.為了權衡μ和σ值，使其在分類中取得最佳值，筆者設定一個比例L，μα值為局部信息熵均值μ從大到小值，σβ值為σ為局部信息熵方差從小到大值.那么得出μα、σβ分別為比例L的函數，表示為：μα＝f（L）、σβ＝Ψ（L）.當L分別取初值為10%步值為10%時的μα、σβ的統計值如表1所示.

表1的μα值和σβ值體現在二維坐標圖上，如圖3所示.

由圖3可以看出μα是一個隨L增加遞減的值，σβ是一個隨L增加遞增的值，二者交于一點.根據有效子塊的判別依據：局部信息熵μα越大、σβ值越小，越適合分類，可以得出在相交點的右邊區域為無效區域（不會選擇一個μα值越來越小、σβ值越來越大的子塊作為分類子塊）.其值的大小與比例L有關，根據所需要分類圖像以及圖庫的數目的多少選取L值，由表1和圖3可以得出μα、σβ值，L取值越小，那么μα值就會越大，σβ值就會越小，子塊就越適合分類.取k＝64，L＝10%，μthresh＝0.5903，σthresh＝0.2801作為有效子塊的閥值，當μ≥μthresh，σ≤σthresh時，圖像適合分類.

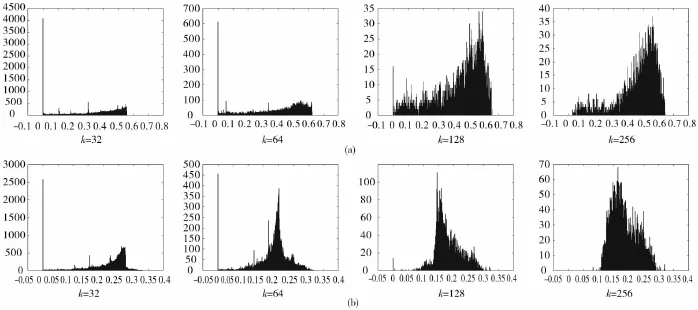
圖2 參數μ、σ的特征圖.（a）參數μ的特征圖；（b）參數σ的特征圖

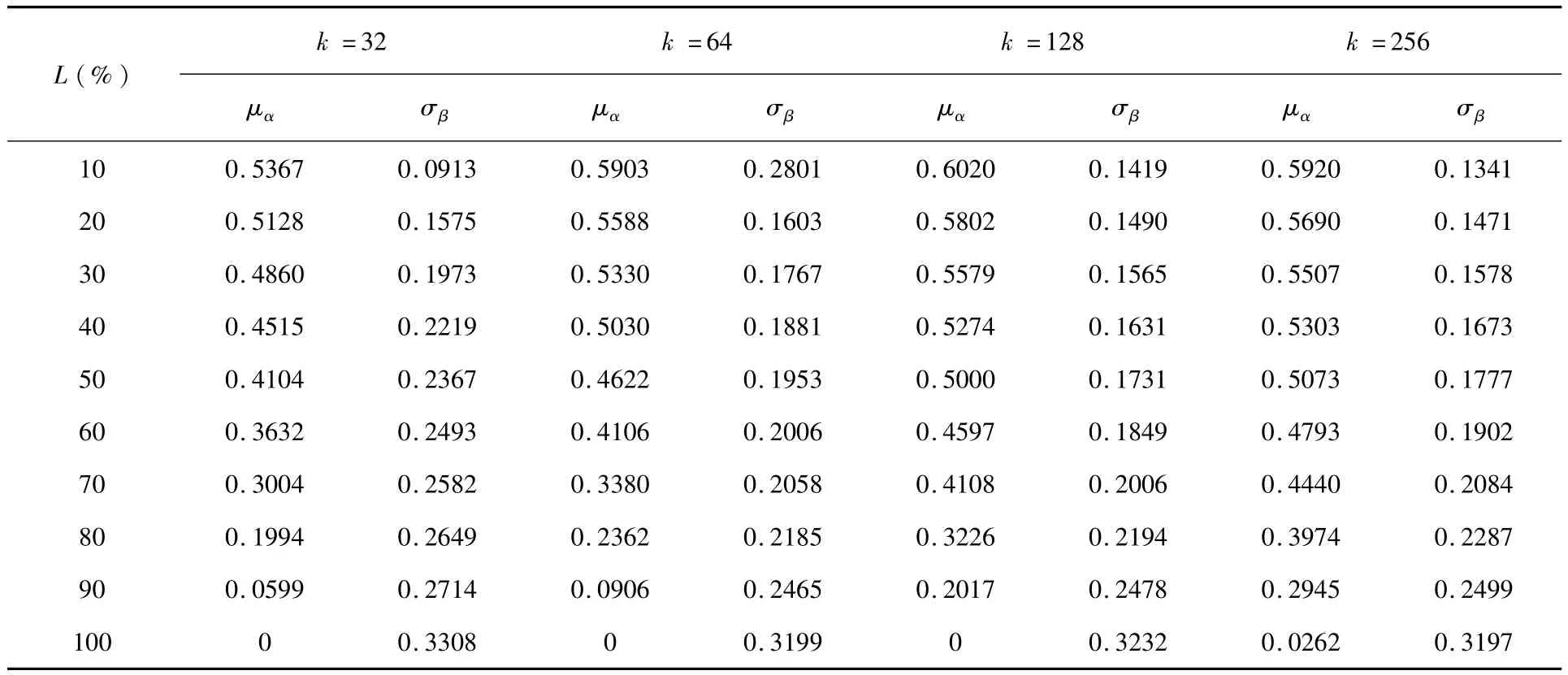
表1 L及μα、σβ統計表

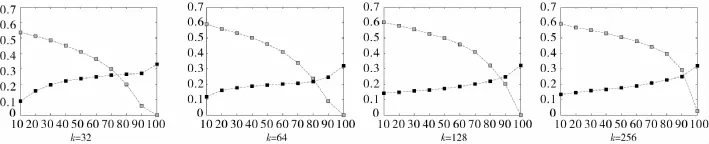
圖3 L及μα、σβ分布圖

4 小結

本文以半色調和逆半調技術為背景，通過研究發現在圖像重建過程中需要知道半色調圖像產生的方法，因此半色調圖像分類十分重要.當前未曾報道過半色調圖像有效子塊的提取，而一幅用于分類的圖像并非所有區域均是有效適合分類的，若對整幅圖像進行特征提取，那么會大大降低效率.本文在基于單元熵的基礎上構造出熵矩陣并對熵矩陣進行均值、方差的統計分析，得出了無效區域和最佳有效子塊閥值.

［1］Kern R S，Stockham Jr TG，Strong D C.Descreening via linear filtering and iterative techniques［A］.Proc SPIE 1913，Human Vision，Visual Processing，Digital Display IV［C］.San Jose，1993.

［2］Wong PW.Inverse halftoning and kernel estimation for error diffusion［J］.Image Processing，IEEE Transactions on，1995，（4）：486－498.

［3］Mese M，Vaidyanathan P P.Look－up table（LUT）method for inverse halftoning［J］.Image Processing，IEEE Transactions on，2001，（10）：1566－1578.

［4］Stevenson R L.Inverse halftoning via MAP estimation［J］.Image Processing，IEEE Transactions on，1997，（4）：574－583.

［5］孔月萍，杜旭苗.一種半調圖像類型識別方法［J］.計算機應用研究，2009，（12）：4850－4851.

［6］孫君頂，毋小省.基于信息熵的圖像檢索［J］.西安電子科技大學學報（自然科學報），2004，（2）：224－228.

［7］Lu G，Sajjanhar A.Region－based shape representation and similaritymeasure suitable for content－based image retrieval［J］.Multimedia Systems，1999，（2）：165－174.

［8］Safar M，Shahabi C，Sun X.Image retrieval by shape：A comparative study［A］.Proceedings of ICME 2000［C］.New York：IEEE，2000.

［9］Chakrabarti K，Ortega－Binderberger M，Porkaew K，etal.Similar shape retrieval in MARS［A］.Proceedings of ICME 2000［C］.New York：IEEE，2000.

Extraction of Effective Sub－blocks of Halftone Images Based on Unit Entropy

LIN Hailong，WEN Zhiqiang，YU Kuilan
（School of Computer＆Communication，Hunan University of Technology，Zhuzhou Hunan 412000，China）

In allusion to the extraction of effective sub－blocks of digital halftone images，this article proposes the unit entropy of images and the algorithm for the entropymatrix construction.Firstly，the halftone image is divided into several sub－blocks，and then the entropy for each pixel pointof each sub－block is calculated to obtain the entropymatrix.Secondly，the study calculates themean and variance of entropymatrix.Lastly，according to the information theory，when the entropy of themean is greater and variance is smaller，sub－blocks can bemore effectively obtained.Experimental results show that effective sub－blocks acquired through the unit entropy contain a large amount of information and the texture changes smoothly，so they are suitable for the classification.

halftone image；unit entropy；entropymatrix；image segmentation

TP391

A

1008－4681（2014）02－0028－04

（責任編校：晴川）

2013－12－18

國家自然科學基金（批準號：61170102）資助項目；湖南省自然科學基金（批準號：11JJ3070）資助項目；湖南省教育廳科研項目（批準號：12A039）.

林海龍（1986－），男，江西上饒人，湖南工業大學計算機與通信學院碩士生.研究方向：圖像處理.