無軸承永磁同步電動機徑向力模型
李可,孫曉東,楊澤斌
(江蘇大學 a.電氣信息工程學院;b.汽車工程研究院,江蘇 鎮江 212013)
無軸承永磁同步電動機(bearingless permanent magnet synchronous motor,BPMSM)具有體積小、重量輕、效率高、功率因數高、控制特性好等優點,還具有磁軸承無摩擦、無磨損、不需潤滑、高轉速和高精度等優點,因此在航空航天、生物醫藥、半導體制造等特殊領域具有廣泛的應用前景[1-5]。
為了保證BPMSM的穩定懸浮運行,必須對徑向力進行實時控制,因此徑向力的精確計算是電動機本體設計和控制策略研究的基礎。文獻[6]對表貼式BPMSM的數學模型進行試驗研究,在得到電感系數的前提下,采用虛位移原理確定了BPMSM徑向力模型,該方法必須依賴試驗數據,因此計算較為復雜,影響徑向力模型的準確性。文獻[7-8]分別對插入式、埋入式BPMSM的數學模型進行了深入研究,首先得到轉矩和懸浮兩套繞組交鏈的磁鏈方程,在此基礎上求得電磁能方程,再根據虛功原理求得徑向力方程。文獻[6-8]對BPMSM的徑向力模型進行研究時并沒有對轉子偏心情況下的徑向力進行深入分析研究,是一種比較理想的徑向力方程,但在實際運行過程中,BPMSM定轉子之間的偏心是存在的。針對現有模型的不足,結合麥克斯韋張量法及磁路法,建立考慮偏心位移的BPMSM徑向力模型,并運用有限元分析對其進行仿真。
1 BPMSM徑向力產生原理
BPMSM定子中疊繞著轉矩繞組和懸浮力繞組,由于懸浮力繞組產生的磁場打破了原有轉矩繞組(包括永磁體,下同)建立的氣隙磁場的平衡,從而產生作用在轉子側的徑向力。設BPMSM的懸浮力繞組和轉矩繞組的極對數分別為PB和PM(下標B,M分別表示懸浮力繞組和轉矩繞組的相關參數),BPMSM要同時實現穩定旋轉和懸浮運行,必須滿足3個條件:(1)兩套繞組的極對數相差1,即PB=PM±1;(2)兩套繞組產生的旋轉磁場方向相同;(3)通入兩套繞組中的電流頻率相同[9]。
BPMSM的徑向力產生原理如圖1所示。圖中,PM=1且PB=2;NBa和NBb為懸浮力繞組,NMa和NMb為轉矩繞組,兩者疊壓在BPMSM的定子槽中。懸浮力繞組通電后產生四極氣隙磁通Ψ4,原本由永磁體產生的二極磁通Ψ2的平衡被四極氣隙磁通Ψ4打破,由于氣隙磁通的不均勻分布進而產生徑向力。如果BPMSM轉子位于中心位置,二極氣隙磁通Ψ2主要由BPMSM轉子表面的永磁體產生,當BPMSM空載懸浮運轉,對應的轉矩繞組中的電流很小,由轉矩繞組電流產生的磁通可以忽略不計。如果NBa和NBb中不通入電流,二極磁通Ψ2保持平衡,此時徑向力為0。當繞組NBa中通正向電流,產生的四極氣隙磁通Ψ4使轉子右側氣隙1處磁通密度增加,轉子左側氣隙3處磁通密度減小,從而產生沿x軸正方向的徑向力;當繞組NBa中通反向電流,則會產生沿x軸負方向的徑向力。同理,沿y軸方向的徑向力可以通過在繞組NBb中通入電流獲得。因此,通過控制懸浮力繞組NBa和NBb中的電流就可以控制懸浮力的大小和方向,從而實現轉子的穩定懸浮。
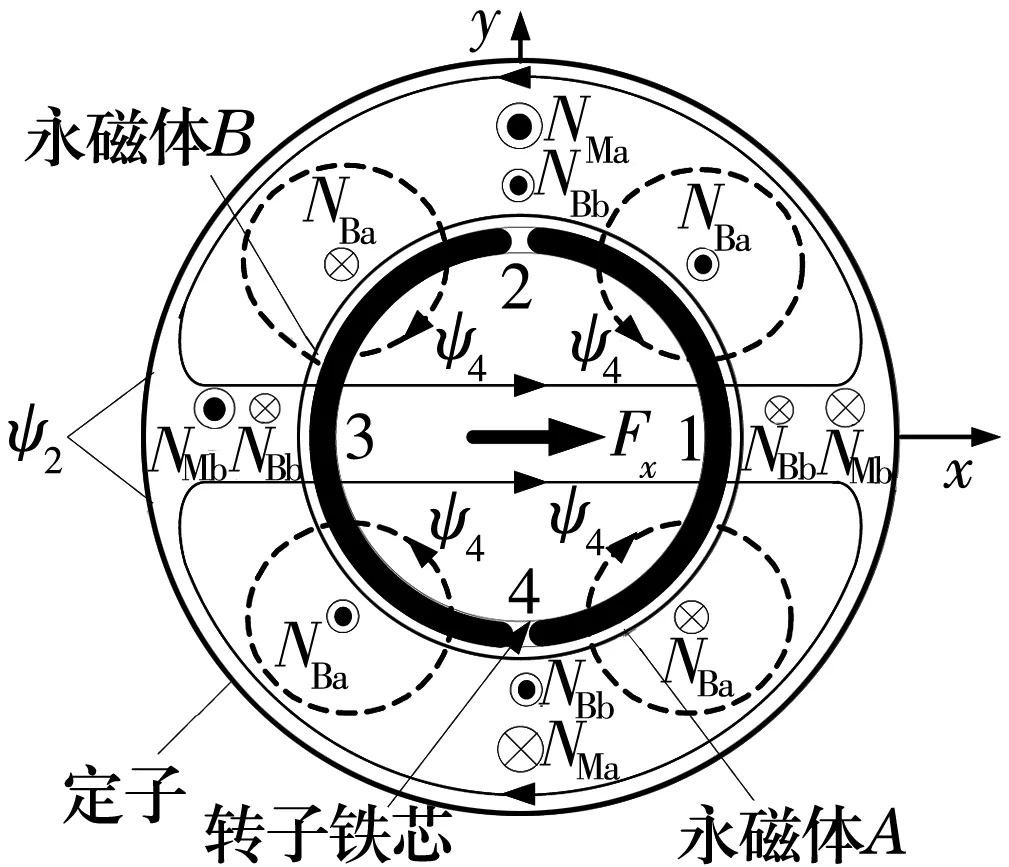
圖1 徑向力產生原理
2 徑向力模型
根據麥克斯韋張量法,BPMSM轉子表面dS面積上沿機械角θ受到的法向力和切向力分別為[10]
(1)
bt(θ,t)=-Btcos(ωt-PMθ-γM),
(2)
式中:bn(θ,t)和bt(θ,t)分別為轉矩繞組和懸浮力繞組的合成氣隙磁密的法向和切向分量;θ為沿定子內表面逆時針機械角度;μ0為真空磁導率;Bt為切向氣隙磁密幅值;γM為PM對極氣隙磁動勢基波的空間初始相位角;ω為電角頻率。
由(1)式可得徑向力在α和β方向上的分量為
,(3)
式中:r為轉子外半徑;l為轉子鐵芯有效長度。
BPMSM定、轉子之間偏心位移如圖2所示。圖中,O′(α,β)為偏心轉子軸心的坐標;g0為BPMSM定、轉子之間的平均氣隙長度;R為定子的內半徑。定、轉子之間的氣隙長度g(θ)為
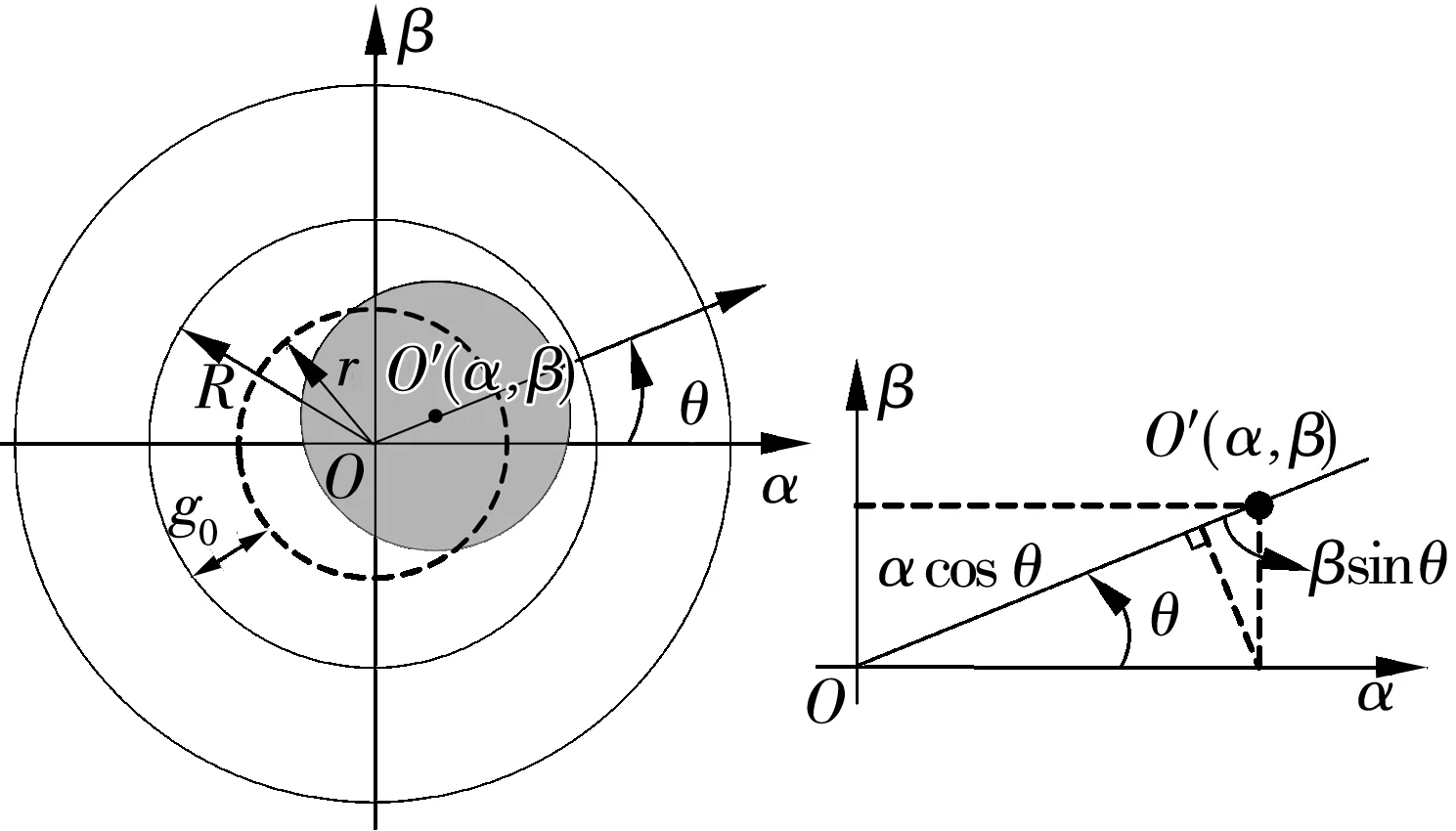
圖2 轉子偏心位移
g(θ)=g0-g1=g0-(αcosθ+βsinθ),
(4)
式中:g1為定、轉子之間的偏心氣隙長度;α和β分別為轉子沿α和β方向的徑向位移。
由于BPMSM在穩定懸浮工況下運轉,定、轉子之間的偏心氣隙長度g1與平均氣隙長度g0相比較小,因此可以忽略,則氣隙長度倒數為
(5)
單位面積內的氣隙磁導分布函數為
(6)
由BPMSM中PM對極轉矩繞組電流與轉子永磁體磁場共同建立的合成氣隙磁動勢的基波分量,以及PB對極懸浮力繞組建立的氣隙磁動勢的基波分量分別為
(7)
式中:FM,FB分別為PM對極和PB對極氣隙磁動勢基波幅值;γB為PB對極氣隙磁動勢基波的空間初始相位角。由兩套繞組共同產生的氣隙磁通密度分別為
(8)
從而可得BPMSM氣隙磁密的法向分量為
bn(θ,t)=bM(θ,t)+bB(θ,t) 。
(9)
假設均勻氣隙下PM對極和PB對極氣隙磁通密度幅值分別為
(10)
式中:NM,NB分別為轉矩繞組和懸浮力繞組每相串聯有效匝數;IM,IB分別為轉矩繞組勵磁電流(包括轉子永磁體激勵的磁場等效至轉矩繞組中的電流部分)和懸浮力繞組電流幅值。
將(2)式和(8)式代入(3)式進行積分,可得α,β方向上轉子受到的徑向力。考慮到徑向位移α和β,以及氣隙磁通密度幅值BM的數值較小,故忽略其平方項,可得
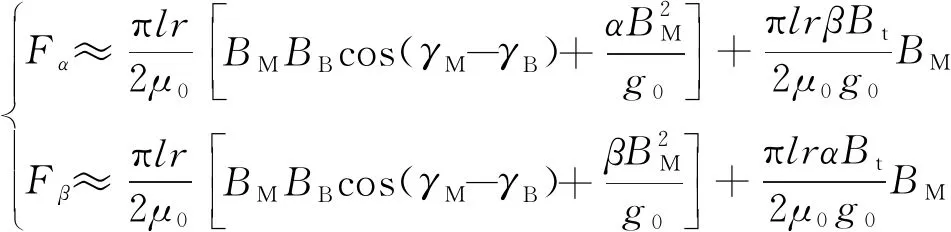
。(11)
轉矩繞組每相氣隙磁鏈值為
(12)
又有
ψM=LMIM,
(13)
式中:ΦM為每相氣隙磁通值;LM為轉矩繞組互感。則(11)式可以化簡為
(14)
由(14)式可知,BPMSM的徑向力由3部分組成:(1)不計偏心時,由轉矩繞組氣隙磁場與懸浮力繞組電流相互作用產生的可控徑向力(徑向力的主要組成部分);(2)定、轉子偏心引起的單邊磁拉力;(3)由于氣隙磁密沿氣隙圓周在轉子表面切向分布不均而產生的徑向力。
3 仿真與分析
為了驗證所建徑向力模型的正確性和有效性,采用有限元方法進行仿真分析。有限元分析參數采用試驗樣機參數:定子外徑140 mm,定子內徑77 mm,轉子外徑75 mm,永磁鐵厚度2 mm,定子槽數24,氣隙1 mm,鐵芯長度100 mm,懸浮力繞組匝數80,轉矩繞組匝數80,永磁鐵剩余磁感應強度1.2 T,矯頑力900 kA/m,轉矩繞組極對數2,功率2 kW,電動機氣隙2 mm,36槽,電動機轉矩繞組電阻3.24 Ω,直軸和交軸電感0.012 H,轉動慣量0.015 8 kg·m2,懸浮力繞組極對數3,懸浮力繞組電阻2.32 Ω,輔助機械軸承氣隙0.5 mm。
轉矩繞組電流為額定值3 A,懸浮力繞組電流分別為1,3和5 A,且定、轉子在x軸方向偏心位移為α時,徑向力與懸浮力繞組電流的關系如圖3所示。
由圖3可知,徑向力的理論計算值直線的斜率均相同,即當定、轉子偏心的變化量相同時,徑向力的變化量也相同,說明當轉矩繞組和懸浮力繞組中通入的電流大小一定時,由于機械軸承氣隙(最大可偏距離)遠小于電動機氣隙,徑向力與定、轉子偏心之間的非線性關系不明顯,可近似為線性關系。當定、轉子在x軸方向偏心時,x方向徑向力的變化要比y方向徑向力的變化顯著,說明x方向的偏心主要影響x方向的徑向力。當電流較小(磁路未嚴重飽和)時,徑向力的有限元計算值與理論值非常吻合,隨著磁路達到飽和,徑向力的有限元計算值雖然開始偏離理論值,但是兩者基本吻合,說明考慮定、轉子偏心位移的徑向力模型能夠較為準確地描述BPMSM的徑向力。
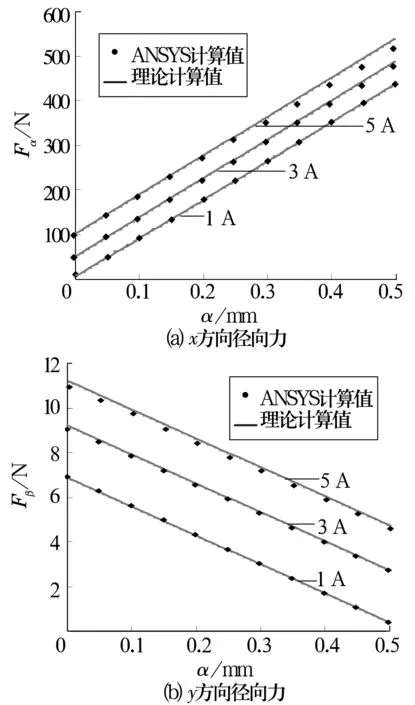
圖3 x方向偏心時徑向力與懸浮力繞組電流關系
4 結束語
在對BPMSM徑向力進行深入分析的基礎上,運用麥克斯韋張量法和磁路法,建立了一種較為精確的BPMSM徑向力數學模型。該模型充分考慮了定、轉子偏心位移,為BPMSM懸浮運行控制的研究和電動機本體設計提供了可靠的理論依據。利用有限元分析方法驗證了該模型的計算精度,為進一步深入研究BPMSM高精度的控制系統打下了基礎。

