圓錐滾子軸承擋邊接觸點的控制方法

沈丹富，孫明亞

(錢潮軸承有限公司，杭州 311215)

符號說明

di——直擋邊內圈滾道最大直徑

Dw——滾子大頭直徑

SR——滾子球基面曲率半徑

β——內圈滾道素線與軸線之間的夾角

λ——內圈大擋邊錐面與端面之間的夾角

ρρ——內圈弧形擋邊曲率半徑

φ——滾子半錐角

Ψ——內圈大擋邊錐面與滾道面之間的夾角

圓錐滾子軸承中,滾子球基面與內圈大擋邊接觸點的位置非常重要，接觸點離內圈大擋邊越程槽過近，工作時越程槽邊緣會處于接觸橢圓區域內而產生應力集中，引起疲勞剝落；接觸點離大擋邊最高點過近，工作中易導致內圈大擋邊變形甚至斷裂。因此，必須對滾子球基面與內圈大擋邊接觸點進行合理控制。文獻[1]從設計角度給出了圓錐滾子軸承滾子球基面與內圈大擋邊的接觸點至越程槽邊緣的距離bi的計算公式，但對于接觸點位置應處于什么尺寸范圍，加工生產過程中應如何有效控制等均沒有相關文獻介紹。為此，現介紹接觸點位置的合理尺寸范圍及其在生產過程中的控制與調整。

1 接觸點范圍的探討

如圖1所示，以圓錐滾子軸承內圈大擋邊與內圈滾道交點為起點，向外依次分為3段，分別標注為0，1/3，1/2，1。根據多年軸承設計以及國外主機配套項目實踐經驗，當接觸點處于0～1/3并靠近根部時，有利于滾子與擋邊形成潤滑楔，且能減小軸承擋邊壓力，但油槽里的油不利于潤滑，接觸點易落入油槽或油槽邊緣，滾子工作時形成邊緣效應，加重滾子球基面磨損，降低軸承壽命；當接觸點處于1/3處時，雖然有利于滾子與擋邊形成潤滑楔，大擋邊壓力強度也較低，但易造成滾子卡死；當接觸點在大擋邊中間1/2處，形成的潤滑楔更有利于軸承潤滑；當接觸點處于大擋邊最高點1處，由于大擋邊壓力強度大，易發生變形。因此，設計上應盡量將接觸點控制在大擋邊中間1/2前后的范圍內。

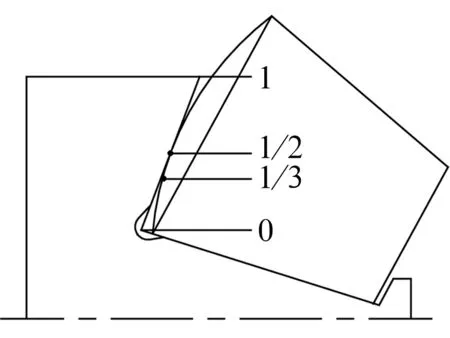
圖1 滾子球基面與內圈大擋邊接觸點位置示意圖

2 接觸點位置的精確計算

根據圓錐滾子軸承純滾動設計理論，軸承內、外滾道素線及滾子中心線交于同一點，滾子與內圈的幾何關系如圖2所示。

由圖2幾何關系得

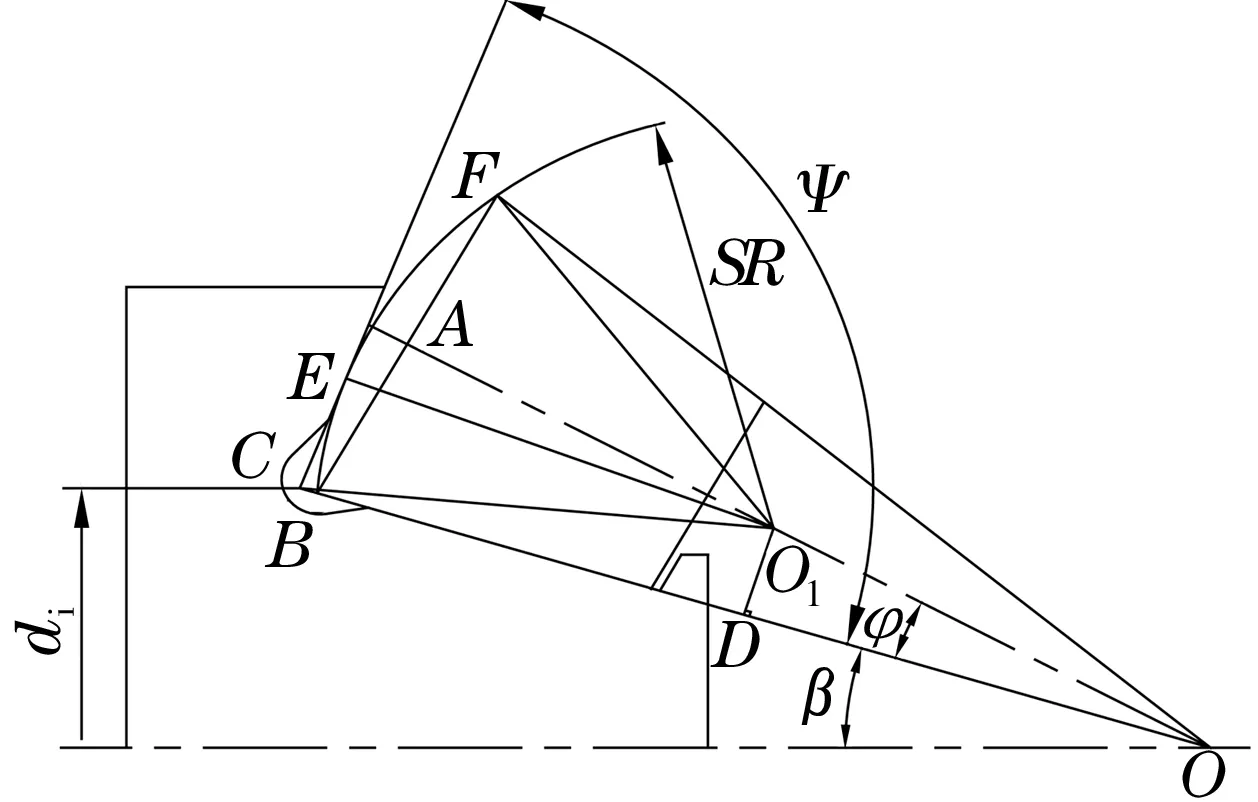
圖2 滾子與內圈幾何關系示意圖

(1)

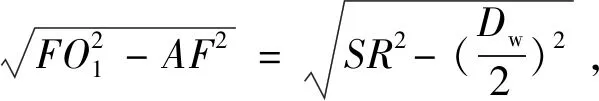
(2)

OO1=AO-AO1，

(3)

O1D=OO1·sinφ，

(4)

(5)

(6)

在RT△O1EC中，接觸點E的精確計算結果為

(7)

則由(1)～ (7)式得，

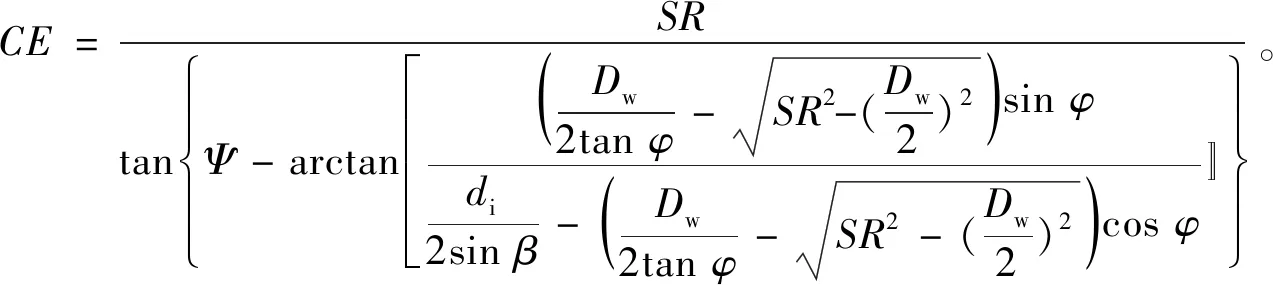
(8)

從(8)式可以看出，在實際生產過程中，只需精確測量出SR，Dw，φ，Ψ，β，di值，并將其代入(8)式，就能精確得到被測軸承接觸點所在位置。由于同一套圓錐滾子軸承中滾子數量較多，滾子球基面精磨過程中難以精確定位，SR值很難精確控制，SR尺寸精度一般在0～15 mm的公差范圍內變動。因此對于SR值，通常需精測多粒(正常情況下精測5粒)滾子，取其平均值作為接觸點精確計算的輸入。

3 接觸點位置的近似計算

如圖2所示，由于CO≈BO，如果CO1≈BO1=SR=0.95ρρ=0.95BO，則CD≈BD，∠O1CD≈∠O1BD，從而有

CD≈BD=BO-DO=BO-O1O·cosφ，

(9)

(10)

(11)

則由(7)式得

(12)

由(1)～(4)式和(9)～(12)式得

(13)

從(13)式可以看出，只需精測SR，Dw，φ，Ψ及5粒滾子SR平均值，可以近似計算出接觸點的位置，不需再對β，di進行精測。

4 生產過程中接觸點位置的控制

無論是新產品試制，還是產品批量生產，都是采用同步工程組織生產，生產周期一般控制在45天內。滾子由專業制造商按圖紙要求及相關技術協議開展生產，需要35天左右完成加工、檢測、包裝；而軸承套圈加工過程相對復雜，一般由專業的鍛造、車加工協作加工，再轉入公司內部檢驗、熱處理、磨加工、裝配，因此需要的時間相對較長。通常情況下，滾子、保持架檢驗合格入庫時，軸承內圈基本進入滾道、擋邊精磨工序，因此，要精確控制接觸點位置，依靠調整滾子幾何參數幾乎是行不通的，只能選擇內圈參數作適當調整。

然而，內圈幾何參數中，β，di是不能變動的，否則不符合軸承純滾動理論，易導致軸承工作過程中滑動摩擦增大，并且會影響軸承裝配后高度。因此，唯一能夠調整的只有Ψ。根據現行圓錐滾子軸承設計方法[2]，Ψ=90°-λ+β，因為β不能變化，因此，改變Ψ實質就是微調λ，即通過微調λ實現接觸點位置的精確控制。

為了更直觀、方便地表達接觸點位置，協助生產、工藝人員準確判斷接觸點控制的是否合理，內圈精磨擋邊前隨機取1～2個內圈，采用軸承檢查儀、輪廓儀精測出圖3所示內圈參數β，di，B，N，F，Ψ及滾子參數SR，Dw，φ，并將接觸點相關計算公式列入Excel表格，借助于Excel表格的功能確定Ψ角的范圍，指導擋邊精磨工序砂輪安裝及角度的調整與控制，達到有效控制接觸點的目的。

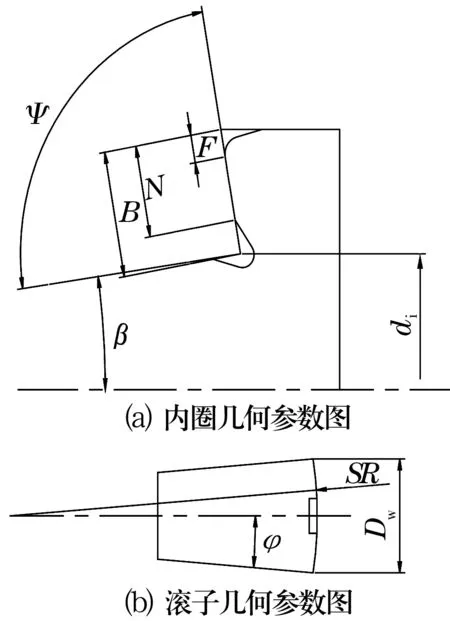
圖3 內圈、滾子需測量的幾何參數

5 接觸點控制實例

以524467圓錐滾子軸承內圈大擋邊與滾子球基面接觸點的實際控制為例，介紹生產過程Ψ的確定及精磨擋邊工序砂輪的調整。

5.1 接觸點位置的計算

接觸點位置的計算步驟為：

(1)利用軸承專用檢查儀、輪廓儀，精確測量滾子、內圈相關幾何尺寸，見表1；

(2)分別將接觸點位置的精確及近似計算公式錄入并設計成2份Excel表格；

(3)根據接觸點位置精確及近似計算式的數據輸入要求，將表1中的測量參數值輸入，得到接觸點的精確、近似計算位置尺寸分別為2.90， 2.89 mm。這2種方法的計算結果僅相差0.01，非常接近，且2種計算結果均顯示接觸點在靠近內圈大擋邊1/2偏上部位。

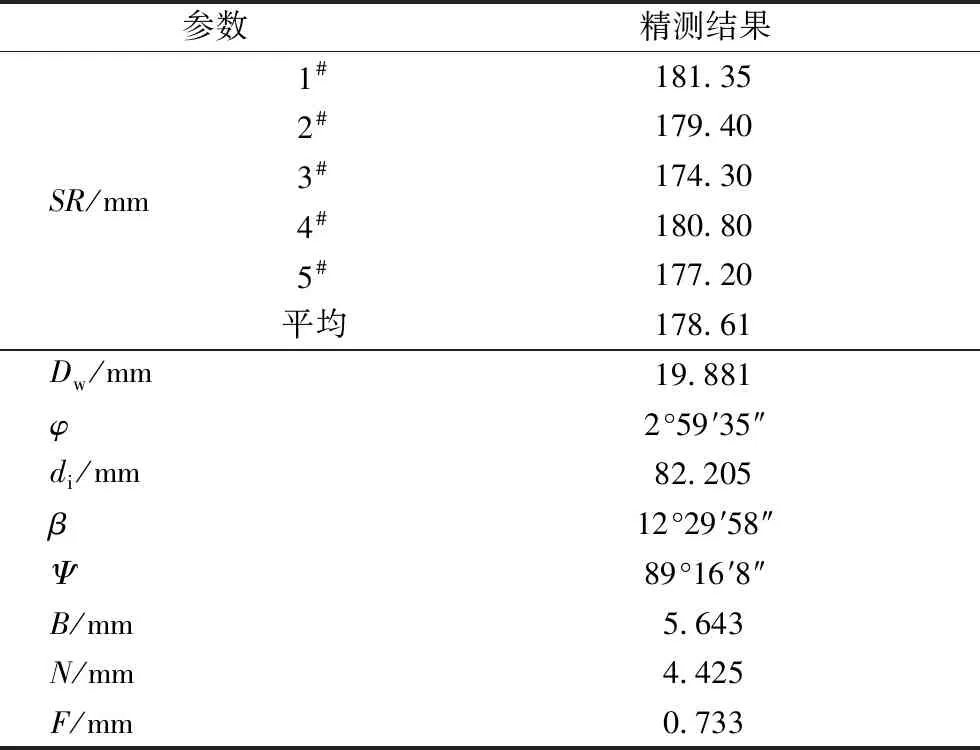
表1 滾子、內圈部分參數精測結果

5.2 接觸點位置的調整與控制

將接觸點控制在內圈大擋邊1/3～1/2之間的調整與控制方法：在Excel表格中輸入不同的Ψ值，當計算結果等于或接近兩控制點的數值(1/3處接觸點位置尺寸1.881 mm、1/2處接觸點位置尺寸2.821 mm)時，此時對應的Ψ角范圍即為生產過程內圈大擋邊精磨工序砂輪安裝所需控制的角度范圍。

對于接觸點位置尺寸精確計算，當Ψ輸入值為89°35′47″時，接觸點位置計算結果為1.88 mm；當Ψ輸入值為89°17′31″時，計算結果顯示為2.82 mm。因此，如需將接觸點控制在內圈大擋邊1/3～1/2之間，必須將Ψ角嚴格控制在89°17′31″～89°35′47″。

對于接觸點位置近似計算，當Ψ輸入值為89°35′45″時，接觸點位置尺寸計算結果為1.88 mm；當Ψ輸入值為89°17′31″時，計算結果顯示為2.82 mm。因此，如需將接觸點控制在內圈大擋邊1/3～1/2之間，必須將Ψ角嚴格控制在89°17′31″～89°35′45″。

比較接觸點位置的精確與近似計算結果，要將524467圓錐滾子軸承接觸點位置控制在內圈大擋邊1/3～1/2之間，實際控制的Ψ角范圍非常接近，從而進一步證明了接觸點位置尺寸精確計算與近似計算的差異極小，因此在生產過程中完全可以采用近似計算來代替精確計算，確定Ψ角所需要的控制范圍。

最后，利用計算結果指導內圈擋邊精磨工序砂輪角度的安裝與調整。針對不同的擋邊磨床，在砂輪安裝調整后，先試磨1～2個內圈大擋邊，采用輪廓儀精測Ψ，如果Ψ值在所計算的角度范圍內，則保持砂輪安裝角度進行內圈擋邊精磨加工；如果所測Ψ值不在所計算的角度范圍內，須調整砂輪安裝角度，直到Ψ值進入所計算的角度范圍為止，以確保批量軸承接觸點處于合理位置。

6 結束語

基于圓錐滾子軸承純滾動設計理論，利用滾子、內圈的幾何關系，對滾子球基面與內圈大擋邊的接觸點位置分別進行了精確、近似計算，通過實例證明精確計算與近似計算結果非常接近，因此，可以利用近似計算方法，只需精測軸承參數SR，Dw，φ，Ψ，B，N和F，并通過微調Ψ角度，在軸承生產過程中就可保證滾子球基面與內圈大擋邊的接觸點處于理想位置范圍。