地鐵隧道兩井聯系測量嚴密平差及軟件實現
范朋飛 石德斌
(鐵道第三勘察設計院集團有限公司,天津 300251)
地鐵隧道兩井聯系測量嚴密平差及軟件實現
范朋飛 石德斌
(鐵道第三勘察設計院集團有限公司,天津 300251)
介紹兩井聯系測量鋼絲投點法的工作原理與技術要點,依據無定向導線的特性采用附有參數的條件嚴密平差,最后通過程序實現數據自動化處理,并結合具體工程進行驗算分析。
聯系測量 無定向導線 平差 軟件
地鐵建設測量中聯系測量始終發揮著至關重要的作用,通過它可以建立地面控制點與地下控制點的對應關系,獲取地下控制點坐標及控制邊方位角,實現地下工程施工的精密控制。目前聯系測量方法較多,均有各自的特點和使用范圍,兩井聯系測量鋼絲投點法是一種過程簡單快捷、對現場生產影響較小的聯系測量方法,在地鐵聯系測量中得到很好的應用。
1 兩井聯系測量
兩井聯系測量鋼絲投點法是一種結合聯系三角形法和投點法各自特點形成的一種無定向聯系測量方法。相比一井聯系三角形法,大大拉長了兩根鋼絲的間距,減小鋼絲投點誤差對井下導線的橫向位置影響。如圖1是深圳地鐵9號線某車站的兩井聯系測量示意,井上通過近井控制點觀測角度和距離獲得兩鋼絲坐標,井下通過在控制點架設儀器觀測兩鋼絲,組成無定向導線,通過鋼絲坐標推算井下控制點坐標及控制邊方位角。
圖2為無定向附合導線通用示意,端點G1和G2為已知點,中間連接有n個待定點,必要觀測個數為2n,已有n個觀測角和n+1條觀測邊,因此剩余1個多余觀測條件,該條件即從G1點到G2點的坐標閉合條件。該導線中沒有方位角,很難列出條件方程,因此引入起始方位角參數,即引入起始邊G1-1的方位角T,通過方位角傳遞計算坐標增量,從而形成坐標閉合條件。基于以上分析,將采用“附有參數的條件平差”方法,對無定向附合導線進行嚴密平差。
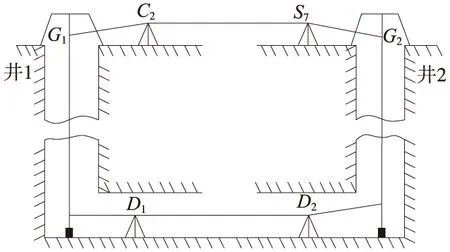
圖1 兩井聯系測量示意
2 無定向附合導線嚴密平差
2.1 近似坐標及方位角計算
以G1點為原點任意假定坐標系,設G1-1邊的方位角為0,則根據導線觀測角度,可推算其他邊的方位角,根據假定坐標系下的方位角和觀測距離可計算出G2點在假定坐標系中的坐標
(1)
可得假定坐標系和實際工程坐標系之間的夾角為
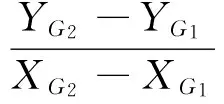
(2)
前面已經假設G1-1邊的方位角為0,因此T0即為起始邊G1-1的近似方位角,其余邊的近似方位角可用下式計算
(3)
其中,αSi為Si邊的方位角,βi-1為Si-1邊和Si邊的左夾角。
根據各邊的近似方位角和觀測距離可計算待定點的近似坐標
(4)
2.2 附有參數的條件方程
根據G1和G2的坐標閉合條件,可列下面條件方程
(5)
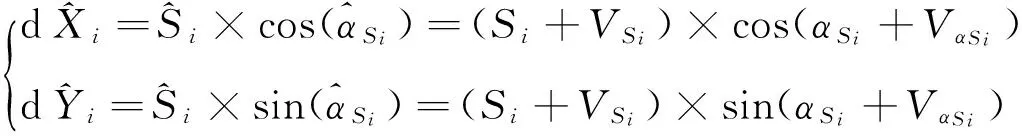
(6)
式中,VSi為邊長Si的改正數,VαSi為方位角αSi的改正數。
對式(6)進行線性化,得
(7)
由公式(3)可知
(8)
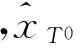
結合公式(3)和(8)可得
(9)
將(9)代入(7)得
(10)
將(10)代入(5)中整理后得
(11)
式中,WX和WY為坐標閉合差,具體形式為
(12)
附有參數的條件平差的一般形式為
(13)
將條件方程(11)化為矩陣形式為
(14)
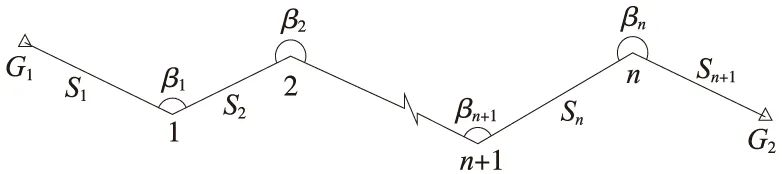
圖2 無定向附合導線示意
2.3 觀測值權的確定
無定向附合導線沒有方位角條件,因此無法通過方位角閉合差計算獲取測角中誤差mβ,通常依據儀器的測角精度、測回數及外部觀測條件等因素估算,測距中誤差可采用式(15)進行計算
(15)
式中,a為測距儀器的標稱固定誤差,b為比例誤差,Si為觀測的距離。
測角觀測精度相同,令測角中誤差mβ為單位權中誤差,則角度的權為Pβ=1,邊長的權為PSi=m2βm2Si。
3 軟件編程及算例分析
根據上面介紹的附有參數的條件平差理論,采用Visual Basic6.0開發工具,設計研制了“兩井無定向導線平差”軟件,該軟件集數據讀取、編輯、處理、繪圖、報表為一體,為數據處理提供了很好的幫助。
3.1 功能設計與數據處理流程
該軟件主要功能包括:數據讀取、編輯,數據平差處理,網圖繪制及保存,數據及平差報表的查看。軟件設計簡單快捷,無需安裝且支持多種操作系統使用。數據處理流程見圖3,軟件主界面見圖4。
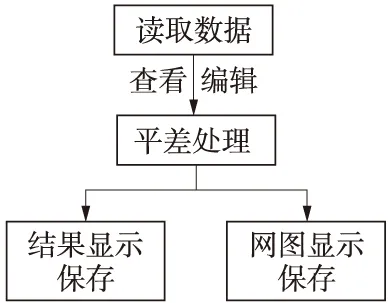
圖3 數據處理流程
圖4 軟件界面
3.2 算例分析
數據來自深圳地鐵9號線某車站的兩井聯系測量數據,如圖1所示,鋼絲坐標通過地面控制點C2和S7解算獲得,井下以鋼絲G1和G2為已知點,通過在D1和D2分別架設儀器,觀測相應角度和距離,組成無定向導線,解算地下控制點D1和D2的坐標及D1-D2邊的方位角。觀測數據見表1。

表1 聯系測量觀測數據記錄表
觀測值定權參照儀器標稱精度,本次工程中測距標稱精度為±(2+2×10-6D) mm,儀器標稱測角中誤差為±0.5″。使用編制的軟件對數據進行解算,得到坐標閉合差為Wx=-1.04 mm,Wy=-0.06 mm,相對閉合差為1/88 520<1/35 000(城市軌道交通精密導線測量技術要求),滿足地鐵聯系測量規范要求。
4 結論
通過對無定向導線嚴密平差理論的研究及軟件編程,并結合具體工程進行驗算,得到以下結論:
(1)兩井聯系測量大大拉長了鋼絲間距,減小了鋼絲投點誤差造成的橫向偏差。因此,在實際工程應用中應盡量將無定向導線布設成沿線路方向的直伸導線形式,以減小最終橫向貫通誤差。
(2)附有參數的條件平差在無定向導線平差中應用比較合理,起到了嚴密平差的效果。
(3)采用VB開發工具進行編程,界面可視化強,算法編寫方便,成圖簡單,在本次工程應用中發揮了很好的作用。
[1] 楊柳,左志剛.地鐵平面聯系測量方法研究[J].鐵道勘察,2012(3):14-16
[2] 武漢大學測繪學院測量平差學科組.誤差理論與測量平差基礎[M].武漢:武漢大學出版社,2003
[3] 羅三明,萬文妮,高培芝.盾構工程豎井聯系測量數據處理方法研究[J].大地測量與地球動力學,2007(5):123-127
[4] 何波,劉成龍,黃志偉,等.全站儀豎井聯系測量的平差計算原理及其精度分析[J].鐵道勘察,2010(3):17-20
[5] 張儉為.雙井定向的原理在隧道貫通測量中的應用[J].江西測繪,2008(3):63-64
[6] GB 50308—2008城市軌道交通工程測量規范[S]
[7] 姬曉旭,劉成龍,何波.豎井聯系測量的新方法及其應用[J].鐵道勘察,2009(5):14-17
[8] 李軍.豎井定向聯系測量新方法的應用研究[J].測繪通報,2005(8):44-46
TheRigorousAdjustmentandSoftwareofConnectionSurveyaboutTwin-wellintheMetroTunnel
FAN Peng-fei SHI De-bin
2014-06-30
范朋飛(1987—),男,2013年畢業于長安大學地質工程與測繪學院,碩士,助理工程師。
1672-7479(2014)05-0012-03
U452.1+3
: B

