基于尺度比確定工程橢球在隧道獨(dú)立控制網(wǎng)中的應(yīng)用

肖雁峰

(中鐵第四勘察設(shè)計(jì)院集團(tuán)有限公司，湖北武漢 430063)

基于尺度比確定工程橢球在隧道獨(dú)立控制網(wǎng)中的應(yīng)用

肖雁峰

(中鐵第四勘察設(shè)計(jì)院集團(tuán)有限公司，湖北武漢 430063)

為提高隧道獨(dú)立控制網(wǎng)的精度，減少隧道獨(dú)立控制網(wǎng)的投影變形，需要建立工程橢球。將求定的相對(duì)于實(shí)測(cè)邊長(zhǎng)的尺度比等價(jià)轉(zhuǎn)換為抵償投影面的高程值，從而求出工程橢球長(zhǎng)半徑，建立工程橢球，再在該工程橢球下進(jìn)行一點(diǎn)一方向平差，減少隧道獨(dú)立控制網(wǎng)的投影變形，提高隧道獨(dú)立控制網(wǎng)的精度。

投影變形 工程橢球 隧道獨(dú)立控制網(wǎng)

1 概述

隧道獨(dú)立控制網(wǎng)精度的高低，直接影響到隧道的貫通精度，要提高隧道獨(dú)立控制網(wǎng)的精度，則需要減少投影變形的影響。文獻(xiàn)[1]指出只要選擇合適的高程投影面進(jìn)行投影，則在該參考面上的長(zhǎng)度變形為零，文獻(xiàn)[2]認(rèn)為在一定精度范圍內(nèi)對(duì)較小的區(qū)域是可以的。文獻(xiàn)[3]在常規(guī)投影變形處理方法的基礎(chǔ)上，介紹了尺度強(qiáng)制約束法和投影面重新選擇兩種投影變形的處理方法，并通過(guò)試驗(yàn)證實(shí)了這兩種方法只能適應(yīng)較小的區(qū)域。隧道獨(dú)立控制網(wǎng)屬于較小的區(qū)域，文獻(xiàn)[3]中介紹的兩種投影變形處理方法適合于隧道獨(dú)立控制網(wǎng)，文獻(xiàn)[4]介紹的尺度強(qiáng)制約束法，當(dāng)約束條件較多時(shí)，顯示不出該方法的優(yōu)越性，但在隧道獨(dú)立控制網(wǎng)平差時(shí)，采用一點(diǎn)一方向平差，該方法平差約束條件較少，可有效減少地面網(wǎng)點(diǎn)的固有誤差對(duì)GPS網(wǎng)型的扭曲，不會(huì)改變平差后GPS網(wǎng)的相對(duì)關(guān)系。因此，在獨(dú)立控制網(wǎng)的工程橢球參數(shù)加入尺度比，可有效減少投影變形的影響。文獻(xiàn)[5]介紹了幾種建立獨(dú)立坐標(biāo)系的數(shù)學(xué)模型，通過(guò)幾種建立獨(dú)立坐標(biāo)系的數(shù)學(xué)模型比較分析，橢球膨脹法更適合于建立工程橢球基礎(chǔ)上的獨(dú)立坐標(biāo)系。

2 基于實(shí)測(cè)邊長(zhǎng)確定尺度比以及尺度比確定抵償投影面高程

設(shè)兩個(gè)已知點(diǎn)M、N坐標(biāo)值為(Xm、Ym)，(Xn、Yn)，其實(shí)測(cè)平距為Dmn，GPS控制點(diǎn)反算邊長(zhǎng)為Smn，則可確定該區(qū)域尺度比K為

(1)

式(1)便是相對(duì)于實(shí)測(cè)地面控制網(wǎng)的邊長(zhǎng)歸算尺度比。

綜合抵償投影面方法和尺度比強(qiáng)制約束方法的優(yōu)缺點(diǎn)，可以將相對(duì)于實(shí)測(cè)邊長(zhǎng)的尺度比殘差通過(guò)抵償投影面方式進(jìn)行處理。 邊長(zhǎng)投影變形ΔD為

(2)

實(shí)測(cè)邊長(zhǎng)歸算至參考橢球面上的變形為ΔS1。

(3)

則

(4)

為了對(duì)尺度比殘差進(jìn)行抵償，則抵償面高程值Hm可表達(dá)為

(5)

Hm就是基于尺度比殘差確定的抵償投影面高程值。

3 工程橢球參數(shù)計(jì)算

參考橢球面是一個(gè)橢球曲面，其不同位置的半徑不同，但橢球不同位置半徑可通過(guò)橢球參數(shù)確定，根據(jù)所確定的測(cè)區(qū)抵償面高程確定對(duì)應(yīng)的工程橢球參數(shù)，采用文獻(xiàn)[5]中介紹的橢球膨脹法進(jìn)行橢球長(zhǎng)半軸的計(jì)算，以WGS84橢球長(zhǎng)半軸為基準(zhǔn)，工程橢球長(zhǎng)半軸計(jì)算如式(6)所示

(6)

(7)

(8)

式中a84、e84——WGS84橢球的長(zhǎng)半軸和扁率；

Bm——工程測(cè)區(qū)的平均緯度；

Hm——基于尺度比殘差確定的抵償投影面高程值；

hi——i點(diǎn)的大地高；

Hi——i點(diǎn)的高程；

n——求算ζ的衛(wèi)星控制點(diǎn)與水準(zhǔn)同測(cè)點(diǎn)的個(gè)數(shù)；

N——工程測(cè)區(qū)中心的卯酉圈曲率半徑；

ζ——工程測(cè)區(qū)平均高程異常。

投影面選擇工程測(cè)區(qū)的平均高程面，中央子午線取隧道進(jìn)、出口的平均經(jīng)度。

(9)

4 施工坐標(biāo)計(jì)算

獨(dú)立控制網(wǎng)投影平面通過(guò)建立一個(gè)工程投影面，采用直接投影法進(jìn)行施工坐標(biāo)計(jì)算。直接投影法是以工程橢球?yàn)閰⒖紮E球，將無(wú)約束網(wǎng)平差WGS-84結(jié)果直接投影至工程橢球相切的高斯平面上(該平面的高程與工程平均高程相等)。

(10)

(11)

(12)

式中x0、y0——施工坐標(biāo)系起算坐標(biāo)；

as——施工坐標(biāo)軸在施工坐標(biāo)系中的方位角；

ag——施工坐標(biāo)軸在高斯平面坐標(biāo)系中的方位角。

5 工程實(shí)例分析

清涼山隧道位于秦嶺北麓低中山區(qū)陜西省戶縣境內(nèi)，平均海拔1 400 m，最高海拔為1 580 m。起止里程DgK56+156～DgK68+709，隧道長(zhǎng)度12 553 m，是西成鐵路客運(yùn)專線中的一個(gè)長(zhǎng)大隧道。其中埋設(shè)GPS控制點(diǎn)26個(gè)，聯(lián)測(cè)CPⅠ、CPⅡ控制點(diǎn)4個(gè)。

施工坐標(biāo)計(jì)算采用工程橢球直接投影法一點(diǎn)一方向平差計(jì)算施工坐標(biāo)。以清涼山隧道出口左線中線投點(diǎn)(TY05-1A，直線上的中線點(diǎn))為坐標(biāo)起算點(diǎn)，其坐標(biāo)假定為：X0=40 000.000，Y0=60 000.000，將X軸(TY05-1A～TY04-2)的坐標(biāo)方位角設(shè)為 180°00′00″，坐標(biāo)投影面為隧道線路平均高程面(H=800 m)。用WGS-84無(wú)約束平差所獲得的大地坐標(biāo)，按(10)、(11)式計(jì)算GPS控制點(diǎn)在施工坐標(biāo)系中的坐標(biāo)。

(1)加入尺度改正與未加入尺度改正坐標(biāo)比較

從圖1可以看出，從隧道起點(diǎn)TY05-1A，隨著長(zhǎng)度增加，坐標(biāo)較差越來(lái)越大，隧道終點(diǎn)TY03-1加入尺度改正與未加入尺度改正的坐標(biāo)較差為北方向?yàn)?6.5 mm，東方向?yàn)?6.4 mm，因此尺度改正對(duì)隧道獨(dú)立控制網(wǎng)坐標(biāo)影響較大。

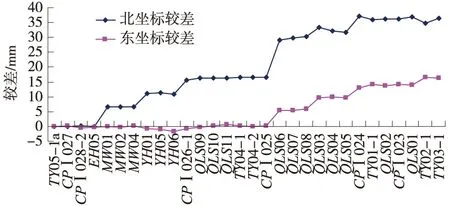
圖1 加入尺度改正與未加入尺度改正坐標(biāo)較差

(2)加入尺度改正與未加入尺度改正反算坐標(biāo)與測(cè)距儀實(shí)測(cè)邊長(zhǎng)比較

為了驗(yàn)證加入尺度改正的坐標(biāo)是否更接近實(shí)測(cè)邊長(zhǎng)值，進(jìn)行了一個(gè)實(shí)驗(yàn)，對(duì)能滿足通視條件的邊長(zhǎng)都利用測(cè)距儀進(jìn)行測(cè)量，并將邊長(zhǎng)投影改化。

將投影改化后的實(shí)測(cè)邊長(zhǎng)與加入尺度改正與未加入尺度改正坐標(biāo)反算邊長(zhǎng)進(jìn)行比較，通過(guò)43條坐標(biāo)反算邊長(zhǎng)和實(shí)測(cè)經(jīng)投影改化的邊長(zhǎng)進(jìn)行比較，從圖2可以看出，加入尺度改正的坐標(biāo)反算邊長(zhǎng)和實(shí)測(cè)經(jīng)投影改化的邊長(zhǎng)更吻合，未加入尺度改正的邊長(zhǎng)與實(shí)測(cè)經(jīng)投影改化的邊長(zhǎng)較差與邊的長(zhǎng)度有關(guān)，較差最大為-12.9 mm。

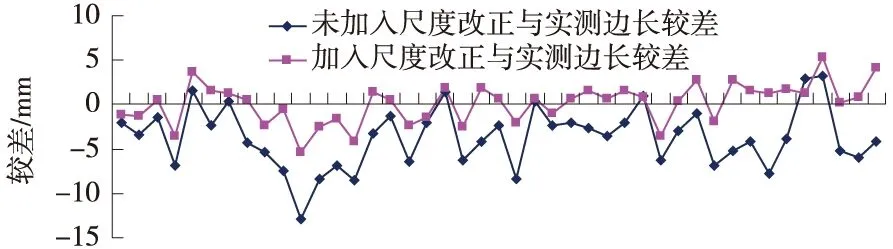
圖2 加入尺度改正與未加入尺度改正坐標(biāo)反算邊長(zhǎng)與測(cè)距儀實(shí)測(cè)投影改化邊較差

6 結(jié)論

經(jīng)理論和實(shí)踐證明，在隧道獨(dú)立控制網(wǎng)中加入尺度改正，可保證坐標(biāo)成果反算邊長(zhǎng)與實(shí)測(cè)邊長(zhǎng)一致，減少隧道獨(dú)立控制網(wǎng)的投影變形，提高隧道獨(dú)立控制網(wǎng)的精度。

[1] 孔祥元，梅是義.控制測(cè)量學(xué)(下)[M].武漢：武漢測(cè)繪科技大學(xué)出版社，1996：89-91

[2] 劉大杰，施一民.全球定位系統(tǒng)(GPS)的原理與數(shù)據(jù)處理[M].上海：同濟(jì)大學(xué)出版社，1997:56-58

[3] 范一中，王繼剛，趙麗華.抵償投影面的最佳選取問(wèn)題[J].測(cè)繪通報(bào)，2002(2)：20-22

[4] 高成發(fā).GPS工程控制網(wǎng)投影變形的處理[J].測(cè)繪工程，1999(4)：67-69

[5] 李祖鋒.基于尺度比確定工程參考橢球長(zhǎng)半徑[J].測(cè)繪通報(bào)，2010(增刊)：137-138

[6] 梁永.高速鐵路測(cè)量建立獨(dú)立坐標(biāo)系的數(shù)學(xué)模型[J].鐵道工程學(xué)報(bào)，2006(10)：33-35

[7] 楊柳.高鐵測(cè)量中投影變形處理方法探討[J].北京測(cè)繪，2012(1)：44-45

ApplicationofProjectEllipsoidBasedonScaleProportioninTunnelIndependentControlNetwork

XIAO Yan-feng

2014-01-10

肖雁峰(1979—)，男，碩士，工程師。

1672-7479(2014)02-0047-02

P282.2

： B