微積分及其在經(jīng)濟(jì)學(xué)中的應(yīng)用

沈奇

（黑河學(xué)院 數(shù)學(xué)系，黑龍江 黑河 164300）

微積分及其在經(jīng)濟(jì)學(xué)中的應(yīng)用

沈奇

（黑河學(xué)院 數(shù)學(xué)系，黑龍江 黑河 164300）

微積分的產(chǎn)生是數(shù)學(xué)發(fā)展史上一個(gè)重要的里程碑，在近代數(shù)學(xué)的發(fā)展中起到了重要的作用.微積分方法目前已被應(yīng)用于各個(gè)學(xué)科領(lǐng)域.本文對(duì)微積分進(jìn)行了簡單的介紹，并對(duì)微積分在經(jīng)濟(jì)領(lǐng)域的邊值問題、最值問題進(jìn)行了相應(yīng)的分析，給出了微分學(xué)和積分學(xué)在經(jīng)濟(jì)領(lǐng)域的應(yīng)用實(shí)例.

微積分；邊值問題；最值問題

1 微積分的產(chǎn)生及思想

“微積分”由微分學(xué)和積分學(xué)兩部分組成，自17世紀(jì)以來，通過科學(xué)家們對(duì)不同領(lǐng)域的課題進(jìn)行研究，使得微積分應(yīng)運(yùn)而生.微積分的產(chǎn)生通常可分為三個(gè)階段：極限概念的產(chǎn)生；求積的無限小法（分割、求和、取極限）；積分和微分的互逆關(guān).微積分的產(chǎn)生和發(fā)展構(gòu)成了近代數(shù)學(xué)的主要內(nèi)容，對(duì)數(shù)學(xué)的發(fā)展具有重要的意義.

微積分主要解決兩類問題，即變化率問題（微分問題）和積累問題（積分問題）.解決變化率問題的思想是，考察在某個(gè)點(diǎn)附近的小范圍內(nèi)，近似的以“不變代變”、“以靜代動(dòng)”，求得平均變化率.該平均變化率近似等于該點(diǎn)處的瞬時(shí)變化率.再將小范圍無限縮小而趨向于零，促使“近似”轉(zhuǎn)化為“精確”，從而求得函數(shù)在指定點(diǎn)處的變化率.

積分問題的基本思想是，先將整體化為有限個(gè)微小的局部，在每個(gè)局部“以直代曲”、“以不變代變”，再積零為整求和式，得到整體的近似值，最后，再使每一局部無限變小，通過求和式極限，促使“近似”轉(zhuǎn)化為“精確”,從而得到積累問題的準(zhǔn)確值[1,2,3].

微積分的產(chǎn)生、發(fā)展與實(shí)際問題緊密相連，其思想為函數(shù)類型的判斷、極值問題等提供了理論依據(jù)，并且在航海、天文學(xué)、物理學(xué)和經(jīng)濟(jì)學(xué)等領(lǐng)域得到了廣泛地應(yīng)用.

2 微分在經(jīng)濟(jì)學(xué)中的應(yīng)用

2.1 微分在邊際問題中的應(yīng)用

邊際問題是經(jīng)濟(jì)學(xué)研究的重要問題之一，比如邊際成本、邊際收入、邊際利潤等，在經(jīng)濟(jì)學(xué)角度看來都是十分重要的問題.

現(xiàn)假設(shè)經(jīng)濟(jì)函數(shù)y=f(x)，并且在定義域內(nèi)是可微的，那么有：

f'(x)稱為函數(shù)f(x)的邊際函數(shù)，表示因變量關(guān)于自變量的變化率，即經(jīng)濟(jì)變量的變化率.f'(x)在x0點(diǎn)處的函數(shù)值f'(x0)稱為邊際函數(shù)值，表示經(jīng)濟(jì)變量x在x=x0條件下改變一個(gè)單位，經(jīng)濟(jì)函數(shù)值改變f'(x0)個(gè)單位.因此，總成本函數(shù)的微分即為邊際成本、總利潤函數(shù)的微分就是邊際利潤，等等[4].

下面以邊際成本為例，分析微分在邊際問題中的應(yīng)用.

設(shè)某企業(yè)生產(chǎn)某種產(chǎn)品，其產(chǎn)量為q，生產(chǎn)總成本為C，C是關(guān)于q的函數(shù)，且函數(shù)關(guān)系式為：C(q)=0.02q3+3q+200，那么邊際函數(shù)為：C'(q)=0.06q2+3.

現(xiàn)假設(shè)產(chǎn)量為100，那么此時(shí)邊際成本為：C'(100)=0. 06×1002+3=603，其經(jīng)濟(jì)意義表示當(dāng)產(chǎn)量達(dá)到100時(shí)，若再增加一個(gè)單位的產(chǎn)量，總成本將會(huì)增加603，如果令產(chǎn)品的單位為p，當(dāng)p>603時(shí)，此時(shí)擴(kuò)大生產(chǎn)將會(huì)盈利；當(dāng)p<603時(shí)，擴(kuò)大生產(chǎn)將會(huì)導(dǎo)致虧損.

2.2 微分在最值問題中的應(yīng)用

在自然科學(xué)、生產(chǎn)技術(shù)領(lǐng)域中，往往需要考慮如何在消耗最小的情況下，使得收益達(dá)到最大化的問題，在經(jīng)濟(jì)生產(chǎn)中，為了提高經(jīng)濟(jì)效益，這種關(guān)于優(yōu)化的最值問題也是十分重要的.例如利潤是衡量一個(gè)企業(yè)經(jīng)濟(jì)效益的重要因素，那么如何實(shí)現(xiàn)投入成本最低，而使得利潤達(dá)到最大呢？這節(jié)將討論在經(jīng)濟(jì)活動(dòng)中的最值問題.

定理 設(shè)函數(shù)f(x)在x0點(diǎn)的某一鄰域中有定義，f(x)在x0點(diǎn)連續(xù)且可導(dǎo)，若f'(x0)=0，且f(x)在x0點(diǎn)二階可導(dǎo)，那么有：若f"(x0)<0，則x0是f(x)的極大值點(diǎn).

對(duì)產(chǎn)品從生產(chǎn)到銷售的過程進(jìn)行核算時(shí)，都會(huì)涉及到成本、收益和利潤的問題.設(shè)產(chǎn)量為q，則總成本為C通常為q的函數(shù)，一般表示為：

其中F>0為固定成本，通常認(rèn)為與產(chǎn)量無關(guān)，為常數(shù)；V (q)·q為可變成本，V(q)是常值函數(shù)或常數(shù)，表示在生產(chǎn)q件產(chǎn)品的情況下，每生產(chǎn)一件產(chǎn)品的可變成本.設(shè)總收益為E(q)=p(q)·q，其中p(q)為價(jià)格函數(shù)，表示在生產(chǎn)q件產(chǎn)品的情況下，每件產(chǎn)品的銷售價(jià)格.

由1中討論可知C(q)、E'(q)分別為邊際成本和邊際收益，其經(jīng)濟(jì)學(xué)意義分別表示：在生產(chǎn)（銷售）q件產(chǎn)品的情況下，再生產(chǎn)（銷售）一件產(chǎn)品的成本（收入）.

令總利潤函數(shù)為P(q)，那么有：

P(q)=E(q)-C(q)

當(dāng)C(q)和E(q)的二階導(dǎo)數(shù)存在時(shí)，要使得利潤達(dá)到最大，由上述定理可知，應(yīng)滿足以下條件：

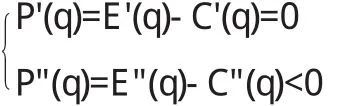
例 某產(chǎn)品的價(jià)格p(q)=α-βq（α,β>0,q<α/β），成本C(q) =F+vq（F,v為常數(shù)），那么利潤P(q)=E(q)-C(q)=-βq2+(α-v)q-f,要使利潤最大，即，則可得產(chǎn)量q=α-v02β（α-v>0保證企業(yè)盈利）.

3 積分在邊值問題中的應(yīng)用

在前面的討論中，我們采用微分的方法求解由總函數(shù)求邊值函數(shù)的問題.正如數(shù)學(xué)的角度一樣，微分和積分是一對(duì)互逆的運(yùn)算.本節(jié)我們將討論用積分法求解由邊值函數(shù)求解總函數(shù)的問題.

在經(jīng)濟(jì)問題中，通常會(huì)遇到對(duì)已知導(dǎo)數(shù)求原函數(shù)的問題，即求解常微分方程的問題.由邊值函數(shù)求解總函數(shù)一般采用不定積分；如果要求總函數(shù)在某個(gè)范圍的該變量，則采用定積分來求解.由于邊際收益、邊際成本、邊際利潤在產(chǎn)出量q的變動(dòng)區(qū)間[α,β]上的增量等于它們各自邊際在區(qū)間[α, β]上的定積分[5]，于是有:

例 設(shè)某產(chǎn)品的邊際成本和邊際收益為：C'(q)=0. 6q+10，E'(q)=30-0.2q

（1）產(chǎn)量由5增加到10時(shí)，總成本和總收益增加多少？

（2）已知固定成本為1萬元，產(chǎn)量為多少時(shí)總利潤最大，此時(shí)總利潤、總成本和總收為多少？

解（1）產(chǎn)量由100增加到500時(shí)總成本與總收益的增加量分別為：

（2）由邊際成本函數(shù)可得總成本函數(shù)：

由C(0)=1，代入上式得C=1，故總收益函數(shù)為

由邊際效益可得總效益函數(shù)：

由E(0)=0，代入上式得C=0，故總收益函數(shù)為

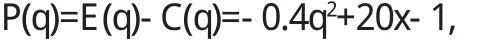
又由

可知，q=25時(shí)，總利潤最大.此時(shí)，總利潤、總成本和總收益分別為：

4 總結(jié)

在上述的討論中，本文只對(duì)微積分在經(jīng)濟(jì)研究中的部分應(yīng)用進(jìn)行了相應(yīng)的分析，而且，在經(jīng)濟(jì)領(lǐng)域中的很多類似的定量分析問題均可采用微積分的方法進(jìn)行求解，微積分在經(jīng)濟(jì)研究中具有重要的作用.不僅如此，數(shù)學(xué)思想在經(jīng)濟(jì)學(xué)領(lǐng)域的應(yīng)用，也使得金融數(shù)學(xué)學(xué)科得到了快速發(fā)展.利用數(shù)學(xué)思想對(duì)某些抽象的經(jīng)濟(jì)問題進(jìn)行分析，可使問題簡單化，易于理解.因此，將數(shù)學(xué)求解問題的方法應(yīng)用到經(jīng)濟(jì)領(lǐng)域具有重要的意義.

〔1〕陳紀(jì)修，於崇華，金路.數(shù)學(xué)分析[M].北京：高等教育出版社，2004.

〔2〕馬國良.微積分發(fā)展淺議[J].云南財(cái)經(jīng)學(xué)院學(xué)報(bào)，2000.

〔3〕李萬軍.微積分思想及其認(rèn)識(shí)[J].周口師范學(xué)院學(xué)報(bào)，2008.

〔4〕吳元芬.論微積分在經(jīng)濟(jì)分析中的應(yīng)用[J].數(shù)學(xué)學(xué)習(xí)與研究，2010(15).

〔5〕譚瑞林，劉月芬.微積分在經(jīng)濟(jì)分析中的應(yīng)用淺析[J].商場現(xiàn)代化，2008.

O172

A

1673-260X（2014）12-0006-02