分?jǐn)?shù)階微分方程積分邊值問題正解的存在性探究
冉營(yíng)麗,孟琳琳
(鄭州華信學(xué)院 基礎(chǔ)教學(xué)部,河南 鄭州 451100)
分?jǐn)?shù)階微分方程積分邊值問題正解的存在性探究
冉營(yíng)麗,孟琳琳
(鄭州華信學(xué)院 基礎(chǔ)教學(xué)部,河南 鄭州 451100)
本文針對(duì)分?jǐn)?shù)階微分方程積分邊值問題正解的存在性問題進(jìn)行了分析,希望所得結(jié)果能夠引起大家的關(guān)注和重視.
分?jǐn)?shù)階微分方程;積分邊值;問題正解存在性
0 引言
最近這些年,關(guān)于分?jǐn)?shù)階微分方程方面的問題逐漸成為許多專家和學(xué)者研究的熱點(diǎn)話題.分?jǐn)?shù)階微分方程較多的應(yīng)用在數(shù)學(xué)領(lǐng)域、流體流變學(xué)領(lǐng)域,其涉及到的理論知識(shí)十分復(fù)雜,關(guān)于分?jǐn)?shù)階微分方程解的存在性,很多專家和學(xué)者都進(jìn)行了大量的研究和試驗(yàn).
1 分?jǐn)?shù)階微分方程積分邊值問題正解存在性研究的意義
在現(xiàn)實(shí)的問題當(dāng)中,微分方程能夠更準(zhǔn)確的將化學(xué)、物理、生物等方面的問題做出合理的描述,而且在科學(xué)研究等領(lǐng)域,分?jǐn)?shù)階微分方程也具有十分廣泛的應(yīng)用.舉個(gè)例子來說,在對(duì)擴(kuò)音器進(jìn)行反饋和分析的時(shí)候,都能夠應(yīng)用到這種理論[1].但是對(duì)于邊值問題的提出和研究,主要是從應(yīng)用物理和應(yīng)用數(shù)學(xué)等領(lǐng)域得出的,除此之外,在熱傳導(dǎo)領(lǐng)域和流體學(xué)等領(lǐng)域?qū)τ诜謹(jǐn)?shù)階方程積分邊值的研究和應(yīng)用也十分廣泛.
2 微分方程邊值問題的研究
2.1 邊值問題的提出
給出一個(gè)微分方程:f(x,y,y',…,y(n))=0
在區(qū)間I上的點(diǎn)α1,α2,…,αk及值y(αi),y┡(αi),…,y(n-1)(αi)(i=1,2,…,k,k>1),對(duì)該方程設(shè)定一些條件,對(duì)于這個(gè)方程在I上面滿足這些條件時(shí)候的邊值和界值進(jìn)行求解.
當(dāng)該區(qū)間I的端點(diǎn)是K=2,α1、α2時(shí),就能夠證明,此時(shí)兩點(diǎn)的邊值問題.關(guān)于邊值問題的提出涉及到了諸多的領(lǐng)域和學(xué)科,不僅僅與物理學(xué)有著密切的關(guān)系,而且也涉及到了材料力學(xué)、流體力學(xué)和波動(dòng)力學(xué).此外,邊值問題在現(xiàn)代控制理論這一學(xué)科當(dāng)中也具有重要的研究?jī)r(jià)值.常微分方程能夠用來求解和進(jìn)行解析的類型非常少,基于這點(diǎn)原因?qū)呏祮栴}進(jìn)行求解也是具有相當(dāng)難度的,但是為了適應(yīng)實(shí)際問題的需要,采用近似求解也是一種不得已的方法.因此,我們首先需要回答這樣一些問題:邊值問題的解是否存在?是否惟一?這就是邊值問題的基本論題[2].
2.2 分?jǐn)?shù)階微分方程積分邊值問題的可解性研究
我們以射線法為例進(jìn)行研究,選擇一個(gè)微分方程的一般形式:

上述方程邊值的條件主要有三個(gè)類型,其中第一類是:

第二類是:

第三類是:
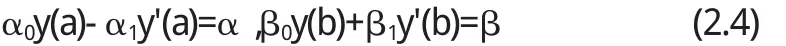
運(yùn)用數(shù)值法對(duì)邊值問題進(jìn)行計(jì)算求解,求解之前需要在理論上進(jìn)行驗(yàn)證,也就是說對(duì)邊值問題的解是否合理進(jìn)行解答.如果邊值問題的解不存在,那么采用數(shù)值方法來對(duì)數(shù)據(jù)進(jìn)行計(jì)算是沒有意義的.所以,下面給出一個(gè)邊值問題存在唯一解的充分條件,如下:

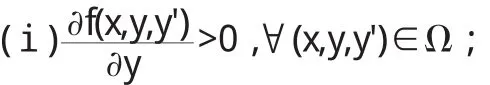

則邊值問題(2.1)-(2.4)的解存在且唯一[3].
3 預(yù)備知識(shí)
假如二階線性常微分方程邊值存在解,并且是唯一正解,并定義出現(xiàn)行算子L:Ly=-y"+p(x)y'+q(x)y.
這樣我們可以進(jìn)行考慮,需要對(duì)兩個(gè)線性微分方程初值問題進(jìn)行合理的解釋:

設(shè)u(x)和v(x)分別為上述兩個(gè)問題的解,那么就不難驗(yàn)證是更上一個(gè)問題的解,其中v(b)≠0.
這樣,通過以上的驗(yàn)證和描述,我們可以采用基于疊加原理的打靶式方法進(jìn)行研究,該方法的主要步驟如下:
1.根據(jù)邊值問題構(gòu)造相應(yīng)的初值問題;
2.分別求出兩個(gè)初值問題的解,這里面為u(x)和v(x);
3.以上述問題為例,將u(x)和v(x)進(jìn)行組合,最終所得到的函數(shù)y(x)就是上面邊值問題的解.
u(x)和v(x)都是二階常微分方程的初值問題,因此在進(jìn)行求解的時(shí)候需要將變量代換引入進(jìn)來,將這個(gè)問題進(jìn)行轉(zhuǎn)化,轉(zhuǎn)化為與該方程相適應(yīng)的一階方程的初值問題就能夠更好地解決.如令:
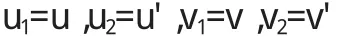
則該式可以寫成

該式可以寫成

這樣就可以利用Runge-Kutta方法求解.
對(duì)于更為普遍的線性邊值問題:

用基于疊加原理的打靶法的步驟為:
1.再重新構(gòu)造一個(gè)方程,創(chuàng)造出兩個(gè)與之相適應(yīng)的處置問題:

和

其中c0和c1是滿足條件c1α1-c1α0=1的兩個(gè)任意的常量[4].
2.對(duì)初值問題進(jìn)行求解,設(shè)它們的解分別為u(x)和v(x).
由此計(jì)算得到的函數(shù)y(x)就是這個(gè)方程的解.
此外,再講一個(gè)特殊方程的邊值問題,我們將其稱之為固有值問題,也有人稱之為本證值問題.這是一個(gè)含參數(shù)λ齊次邊值的問題,也就是說在這個(gè)方程里,無論是邊界條件還是微分方程都是齊次的,所以保證齊次邊值的問題具有非零解數(shù)值λ,就是特征值,對(duì)這些非零解本身就是一個(gè)特征函數(shù),也可以稱其為特征向量.
常型斯圖姆-劉維爾問題(簡(jiǎn)稱SL問題)是最典型的特征值問題:

在上述式子中,(α,b)是一個(gè)有限區(qū)間,1/p(x),q(x),1/r(x)是實(shí)的有界連續(xù)函數(shù).
常型問題一般都存在數(shù)不清的特征值,以λ0<λ1<λ2<…λn表示,每一個(gè)λn,都有一個(gè)對(duì)應(yīng)的非零解yn(x),我們將其稱之為特征函數(shù).{yn(x)}組成(α,b)上的完備正交系.對(duì)任意函數(shù)f(x),有特征展開式
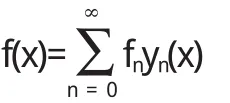
式中fn是f(x)的廣義傅里葉系數(shù),等于f(x)與yn(x)的乘積沿(α,b)的積分.當(dāng)f(x)滿足邊界條件,且f┡(x)絕對(duì)連續(xù)時(shí),展開式一致收斂.當(dāng)f(x)平方可積時(shí),展開式平方平均收斂.
斯圖姆曾經(jīng)證明了一個(gè)一般性的比較定理:如果g(x) 當(dāng)(α,b)不是有限區(qū)間,或者1/p(x),q(x),1/r(x)中至少有一個(gè)不是有界連續(xù)時(shí),就稱微分方程為奇型SL方程.這樣邊界條件的體罰和展開形式相對(duì)來說就較為復(fù)雜.按照H.外爾的理論來說,對(duì)于某個(gè)復(fù)數(shù)λ,微分方程的任何解都在b點(diǎn)鄰域平方可積,這樣一來,b屬于圓款;否則稱b屬于點(diǎn)款.而前面的方程,對(duì)于b點(diǎn)來說,需要提線性邊界條件;而對(duì)于后面的方程,只提平方可積條件就可以了.若α點(diǎn)為奇點(diǎn),也有同樣的分類.當(dāng)區(qū)間僅有一端為奇點(diǎn),特征展開式為 式中 φ(x,λ)為滿足α處邊界條件的解;ρ(λ)為不減函數(shù),稱為譜函數(shù).當(dāng)ρ(λ)為純階梯函數(shù)時(shí),展開式成為前述的級(jí)數(shù)形式(10),當(dāng)ρ(λ)沒有跳點(diǎn),展開式成為廣義傅里葉積分[5].對(duì)于區(qū)間兩端都為奇點(diǎn)的情形,展開式為 式中[ρij(λ)]稱為譜矩陣;φ1,φ2則是方程的線性無關(guān)解組. 4.1 當(dāng)f(x)為pm(x)eλx與eλx[pl(x)cosωx+pn(x)sinωx]時(shí),特解的形式及解法. 當(dāng)f(x)為pm(x)eλx與eλx[pl(x)cosωx+pn(x)sinωx]時(shí)特解的不同形式. 二階常系數(shù)非齊次線性微分方程的一般形式為 這里我們只討論f(x)為pm(x)eλx與eλx[pl(x)cosωx+pn(x) sinωx]型. 4.1.1 f(x)=pm(x)eλx 利用待定系數(shù)法求通解. 據(jù)分析可設(shè)特解y*=Qm(x)eλx,推得y*=xkQm(x)eλx其中Qm(x)是與Pm(x)同次多項(xiàng)式.k按λ是特征方程的單根、重根,不是根可取為1、2、0. 例: 求下列方程的特解或通解. 4.1.2 f(x)=eλx[pl(x)cosωx+pn(x)sinωx] 利用上面結(jié)果及歐拉公式、性質(zhì)推得 (1)當(dāng)λ+iω是特征根時(shí),k=1, (2)當(dāng)λ+iω不是特征根時(shí),k=0. 例: 求下列微分方程的特解 1.曲線上每點(diǎn)(x,y)處的切線在y軸上的截距為2xy2,且曲線過點(diǎn)(1,2),求此曲線方程. 解:設(shè)曲線的切線方程為Y-y=y'(X-x), 令X=0,于是切線在y軸上的截距為-xy'+y,從而 為貝努利方程,設(shè)u=y-1,上方程化為 其通解為,u=e-∫1xdx(∫2e∫1xdx d x+C)=x+C x 解: 方程兩邊對(duì)x求導(dǎo),得 為一階線性微分方程,解得 又因?yàn)閒(x)|x-0=1,代入上式,得C=2,因此所求函數(shù) 解:方程兩邊對(duì)x求導(dǎo),得f"(x)=6sin2x-f(x),即 此為二階常系數(shù)線性齊次方程,其對(duì)應(yīng)齊次方程的特征方程為r2+1=0,特征根為r1,2=±i,所以其對(duì)應(yīng)齊次方程的通解為 且非齊次方程的右端函數(shù)為3(1-cos2x),2i不是特征根,所以非齊次方程的特解可設(shè)為y*=A+Bcos2x+Csin2x,代入原方程,比較系數(shù)得A=3,B=1,C=0,所以 于是原方程所求通解為又因f(0)=1,f'(0)=1,代入上式,求得C1=-4,C2=1,因此所求函數(shù)為f(x)=sinx-4cosx+cos2x+3. 在本研究當(dāng)中,筆者主要針對(duì)微分方程邊值問題正解的存在性問題進(jìn)行了分析,同時(shí)研究了積分邊值問題的非線性方程分?jǐn)?shù)階正解的存在性,從中可以得出,積分邊值問題至少會(huì)存在一個(gè)正解,并且這是一個(gè)充分條件.通過本研究的論證可以得出,分?jǐn)?shù)階微分方程是存在正解的,但是關(guān)于正解的求法還需要更多的學(xué)者進(jìn)行討論和研究. 〔1〕高雷阜,王金希,吳洪濤.Banach空間中一類變分包含解的存在性和唯一性[J].遼寧工程技術(shù)大學(xué)學(xué)報(bào)(自然科學(xué)版),2012,14(02):154-155. 〔2〕夏順友,黃南京.到錐度量空間上的半連續(xù)集值映射的連續(xù)性 [J].遼寧工程技術(shù)大學(xué)學(xué)報(bào) (自然科學(xué)版),2012,11 (02):25-26. 〔3〕Hussein A.H. Salem. FRACTIONAL ORDER BOUNDARYVALUEPROBLEMWITHINTEGRALBOUNDARYCONDITIONSINVOLVING PETTIS INTEGRAL [J].Acta Mathematica Scientia. 2011,17(02):75. 〔4〕周昌宇,劉文斌.一類分?jǐn)?shù)階微分方程邊值問題單調(diào)迭代解[J].黑龍江科技學(xué)院學(xué)報(bào),2010,15(04):02-04. 〔5〕朱思念,王剛.一類非線性分?jǐn)?shù)階m點(diǎn)邊值問題可數(shù)多正解的存在性[J].四川理工學(xué)院學(xué)報(bào)(自然科學(xué)版),2011,11 (03):24. O175 A 1673-260X(2014)12-0008-03
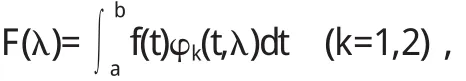
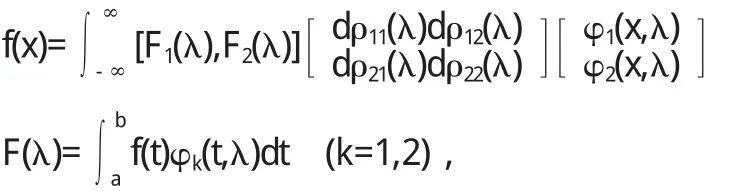
4 實(shí)際應(yīng)用


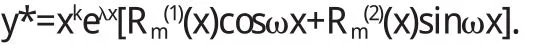






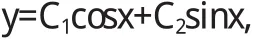

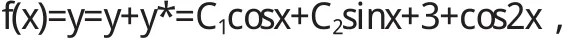
5 結(jié)語(yǔ)
 赤峰學(xué)院學(xué)報(bào)·自然科學(xué)版2014年24期
赤峰學(xué)院學(xué)報(bào)·自然科學(xué)版2014年24期
- 赤峰學(xué)院學(xué)報(bào)·自然科學(xué)版的其它文章
- 高校音樂教育教學(xué)管理系統(tǒng)的設(shè)計(jì)及實(shí)現(xiàn)
- 工業(yè)分析與檢驗(yàn)專業(yè)《藥物分析技術(shù)》項(xiàng)目化教學(xué)的應(yīng)用
- 英漢學(xué)習(xí)型雙語(yǔ)詞典的詞源信息設(shè)置介紹
- 大學(xué)英語(yǔ)學(xué)習(xí)者英語(yǔ)水平與隱喻能力的相關(guān)性研究
- 英語(yǔ)寫作中詞語(yǔ)搭配問題的調(diào)查與分析
- 個(gè)人知識(shí)管理在教育技術(shù)學(xué)專業(yè)人才培養(yǎng)中的策略研究
