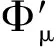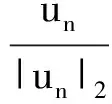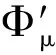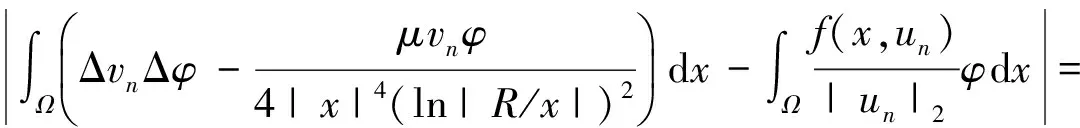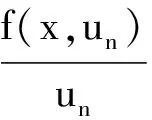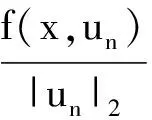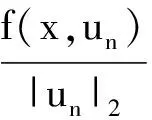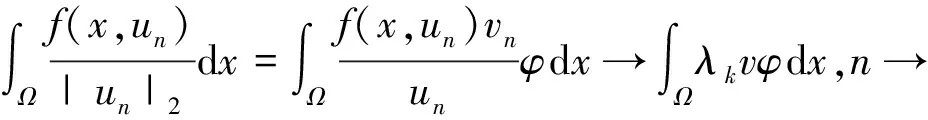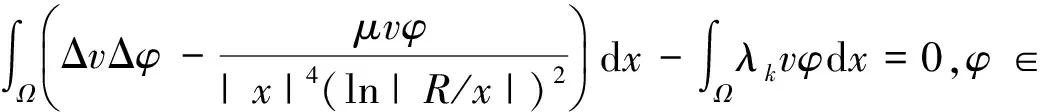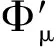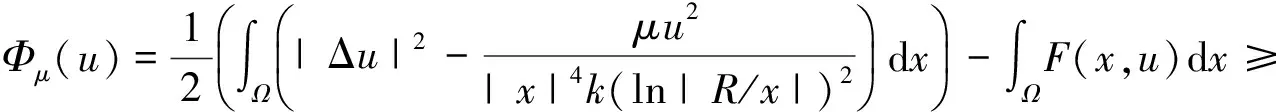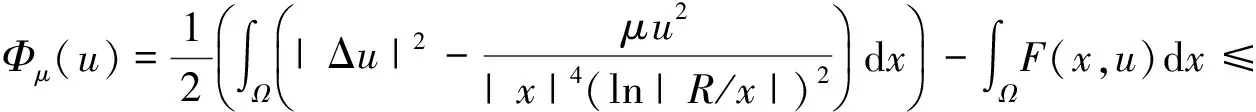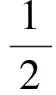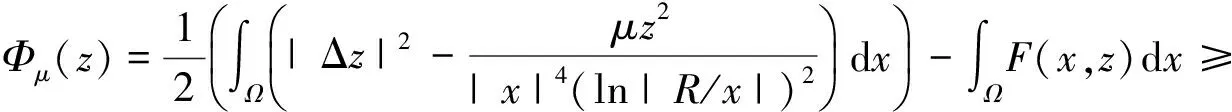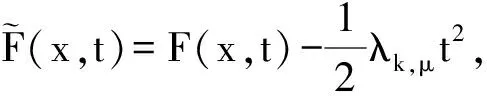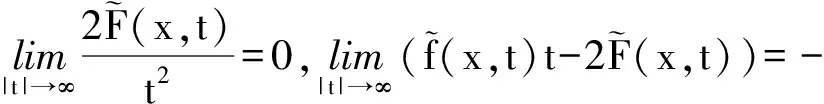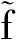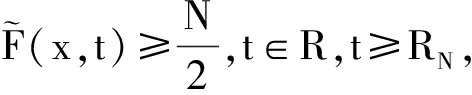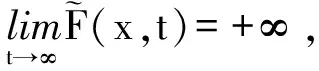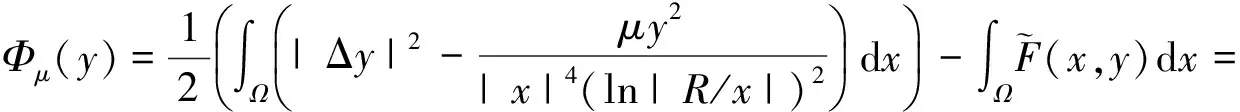含Hardy位勢雙調和方程解的存在性和多重性
劉春晗,王建國
(齊魯師范學院數學學院,山東 濟南 250013)
含Hardy位勢雙調和方程解的存在性和多重性
劉春晗,王建國
(齊魯師范學院數學學院,山東 濟南 250013)
利用山路引理及臨界群,在共振的情況下討論含Hardy位勢的雙調和方程,獲得了方程非平凡解的存在性和多重性.
Hardy位勢;山路引理;臨界群;非平凡解
1 預備知識
文獻[1-2]研究了特征值問題
(1)
其中R為常數,0≤q(x)≤1.若
這里Ω?R4,λ1是不可達的.
文獻[3]利用臨界點理論中的噴泉定理討論了方程
其中Ω?R4.得到了方程的非平凡解.
文獻[4]討論了方程
(2)
其中Ω?R4.當μ<1時,得到了方程(2)的非平凡解.
本文利用山路引理和臨界群,在f滿足無窮遠處共振的情況下,研究了方程(2)的存在性和多解性問題.此類問題在非共振的情況下研究得較多,而共振的情況研究得很少,而且我們的方法也不同于文獻[4-6].
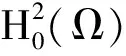
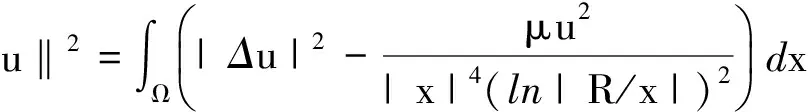
的完備化空間為H.易知H是按內積
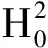
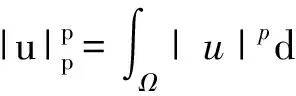
首先在空間H中討論以下的特征值問題非平凡解的存在性:
(3)
第一特征值定義為
其相應的特征函數記作φ1,μ.
第二特征值定義為
其相應的特征函數記為φ2,μ.
第n特征值定義為
其相應的特征函數記作φn,μ.
問題(2)的弱解就是泛函
的臨界點,其中
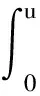
對于任意的φ∈H,
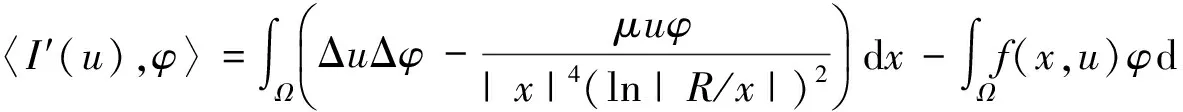
下面簡單介紹一下臨界群和Morse理論.更多的知識可參看文獻[6-8].
設H是Hilbert空間,泛函Φ∈C2(H,R)滿足(PS)(或(C))條件,Hq(H,Y)是具有整系數的q階奇異相對同調群.設u0是Φ的孤立臨界點,且Φ(u0)=c∈R.記
Φc={u∈H|Φ(u)≤c};K={u∈H|Φ′(u)=θ}.
我們稱群
Cq(Φ,u)=Hq(Φc,Φc{u0})(q∈Z)
為Φ在u0處的q階臨界群.若設K是有限集,稱
Cq(Φ,∞)=Hq(H,Φa)(q∈Z)
為Φ在無窮遠處點的臨界群,其中a 下面給出一些假設條件: 用到的定義和引理: 定義1[2]設Φ∈C1(H,R),稱Φ關于每一個c∈R滿足(C)c條件,若滿足 Φ(un)→c,(1+‖un‖)Φ′(un)→0(n→∞) 的任意數列{un}都有收斂子列;稱Φ滿足(C)條件,如果Φ關于每一個c∈R滿足(C)c條件. 引理1[4]若μ<1,特征值問題(3)有一個非平凡解φ1,μ. 引理2[4]若μ<1,當n→∞時,λn,μ→∞. 引理3[4]設H=Y?Z,Y=span{φ1,μ,φ2,μ,…,φk,μ},k≥2,μ<1,Z=Y⊥,則 定理1(山路引理)[9-11]假設φ∈C1(H,R)滿足 對某一個α<β,ρ>0,且u1∈H,‖u1‖>ρ.令 Γ={γ∈C([0,1],H):γ(0)=0,γ(1)=u1}, 且 則c≥β>0,且存在序列{un}?H,使得 φ(un)→c,(1+‖un‖)φ′(un)→0,n→∞. 而且,如果φ滿足(C)c條件,則c是φ的臨界值. 定理2[9]設H=X+?X-,Φ在X+上下方有界,且當‖x‖→∞時,Φ(x)→-∞,?x∈X-,ν=dimX-<∞.則Cμ(Φ,∞)0. 定理3 如果F(x,t)滿足假設條件(F1)—(F3),μ<1,則方程(1)至少存在一個非平凡解. 證明 (ⅰ) 證明I滿足(C)條件. 首先證明{un}是有界的.假設un滿足 vn?v與H,vn→v與L2(Ω),vn→v. a.e.x∈Ω. (4) 如果v(x)≠0,由假設條件(F2)可得 由在L2(Ω)中,vn→v,有 如果v(x)=0,有 所以對任意的φ∈L2(Ω),有 再由(4)式可得 由Fatou引理可得 另外 矛盾.故{un}是有界的. (5) 其中o(1)→0.當n,m→∞時,有 因此{un}在H上強收斂到u,故Φμ滿足(C)條件. (ⅱ)Φμ(u)滿足山路引理的條件.由假設條件(F1),(F2)可得,對任意的ε>0,存在C1>0,使得 取充分小的ε>0,使得A+ε<λ1,μ,利用Pioncaré不等式和Sobolev不等式,有 取‖u‖=r>0足夠小,可得Φμ|?Br≥α>0,其中Br={u∈H:‖u‖≤r}. 取ε>0充分小,使得λk,μ-ε>λ1,μ,我們有 因為?u∈Y,設u=tφ1,這里φ1相對于特征值λ1的特征函數,‖φ1‖=1,有 則存在e∈H,‖e‖>r,使得Φ(e)≤0. 所以Φμ滿足定理1的所有條件,則由定理1可得,方程(1)至少存在一個非平凡解. 定理4 如果f(x,t)滿足假設條件(F1)—(F2),(F3)′,則方程(1)至少存在兩個非平凡解. 證明 類似于定理3的證明可得,方程(1)存在非平凡解u1,并滿足 Cq(Φμ,u1)=δq1Z. (6) 另外,易知θ是Φ的局部最小值點,則 Cq(Φμ,0)=δq0. (7) 類似于定理3的證明可得,在(F2),(F3)′條件下,泛函Φμ滿足(C)條件. 設H=Y?Z,Y=span{φ1,μ,φ2,μ,…,φk,μ},k≥2,μ<1,Z=Y⊥.下面證明泛函Φμ在Z上下方有界.泛函Φm在Ψ上反強制,即當‖u‖→+∞,有Φμ(u)→-∞,?u∈Y. 取ε>0充足小,使得λk,μ+ε<λk+1,μ,利用引理4,?z∈Z,我們有 所以泛函Φμ在Z上下方有界. 因此,對任意的N>0,存在RN>0,有 對于t>0,我們有 對上式在[t,s]?[T,+∞)積分,可得 由上式,對y∈Y,且‖z‖→+∞,由引理4,有 由定理2可知, Cν(Φμ,∞)0. (8) 由(7),(8)兩式可知,Φμ有非平凡臨界點u2滿足 Cν(Φμ,u2)0. (9) 因為ν≥2,所以u1≠u2,故u1,u2都是方程(1)的非平凡解. [1] ADIMURTHI GROSSI M,SANTRA S.Optimal Hardy-Rellich inequalities,maximun principle and related eigenvalue problem[J].J Funct Anal,2006,240(1):36-83. [2] LIU XIANGQING,HUANG YISHENG.On sign-changing solution for a fouth-order asymptot-ically linear elliptic problem[J].Nonlinear Analysis,2010,72:2271-2276. [3] 謝朝東.平面中含Hardy位勢臨界參數的非線性橢圓型方程[J].應用數學學報,2006,29(6):1017-1023. [4] 陳志輝,沈堯天,姚仰新.R4中含位勢的非線性雙調和方程[J].數學年刊,2005,26A(4):487-494. [5] 伍蕓,韓亞蝶.一類臨界位勢非線性橢圓型方程非平凡解的存在性[J].山東大學學報:理學版,2012,47(10):1-5. [6] CHANG K C.Infinite dimensional morse theory and multipli solutions problems[M].Boston:Birkh? User,1993:32-43. [7] LIU J,SU J.Remark on multiple nontrivial solutions for quasi-linear resonant problem[J].J Math Anal Appl,2001,258:209-222. [8] MARINO B,ENRICO S.Semmilinear elliptic equations for beginners[M].London:Springer-Verlag,2011:46-48. [9] BARTSCH T,LI S J.Critical point theory for asymptotically quadratic functionals and applications to problems with resonance[J].Nonlinear Anal TMA,1997,28:419-441. [10] 萬保成,李健,王增輝.一類擬線性橢圓方程非平凡解的存在性[J].東北師大學報:自然科學版,2013,45(2):25-29. [11] PEI RUICHANG.Multiple solutions for biharmonic equations with asymptotically linear nonlinearities[J].Boundary Value Problem,2010,Article ID 241518:1-11. (責任編輯:陶 理) Existence and multiplicity of solutions for biharmonic equation with Hardy potential LIU Chun-han,WANG Jian-guo (School of Mathematics,Qilu Normal University,Jinan 250013,China) By using mountain pass lemma and critical group,biharmonic equations with Hardy potential at resonance are discussed.It proves the existence and multiplicity of nontrivial solutions. Hardy potential;mountain pass lemma;critical group;nontrivial solution 1000-1832(2014)04-0030-06 10.11672/dbsdzk2014-04-005 2013-06-08 國家自然科學基金資助項目(10971179);山東省高等學校科技計劃項目(J02LI53);齊魯師范學院青年教師科研基金資助項目(2013L1306). 劉春晗(1981—),男,碩士,講師,主要從事非線性泛函分析及其應用研究. O 175.25 [學科代碼] 110·4710 A
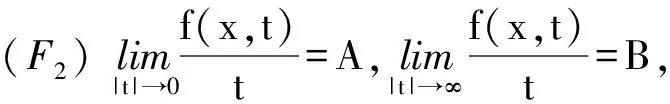
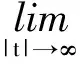
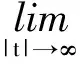
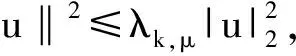
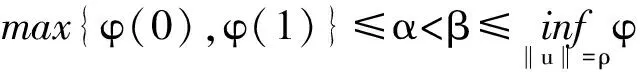
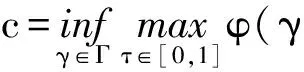
2 主要結果