生物氧化提金預處理過程參數間關系的辨識研究
李 泉
(中航飛機西安飛機分公司飛機設計研究院,西安 710089)
我國的難處理金礦資源儲量非常豐富,近來有業內專家普遍分析認為,國內的難處理金礦資源在探明的保有儲量中所占的比例約為1/3(1 000~1 200t左右),且主要分布于我國西南、西北和東北地區。目前處理難處理金礦的方法主要有3種,除了傳統的焙燒和加溫加壓氧化方法之外,自2000年開始生物氧化預處理-氰化預處理工藝在山東煙臺某企業正式投入使用。經過多年發展,我國建設的此類工廠,從數量和規模上,都躍居世界第一。生物氧化預處理工藝已成為我國解決難處理金礦預處理問題的重要手段[1]。生物氧化提金預處理技術可以解決常規選礦技術因回收率過低而無法工業利用的低品位金礦的選冶難題。
但是,生物氧化預處理技術的過程參數具有強耦合、強非線性特性,因而很難實現工業實時精確調控。為此,筆者提出一種依據遞推最小二乘法辨識生物氧化預處理過程參數間關系的方法,并通過方差分析驗證該方法的辨識精度。
1 工藝過程狀態參數分析①
生物氧化提金過程是典型的流程工藝,整個過程大致分為:原料調漿、再磨、濃縮脫藥、生物氧化預處理、生物氧化渣洗滌、壓濾、洗滌液中和、中和渣壓濾及中和渣堆存等。其中生物氧化預處理過程是整個提金過程中最重要的環節,該過程直接影響著黃金的產量和質量。
影響生物氧化預處理過程的因素主要有:礦漿濃度、磨礦細度、Fe3+濃度、培養基、水系、酸堿度(pH值)、溫度及進風量等,其中可控因素有溫度、酸堿度(pH值)和進風量。溫度是氧化預處理過程中比較重要的參數,適宜的溫度能夠提高細菌的活性,但過高的溫度會殺死細菌,致使氧化預處理過程無法繼續進行[2];酸堿度(pH值)主要為細菌培養一個適宜的生存環境,合適的酸堿度能夠大幅提高細菌的活性;進風量影響著氧化槽內好氧菌的活性,進風量太大不經濟,而且會造成氧化槽內液面波動劇烈致使礦液溢出污染環境,進風量太小又無法保證細菌的需求,使得細菌活性降低。
可控參數直接影響著生物氧化預處理過程的好壞,對它們的控制尤為重要。但是這些參數間的關系具有強耦合性和強非線性特征,常規控制方法難以實現,因此對參數間的關系進行辨識,來輔助控制顯得至關重要。
2 遞推最小二乘辨識理論
生物氧化預處理過程會產生大量的在線和離線數據,由于檢測環境復雜、測量儀表或設備故障及人工取樣分析異常等因素的影響,數據中不可避免地會出現一些異常數據,這些異常數據會降低辨識精度,無法正確反映參數間的相關關系。筆者依據拉依達準則對異常數據進行濾除,為參數間的相關關系辨識提供數據基礎[3]。
最小二乘法(又稱最小平方法)是一種數學優化技術,它通過最小化誤差的平方和尋找數據的最佳函數匹配[4]。利用最小二乘法可以簡便地求得未知數據,并使得這些求得的數據與實際數據之間誤差的平方和為最小。最小二乘法還可用于曲線擬合。其他一些優化問題也可以通過最小化能量或最大化熵用最小二乘法來表達。但最小二乘法需要大量的計算機內存且估計參數不能自動跟蹤實時參數數據的變化,遞推最小二乘法很好地解決了這一問題。
2.1 最小二乘法機理
考慮輸入/輸出模型,并設C(z-1)=1,則有:
A(z-1)y(k)=B(z-1)u(k-d)+ξ(k)
A(z-1)=1+a1z-1+a2z-2+…+anaz-na
(1)
B(z-1)=b0+b1z-1+b2z-2+…+bnbz-nb
式中ξ(k)——白噪聲序列。
設已知系統階次,具體任務是根據兩側的輸入和輸出確定參數a1,a2,…,ana和b0,b1,…,bnb,由式(1)可得輸入/輸出模型為:
y(k)=-a1y(k-1)-a2y(k-2)-…-anay(k-na)+b0u(k-d)+b1u(k-d-1)+…+
bnbu(k-d-nb)+ξ(k)
=φT(k)θ+ξ(k)
(2)
φT(k)=[-y(k-1),-y(k-2),…,-y(k-na),
u(k-d),u(k-d-1),…,u(k-d-nb)]
θT=[a1,a2,…,ana,b0,b1,…,bnb]
式中φT(k)——觀測量,且φT(k)∈R1×(na+nb+1);
θT——待估參數變量,且θT∈R1×(na+nb+1)。
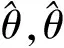
(3)
由式(3)可得,最小二乘法對模型參數的辨識只依賴輸入、輸出觀測變量數據。
2.2 遞推最小二乘法機理
由最小二乘法機理可知,最小二乘法需要大量的計算機內存且估計參數模型無法自動跟蹤輸入樣本數據的變化,實時性不好。遞推最小二乘法很好地解決了這一問題。
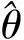

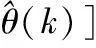
(4)
(5)
P(k+1)=[I-K(k+1)φT(k+1)]P(k)
(6)
P(k)=(ΦTΦ)-1,ΦT=[φ(1),φ(2),…,φ(k)]
式中K(k+1)——增益向量;
φ(i)——觀測向量。
3 生物氧化預處理過程參數相關關系辨識
3.1 數據預處理
由遞推最小二乘機理可知,在已知系統階次和輸入、輸出變量數據的條件下,借助遞推最小二乘法可以實現被研究對象系統的參數辨識。生物氧化預處理過程產生有大量的在線和離線數據,由于受復雜的檢測環境及人工分析取樣異常等因素的影響,數據中不可避免地含有一些異常數據。為了提高模型參數辨識的精度,有必要對異常數據進行剔除。
具有顯著誤差的異常數據常采用基于分布的方法來排除。基于分布的方法假定數據分布規律已知,且服從一種標準概率分布,異常值由樣本數據偏離參考分布的程度來定義[3],常用的方法有拉依達準則法、格拉布斯準則法、狄克遜準則法及肖維勒準則等[5]。拉依達準則是一種基于正態分布的異常數據檢測方法,通常又稱為3σ準則,由于使用和計算簡單而被廣泛應用。
筆者采用拉依達準則對原始數據進行處理,處理后共得到可用數據939條,見表1。
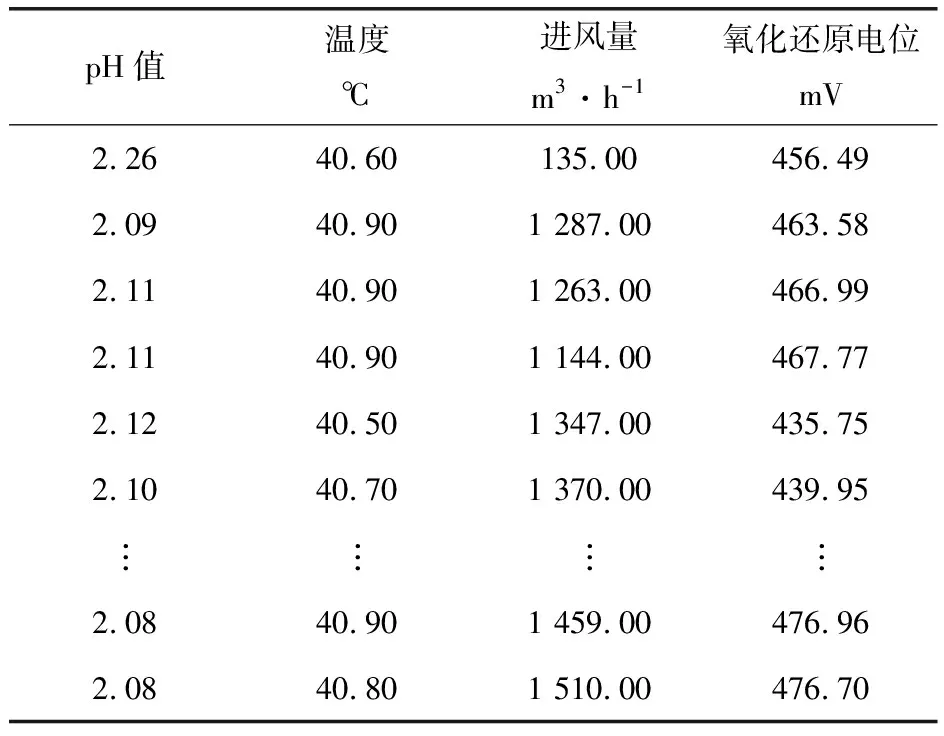
表1 拉依達準則處理后的數據
3.2 生物氧化預處理過程參數相關關系辨識
流程工業過程參數間的關系一般可用二階以上的函數描述[6],依據式(4)~(6)和表1中的數據,給定參數α=106,可得生物氧化預處理過程參數pH值與氧化還原電位間的函數關系的表達式為:
y=x3-2.17x2+130x-402.4
(7)
其中,自變量為pH值,因變量為氧化還原電位。
根據式(7)繪制pH值與氧化還原電位間的擬合相關曲線,由表1數據可以繪制出pH值與氧化還原電位間的實相關曲線,對比曲線如圖1所示。
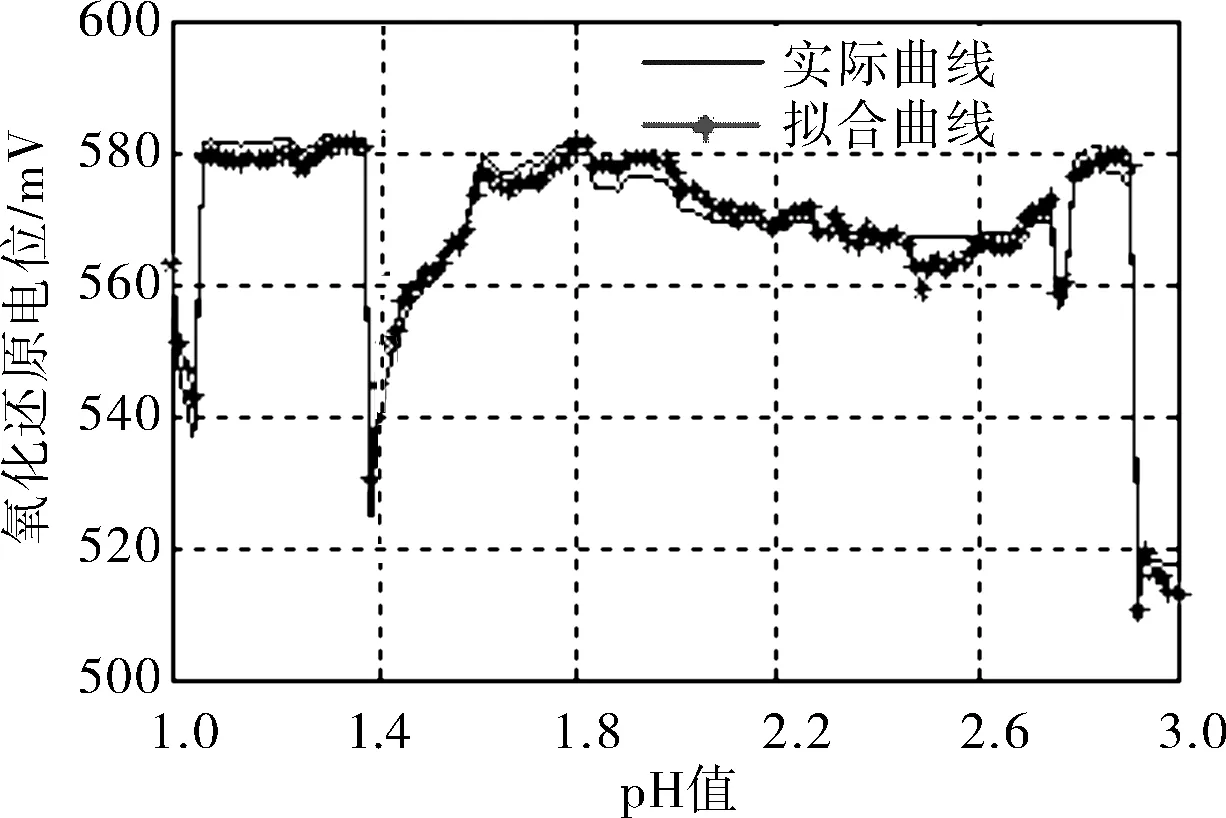
圖1 pH值、氧化還原電位相關關系曲線
同上,依據式(4)~(6)和表1的數據,給定參數α=106,可得生物氧化預處理過程參數溫度與氧化還原電位間函數關系的表達式為:
y=-x3+5.5x2-9.6x+5.6
(8)
其中,溫度為自變量,氧化還原電位為因變量。
根據式(8)繪制了溫度與氧化還原電位間的擬合相關曲線,由表1數據繪制了溫度與氧化還原電位間的實相關曲線,對比曲線如圖2所示。
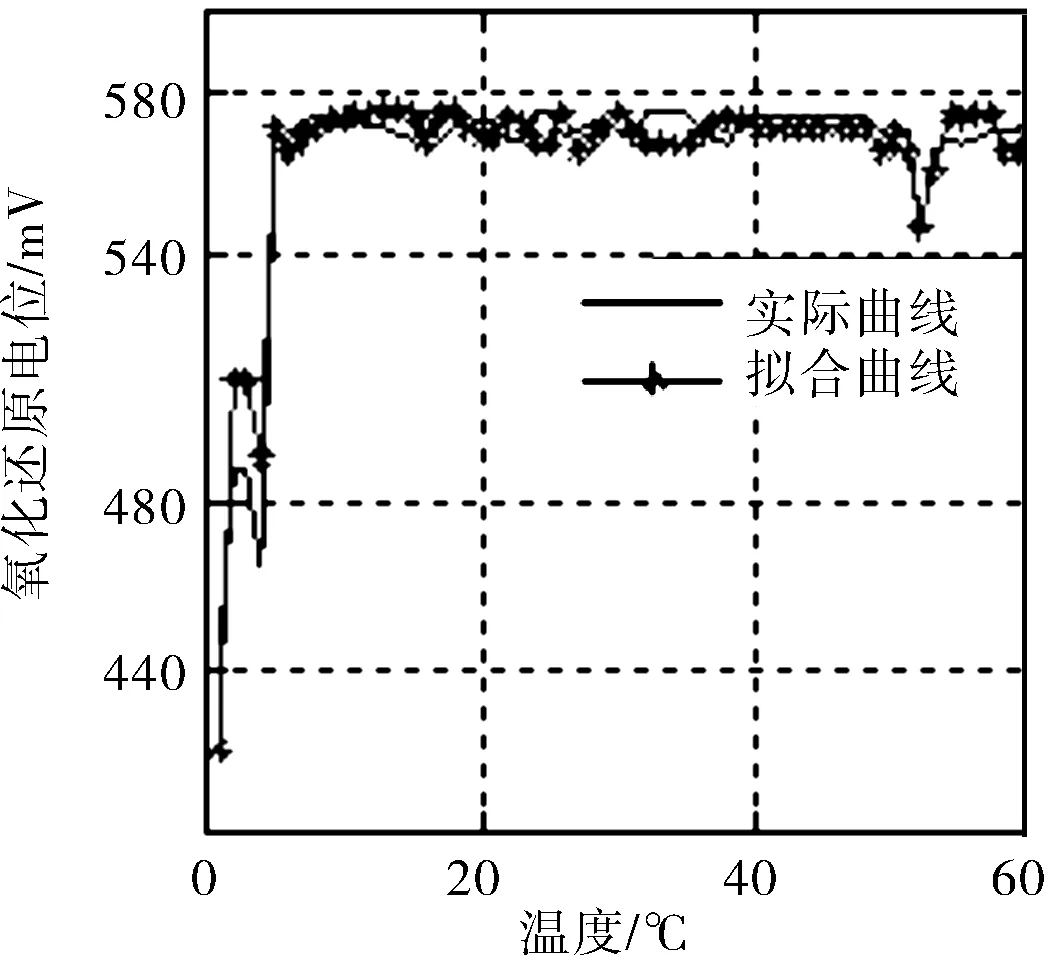
圖2 溫度、氧化還原電位相關關系曲線
4 方差驗證
辨識精度是衡量函數能否準確反映數據間相對關系的重要指標[7]。一般使用擬合值與實際值之間的方差來表征辨識精度。具體計算式如下:
(9)
式中y——實際值;

依據式(7)~(9)和表1的數據可以計算得到pH值與氧化還原電位的相關函數方差e1=3%、溫度與氧化還原電位的相關函數方差e2=2%。一般方差分析認為,方差在5%以內都是準確的[8,9]。因此,筆者依據遞推最小二乘法辨識生物氧化預處理過程參數間相關關系,所得結果準確、有效。
5 結束語
針對生物氧化預處理過程參數間關系具有的耦合和非線性強特性,而無法實時精確調控的問題,提出依據遞推最小二乘法,建立生物氧化預處理過程參數間關系辨識的新方法,得到了生物氧化預處理過程參數間相關關系的函數表達式,通過方差計算也驗證了所得函數表達式的辨識精度均滿足一般要求。

