有質量手性費米子的勢壘隧穿
潘林峰,曹振洲,程衍富
(中南民族大學 電子信息工程學院,武漢 430074)
費米子是自旋為半整數的粒子,比如自旋為1/2的電子就是最典型的費米子.電子通過勢壘的隧穿是量子力學中的基本問題,滿足Schr?dinger方程的非相對論電子通過勢壘時透射概率隨勢壘的高度和寬度指數衰減[1].因此電子完全通過極高和極寬勢壘的現象被認為是完全不可能的,然而1929年Klein[2]發現滿足Dirac方程的相對論電子可以完全隧穿勢壘,這個效應叫Klein隧穿.對Klein隧穿的理解來自量子場論[3].勢壘具有很強的電勢從而排斥電子而吸引正電子,導致在勢壘內部產生正電子態,它的能量與勢壘外面的電子匹配,越過勢壘的電子和正電子的波函數連續導致高隧穿效應.這里電子和正電子密切聯系,并由Dirac方程的不同分量來描述,這種性質通常叫電荷共軛對稱.雖然這個解釋能完全說明Klein隧穿,但要從實驗上觀察這個現象存在很大困難,即相對論電子的完全隧穿要求勢壘高度大于粒子的Compton波長,產生如此勢壘要求電場E>1016V/cm.以現在的技術手段幾乎不可能產生如此大的電場,因此這個效應從實驗上不可能被觀察,所以人們一直把這個現象稱為Klein佯謬.
2004年石墨烯的發現預言了兩維無質量Dirac電子的Klein隧穿[4],并且極容易地從實驗上觀察到這個效應[5],從而真正解決了Klein佯謬問題.石墨烯是具有兩個原子基(通常叫子格A和B)的二維晶體薄片[6].石墨烯蜂巢結構由2個三角布拉維晶格組成,因此載流子除了通常的電子自旋外(本文忽略),還有與子格自旋度相聯系的贗自旋.因為子格贗自旋,人們把波函數寫為子格空間的Dirac雙旋量,并且引入粒子的手性,即單層石墨烯中的準粒子是無質量手性費米子.后來發現在多層石墨烯系統中也能推廣手性概念,即準粒子為有質量的手性費米子.有質量手性粒子通過勢壘的行為與非手性粒子存在很大差異, 它們垂直通過勢壘前者表現為反Klein隧穿,后者出現振蕩隧穿[7, 8].本文重點討論有質量手性粒子,通過其在勢壘中的傳播來理解手性概念,并比較非手性粒子通過勢壘的隧穿行為.
1 贗自旋與手性

(1)
它是厄米和幺正算符,本征值為±1.不存在質量項時,螺旋算符與狄拉克-哈密頓量對易,因此與哈密頓量有共同的本征函數,這時我們把螺旋算符和手性看成相等. 比如質量近似為零的中微子為左手粒子,即它們的自旋與它們的動量反平行,反中微子是右手粒子,它的自旋與動量平行.單層石墨烯中的準粒子是無質量Dirac費米子,由石墨烯的晶格結構引入贗自旋σ.贗自旋來自晶格的兩個不等價子格A和B,因此可像自旋粒子一樣引入手性(螺旋性).因此石墨烯中準粒子的手性也可像方程(1)一樣定義為贗自旋在動量方向的投影[9],這里只要把自旋算符s改為贗自旋算符σ即可.對有質量的狄拉克粒子,需要推廣無質量粒子的手性概念.比如對多層菱形堆疊石墨烯系統,兩能帶低能哈密頓量近似為[10]:
HJ=ε(p)σ·nJ=ε(p)[cos(Jφ)σx+
sin(Jφ)σy],
(2)
其中nJ= -(cos(Jφ), sin(Jφ))表示贗自旋極化軸,在二維波矢平面上的極化角φ=arctan(ky/kx),波矢k與動量p的關系為p=?k.贗自旋矢量σ= (σx,σy)是兩維泡利矩陣.在上面的表示中,J表示石墨烯的層數,也叫手性自由度,它聯系各層的電子密度,比如對單層J= 1,對雙層J= 2,等.


圖1 費米圓上贗自旋矢量旋轉圖Fig.1 Diagram of pseudo-spin vector rotation on the Fermi circle
2 兩維有質量手性粒子的勢壘隧穿
兩維有質量手性粒子最簡單的模型出現在雙層石墨烯中[12].雙層石墨烯由兩個單層碳原子耦合而成,它的每層都為蜂巢結構,每層都有兩個不等價碳原子A和B. 兩層間不同堆疊構成不同的雙層系統,天然石墨剝離產生的雙層系統為Bernal堆疊,即上層的A2原子正好在下層B1原子的頂上.在多層石墨烯低能哈密頓量中,我們取J= 2,且ε(p) =p2/2m,這里有效質量m≈0.054me[13],me為祼電子質量.那么在能谷K點附近哈密頓量為[14]:
(3)
對K′點附近的低能哈密頓量只需作替換ky→-ky即可.由于我們研究的散射不考慮能谷混合, 今后只考慮對K能谷的散射.
雙層石墨烯系統的載流子是有質量手性費米子,它通過勢壘的行為與非手性粒子完全不同.下面考慮有質量手性粒子通過方勢壘的隧穿. 假定能量為E的手性費米子(電子)從左邊以角度φ入射到寬為D高為V0的方勢壘上,如圖2所示.
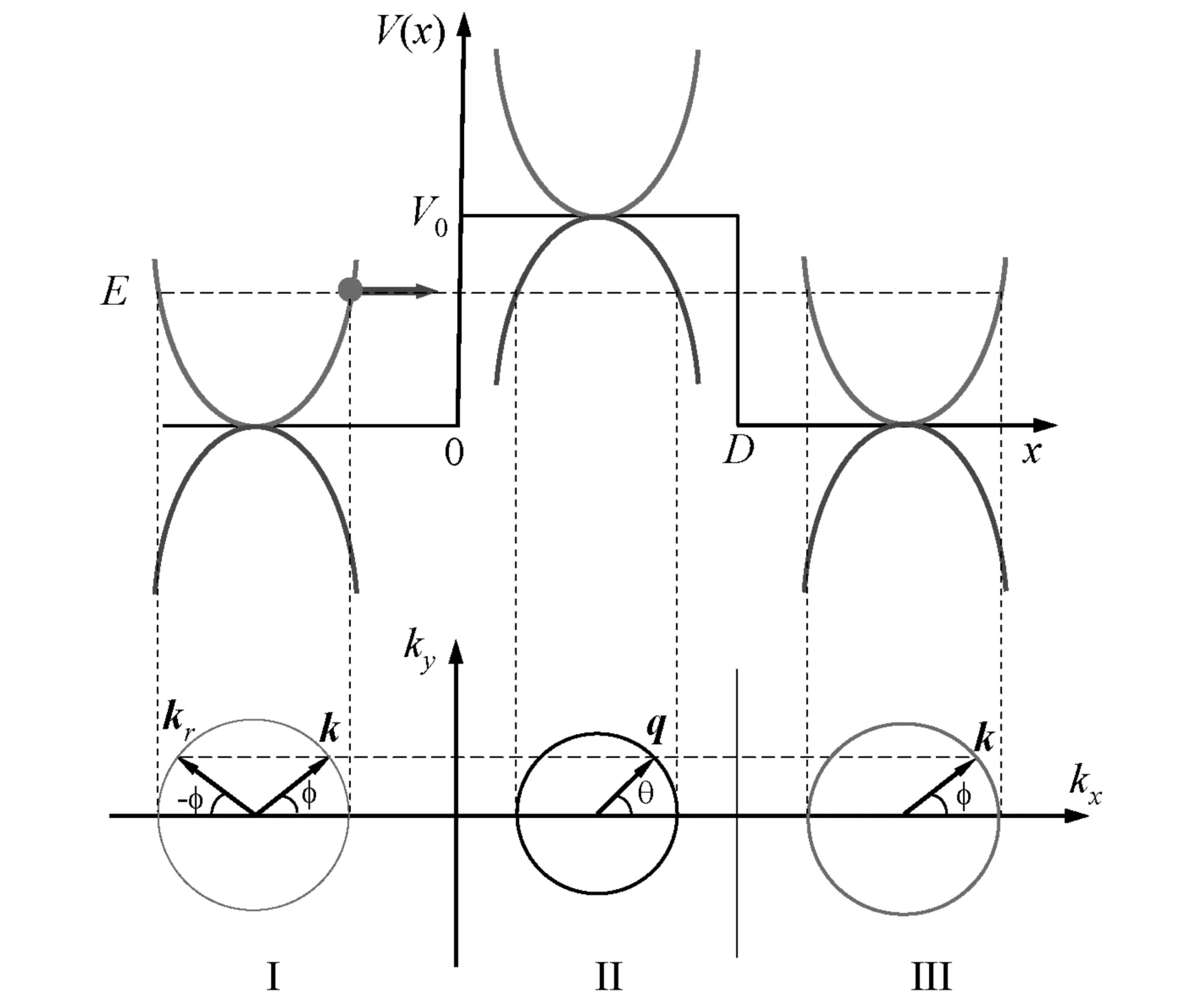
圖2 方勢壘和各區域波矢與散射角示意圖Fig.2 Schematic diagram of square barrier and regional wave vector vs the scattering angle
如果勢壘沿x為矩形并沿y軸無限長,則分段常數勢函數可表示為:
(4)
假定勢壘邊緣相當陡峭且在晶格尺度上光滑,則不引起能谷間散射,那么我們只需研究一個能谷K的散射. 由于勢函數與坐標y無關,則粒子的波函數可寫為ψ(r)=ψ(x)eikyy.二維矩陣表示中,無勢壘區域的波函數的x分量滿足本征值方程:
(5)
這里E是費米能.式(5)可寫為下面的2個微分方程:
(6)
(7)
由(6)、(7)消去ψ2(x)有:
(8)
方程(8)的解為傳播波解exp(±ikxx)或者指數增長(衰減)的倏逝波解exp(±kxx).把傳播波解ψ1(x)=e±ikxx代入(8)式有:
這里s表示能帶指標,E> 0,s= +1;E< 0,s= -1.即雙層石墨烯能量色散為二次關系,正如圖2所示的拋物線:
(9)
由式(7)有:
可得旋量的第二分量為:

(10)
同理對倏逝波有:


(11)



(12)
這里考慮只有電子傳播波入射,反射有傳播波和倏逝波.在0 (13) (14) 上述系數r1,r2,a,b,c,d,t1,t2都為復振幅,我們要求波函數和其導數在x= 0和x=D連續可求出這些系數,在計算過程中取s= 1,s′= -1. 在任意入射角φ下并不能得到透射系數的解析解,它需要用數值解來完成. 而正入射時,φ=θ=0,我們能求出透射系數的解析表示: (15) 并且t2=r2=a=b=0.那么透射概率為: (16) 如果D以nm為單位,方程(16)中雙曲函數的變量q量級達到107,則T以指數方式衰減很快,幾乎完全沒有透射. 雙層石墨烯在電子正入射時完全沒有透射,這通常叫反Klein效應.從波的邊界條件可知正入射時a=b= 0,即勢壘區域只有倏逝波通道,這種情況下與Schr?dinger粒子通過勢壘指數衰減完全相同.當然對斜入射粒子,勢壘中傳輸通道是傳播波和倏逝波的混合,倏逝波產生指數衰減,而向前和向后的傳播波通過Fabry-Pérot干涉產生共振透射[15]. 雙層石墨烯通過勢壘的Klein效應由其手性決定.對K能谷手性指標與能帶指標相同,即導帶手性為+1,贗自旋方向與波矢方向相同;價帶手性為-1,贗自旋與波矢方向相反. 粒子通過勢壘界面要求贗自旋守恒.比如對正入射(ky= 0),贗自旋只有x分量σx,贗自旋守恒使圖3中只能出現細黑箭頭所允許的傳輸過程,即雙層石墨烯中只允許出現反射傳輸.所以雙層石墨烯勢壘區域不可能出現傳播模,也就是說勢壘區域的空穴波矢不是實波矢-k而是虛波矢q=ik. 圖3 粒子電子正入射時贗自旋守恒示意圖Fig.3 pseudo-spin conservation Schematic diagram while normal incidence 為了與有質量手性粒子的勢壘隧穿進行比較,這里我們只能考慮非手性載流子無隙半導體,這有可能在某種異質結構中實現[16].這個系統的哈密頓量為: (17) 我們還是取勢函數在y方向平移不變,則波函數ψ(x,y)=ψ(x)eikxx.由波函數滿足的本征值方程有: (18) 即: (19) 設傳播波解為ψ(x)=e±ikxx,那么由(19)有: 這里s=±1分別表示導帶和價帶,波矢kx=kcosφ,ky=ksinφ,而φ為入射角. 這里qy=qsinθ=ky,θ是勢壘區域的折射角以及s′=sgn(E-V0).我們也只考慮入射電子的能量小于勢壘高度.對x< 0的無勢壘區域,波函數為: ψⅠ(x)=eikxx+re-ikxx, (20) 在0 ψⅡ(x)=aeiqxx+be-iqxx, (21) 同理x>D的無勢壘區域: ψⅢ(x)=teikxx, (22) 上述系數r,a,b,t都為復振幅.利用波函數其及導數在界面x=0和x=D連續可得出透射系數t: (23) 則透射概率T=|t2|為: T=|t1|2= (24) 下面通過圖解透射概率(24).由方程(24)知當滿足共振條件qxD=nπ,N=0,±1,±2,…,勢壘能完全透射,如圖4所示. 圖4表示斜入射時透射概率T與入射角φ的關系,其中E/V0=0.2(粗實線), E/V0=0.7(細實線),D=100nm.由圖可見當入射粒子的能量增加時,透射概率T與入射角φ呈明顯的不對稱性. 圖4 斜入射時透射概率T入射角φ的關系Fig.4 T-φ curves while oblique incidence 對正入射(φ = 0),透射概率T是勢壘寬度D的函數,如圖5所示. 圖5中E/V0= 0.3(粗實線), E/V0=0.2(細實線),從圖5知道, 有質量非手性粒子正入射時既不像無質量手性粒子一樣透射概率總為1[4],也不像有質量手性粒子那樣透射概率總為0,它的值在0到1之間振蕩.振蕩周期與勢壘高度V0,入射粒子能量E和勢壘寬度D都有關. 圖5 正入射時透射概率T與勢壘寬度D的關系Fig.5 T-D curves while normal incidence 本文研究了有質量手性和非手性費米子通過勢壘的隧穿概率.有質量手性粒子對應的系統為雙層石墨烯,這里由于層和子格引起贗自旋而粒子具有手性.對K能谷導帶中手性為+1,價帶中手性為-1,對K′能谷手性則相反.當滿足Dirac方程的粒子通過高度為V0的勢壘時,正入射粒子完全被反射,這就是反Klein隧穿.而斜入射的粒子由于在勢壘區域出現傳播和倏逝波的混合,倏逝波使透射振幅衰減而傳播波在界面的干涉產生Fabry-Pérot共振隧穿.兩維有質量無手性粒子可以出現在無隙半導體中,正入射時粒子完全隧穿隨勢壘寬度呈周期變化,斜入射也出現共振隧穿.它的表現與手性粒子完全不同,即不會出現Klein隧穿和反Klein隧穿. 參 考 文 獻 [1] Merzbacher E. Quantum Mechanics [M]. 2nd ed.New York: John Wiley & Sons Inc, 1970: 81- 114. [2] Klein O. Die reflexion von elektronen an potential sprung-nach der relativistischen dynamik von Dirac [J]. Z Phys, 1929, 53:157- 165. [3] 周邦融. 量子場論 [M]. 北京:高等教育出版社, 2008: 55-81. [4] Katsnelsio M I, Novoselov K S, Geim A K. Chiratun-nelling and Klein paradox in graphebne [J]. Nat Phys, 2006 , 2: 620- 625. [5] Huard B, Sulpizioet J A, Stander N,et al. Transport measurements across a tunable potential barrier in graphene [J]. Phys Rev Lett, 2007, 98: 236803. [6] Castro-Neto A, Guinea F, Peres N M R ,et al. The electronic properties of grapheme [J]. Rev Mod Phys, 2009, 81: 109. [7] Cao Zhenzhou, Cheng Yanfu , Li GuanQiang. Massive Dirac electron tunneling through a time-periodic potential in single layer grapheme [J]. Physics Letters A, 2011, 375: 4065- 4069. [8] Cao Zhenzhou, Cheng Yanfu, Li Guanqiang. Strain-controlled electron switch in grapheme [J]. Appl Phys Lett, 2012, 101: 253507. [9] Goerbig M O. Electronic properties of graphene in a strong magnetic field [J]. Rev Mod Phys, 2011, 83:1193. [10] Tworzyd lo J, Trauzettel B, Titov M, et al. Sub-Poissonian shot noise in graphene [J]. Phys Rev Lett, 2006, 96: 246802. [11] Park C-H, Marzari N. Berry phase and pseudospinwinding number in bilayer graphene[J]. Phys Rev B, 2011 , 84: 205440. [12] Edward McCann , Mikito Koshino. The electronicproperties of bilayer graphene[J]. Rep Prog Phys, 2013, 76: 056503. [13] McCann E, Abergel D S L, Falko V I. Electrons in bilayer graphene[J]. Solid State Commun, 2007, 143: 110. [14] Novoselov K S, McCann E, Morozov S V, et al.Unconventional quantum Hall effect and Berry′s phase of 2π in bilayer graphene[J]. Nature Phys, 2006, 2: 177. [15] Allain P E, Fuchs JN. Klein tunneling in graphene: optics with massless electrons [J]. Eur Phys J B, 2011, 83: 301-317. [16] Teissier R, Finley JJ, Skolnick MS, et al. Experimental determination of gamma-X intervalley transfer mechanisms in GaAs/AlAs heterostructures [J]. Phys Rev B, 1996, 54: 8329-8332.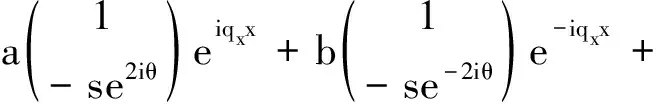


3 兩維有質量無手性粒子的勢壘隧穿


4 小結

