招生規模與教育質量模型的離散動力學分析

顧恩國，安樹庭，秦文釗

(中南民族大學 數學與統計學學院，武漢 430074)

2013年2月6日，國務院常務會議部署完善研究生教育投入機制，決定從2014年秋季學期起，向所有納入國家招生計劃的新入學研究生收取學費[1]. 該項政策的公布，立即在社會上引起了強烈的反響[2,3]，反映了教育系統可持續穩定發展的重要性與迫切程度. 隨著我國招生規模的迅速擴大，教學質量與招生規模的矛盾日益突出，尤其是教育質量，遭到來自多方的質疑[4]，因此眾多學者對教育系統的合理發展進行了探討，如招錄工作與獎學金制度[5]，招生規模的合理增長率區間估計[6,7]等，文獻[8-12]從不同側面(如招生規模、學費標準、政府投入等)建立線性和非線性動力系統模型，研究了不同情況下系統解的存在性與穩定性，為政府進行宏觀調控決策提供了相應的理論依據. 現有文獻的研究方法與結論對政府宏觀調控具有一定的參考意義，但均為連續模型，事實上，無論是招生、政府投入還是就業等行為都具有一定的周期性，因此離散動力學模型更符合實際.

為此，本文將考慮畢業生的就業成本，在適當的假設下建立招生規模與教育質量的二維離散動力學模型，描述兩者隨時間演化的規律，給出招生規模與教育質量可持續穩定發展的條件，為政府和高等院校進行宏觀調控提供相應的理論依據.

1 模型的建立

本文主要考慮招生規模與教育質量的非線性關系，用N(t)表示t時刻的招生規模，Q(t)表示t時刻的教育質量. 先考慮從t時刻到t+1時刻，招生規模的變化率：

(1) 假設教育資源充分，當教育質量增加時，招生規模可以適當地擴大(需要說明的是，盡管教育資源在現有條件下不是無限充分，此假設仍然可以揭示教育系統的一些內在變化規律)；

(2) 招生規模也與畢業生有關，如果畢業生的就業壓力過大，學校則應該降低招生規模，招生規模的變化與學生畢業時的就業成本成二次負相關[12]. 因此：

N(t+1)-N(t)=αQ(t)-λN2(t),

(1)

其中α>0為單位教育質量下應增加的招生規模，λ>0為畢業生的就業成本.

再考慮從t時刻到t+1時刻，教育質量的變化率：

(2)

其中β>0為單位招生規模下教育質量的相對改變量，反映教育質量對招生規模變化的敏感度.

根據上述說明，建立教育質量與招生規模的二維離散動力學模型如下：

(3)

2 非負平衡點的存在性

將模型(3)寫成映射動力系統的形式則有：

(4)

這里“′”表示時間增加一個單位算子，在實際中一般表示3～5年. 下面求系統(4)的平衡點，根據平衡點的定義，系統(4)的平衡點應滿足N′=N,Q′=Q，即為如下非線性方程組的解：

(5)

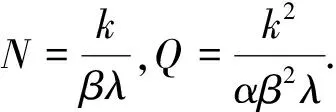
3 非負平衡點的局部穩定性

系統(4)的Jacobian矩陣為：

3.1 邊界平衡點E0的穩定性

邊界平衡點E0=(0,0)處的Jacobian矩陣為：

(6)

3.2 正平衡點E1的穩定性與分叉

正平衡點E1=(N*,Q*)處的Jacobian矩陣為：

(7)

由上述分析，我們有關于邊界平衡點E0=(0,0)和正平衡點E1=(N*,Q*)的穩定性和分叉的定理.

定理1

(1)無論參數α,β,k,λ如何變化，邊界平衡點E0=(0,0)恒不穩定；

(3)f(1)>0恒成立，因此系統(4)不會在E1處產生Fold分叉；

當k=2λ<2β時，1-f(0)=0且系統(4)有一對單位圓上的共軛復根，系統(4)將在E1處產生Neimark-Sacker分叉.

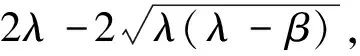
該定理說明政府為了引導良好的教育系統，應該一方面對教學質量進行適當的投入，另一方面還應降低畢業生的就業成本，可通過鼓勵畢業生自主創業，提供就業信息，引進需求企業等措施來實現.

4 數值模擬

首先驗證正平衡點E1的穩定性及Flip分叉. 固定參數α=1，β=0.75，λ=1>β，根據定理1的結論，當k<1時，正平衡點E1漸近穩定；當k=1時，系統在E1處發生Flip分叉.

圖1 系統(4)關于政府投入k的分叉圖，深色線表示教育質量，淺色線表示招生規模Fig.1 The bifurcation diagrams of the system (4) with respect to the investment of government k，the quality of education is represented in dark line, and the enrollment scale is represented in light line

如圖1(a)所示，當01時，正平衡點通過Flip分叉失去穩定性，招生規模與教學質量將出現周期或混沌波動，與定理1的結論剛好吻合.

接下來驗證正平衡點E1的穩定性及Neimark-Sacker分叉. 固定參數α=1，β=1.2，λ=1<β，根據定理1的結論，當k<2時，正平衡點E1漸近穩定；當k=2時，系統在E1處發生Neimark-Sacker分叉.

如圖1(b)所示，當02時，正平衡點通過Neimark-Sacker分叉失去穩定性，與定理1的結論剛好吻合.

為了確定在臨界狀態k=1時系統(4)的穩定性，需要使用中心流形定理[13]. 固定參數α=1，β=0.75，λ=1，當k=1時，正平衡點E1=(1.33,1.78). 對系統(4)作坐標平移變換，寫成矩陣形式為：

(8)

記f(u,v)=-0.69u2-0.75uv-0.20v2，g(u,v)=-0.34u2-0.74uv-0.30v2，設中心流形

Mc={(u,v)∈R2|v=h(u),h(0)=0,h′(0)=0,|u|<δ}，h(u)=b1u2+b2u3+o(u4)，有：

h(-u+f(u,h(u)))-0.33h(u)-g(u,h(u))=0.

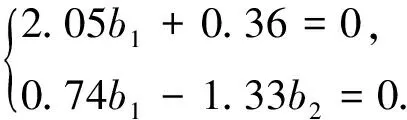
f1:u|→-u+f(u,h(u))=-u-0.69u2+0.132u3+o(u4),

限制，而f1的Schwarzian導數：

因此h(u)為穩定流形，則正平衡點E1在k=1時局部穩定.

5 結語和展望

本文研究了招生規模與教育質量可持續穩定發展的問題，建立了招生規模與教育質量的離散動力學模型，并對模型進行了非線性動力學分析，討論了正平衡點的存在性、穩定性及分叉. 結果表明：政府對教育資源的投入應綜合考慮教育質量對招生規模變化的敏感度以及畢業生的就業成本，教育質量穩定發展的一個充分條件是政府的投入k低于畢業生就業成本λ的2倍，在對教育質量進行投入的同時還應降低畢業生的就業成本.

本文僅考慮了單個學校的動力學模型，未考慮由于校際合作、競爭等情況給模型帶來的干擾. 將整個教育體系看成一個大系統，對有限的教育資源進行分配，并對招生規模進行估計將在后文中做進一步研究.

參 考 文 獻

[1] 佚名. 2014年秋季起研究生全自費，碩士學費不超過8000[EB/OL]. [2013-11-31].http://edu.163.com/13/0207/09/8N3OKCMC00293OM3_all.html.

[2] 佚名. 明年秋季起研究生全部自費打破30多年計劃體制[EB/OL]. [2013-11-31].http://yz.chsi.com.cn/kyzx/kydt/201302/20130222/390606520.html.

[3] 佚名. 研究生全自費難擋考研熱[EB/OL]. [2013-05-31].http://kaoyan.eol.cn/nnews_6152/20130506/t20130506_939089.shtml.

[4] 袁本濤，趙 偉，王孫禺. 我國研究生教育質量現狀的調查與研究[J].高等工程教育研究，2007，4：105-118.

[5] 李少俊. 經費是培養機制改革成功的關鍵[J].河南教育，2011，10：17-18.

[6] 馬以飛，白曉娟. 確定高等學校招生規模的BP神經網絡模型[J].遼寧工程技術大學學報，2004，23(2)：265-267.

[7] 謝作栩，黃榮坦. 中國高等教育規模發展宏觀調控模型研究[J]. 高等教育研究，2004，25(6)：18-24.

[8] 龐 偉. 微分函數在高校招生規模與就業率關系方面的應用分析[J]. 中國科技創新導刊，2011，7：43.

[9] 化存才. 高校畢業生就業率和招生規模的數學模型[J]. 工程數學學報，2005，22(8)：59-62.

[10] 化存才. 高校教育收費問題的微分方程模型與宏觀調控分析[J]. 云南大學學報：自然科學版，2008，30(1)：1-6.

[11] 化存才，陸啟韶，任 維. 數學應用工程研究[M]. 北京：科學出版社，2010.

[12] 化存才. 高校招生規模、政府投入和學費標準的三維動力學模型及政府調控[J]. 成都理工大學學報：自然科學版，2007，34(6)：657-660.

[13] Saber N E. Discrete Chaos [M]. New York：Chapman Hallcrc，2000.