非參數固定效應面板數據模型的約束剖面加權最小二乘估計

解其昌,賴紹永

(1.山東工商學院經濟學院,山東 煙臺 264005;2.西南財經大學經濟數學學院,四川 成都 611130)

1 預備知識

面板數據或縱向數據描述了跨越時間的個體信息,它包含截面和時間兩個方向維度．對比單純的時間序列數據或橫截面數據來說,面板的雙重維度不僅使其包含了每個個體更多的內容,而且有助于研究者發展更復雜的模型分析技術．隨著面板數據可獲得性的增長,面板數據的理論和應用研究變得越來越流行．關于參數面板數據模型的統計推斷和計量分析,Hsiao[1]和 Baltagi[2]給出了詳細的介紹和全面的回顧．

參數面板模型能夠簡明和清晰地描述出變量間的相互關系．然而,該類模型的最大缺陷就是需要很強的假設條件并且很容易產生模型錯誤設定的風險．如何彌補參數模型的這些不足,一個有效的備選方法就是引入非參數或半參數建模思想．本文就是基于這種思想,考慮下述非參數固定效應面板數據模型:

yij=αj+g(tij)+εij,i=1,…,n;

j=1,…,J<∞,

(1)

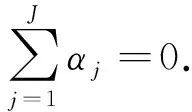
相比參數面板數據模型,非參數和半參數面板模型的研究還非常滯后．采用基于局部多項式近似的廣義估計方程技術,Lin等[3]檢驗了非參數平行面板數據模型的漸近性質,但是他們沒有給出估計量的收斂速度．Baltagi等[4]研究了隨機誤差服從獨立同分布的半參數固定效應面板數據模型的估計,卻沒有考慮誤差分布的異方差性．Su等[5]使用剖面似然法分析帶有固定效應的半參數面板模型,推導出了非參函數的漸近正態性,而并沒有得到固定效應的分布理論．通過一階差分方法,Henderson等[6]獲得了固定效應非參數面板數據模型估計的收斂率,但是由于計算程序復雜,沒有建立估計量的漸近正態分布性質．Qian等[7]運用邊際積分技術,討論了半參數固定效應面板數據模型的估計,然而該方法運算復雜且消耗時間．此外,文獻[8-11]也都對非參數面板模型進行了深入研究,但都沒有考慮異質信息或個體效應影響．

本文檢驗異方差非參數固定效應面板模型的一致估計．不同于傳統的一階差分方法,我們給出了使用約束剖面加權最小二乘技術估計該模型的詳細步驟．該方法的主要優點就是計算簡便以及容易實現．通過構造虛擬變量和引入局部線性近似的方法,不僅得到了模型中固定效應參數和非參數函數估計的表達式并且還推導出了估計量的漸近正態分布性質．同時,證明了參數和非參數估計量能夠實現相應的參數和非參數收斂率．

2 模型估計

若令ej是第j個元素等于1,其余元素是0的J×1維矩陣且記xi1=e1,…,xiJ=eJ、xi=(xi1,…,xiJ)T、yi=(yi1,…,yiJ)T、gi=(g(ti1),…,g(tiJ))T及εi=(εi1,…,εiJ)T,則方程(1)可以用矩陣重新寫為

y=xα+g+ε，

(2)

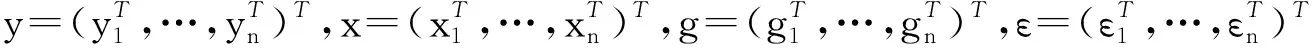
因為g(·)是一個未知的光滑函數,所以應用Taylor展開式來近似,即對tij臨域內的任意一點t有:

g(tij)≈g(t)+g′(t)(tij-t)=a(t)+

b(t)(tij-t)，

其中a(t)=g(t)和b(t)=g′(t)．

如果α已經被確定,那么γ(t)=(a(t),hb(t))T可以通過局部線性最小二乘來估計,即

Dtγ(t))TWt(y*-Dtγ(t))，

(3)

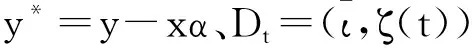
從式(3),解得

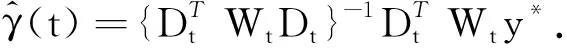
(4)

根據方程(4),知g的估計能夠表示為

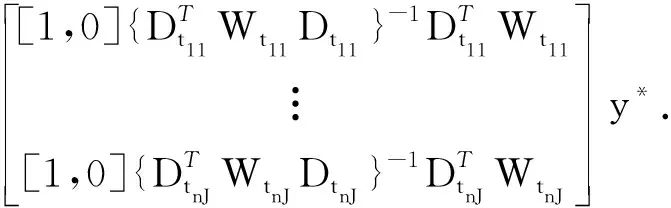
(5)

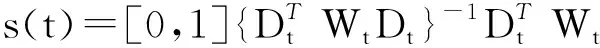
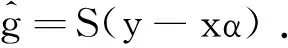
(6)

(I-S)y=(I-S)xα+ε,

其中I為nJ×nJ的單位矩陣．

接下來,使ι=(1,…,1)T是元素均為1的J×1維矩陣．因為隨機誤差εij服從異方差分布,所以傳統的同方差回歸技術不能被應用．因此,提出使用約束剖面加權最小二乘法來估計參數α．具體來說,固定效應α的約束剖面加權最小二乘估計為:

S)y-(I-S)xα)+2λιTα,

(7)

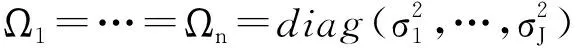
由目標函數Q(α,λ)的一階條件?Q(α,λ)/?α=0,推導出

xT(I-S)TΩ-1(I-S)xα+λιT-

xT(I-S)TΩ-1(I-S)y=0.

(8)

不言而喻,α的估計值為表達式(8)與方程ιTα=0的解．

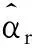
S)x]-1xT(I-S)TΩ-1(I-S)y-

(9)

進一步,把式(9)代入到ιTα=0中,得

{ιT[xT(I-S)TΩ-1(I-S)x]-1xT(I-

S)TΩ-1(I-S)y},

(10)

然后,再將式(10)代入到方程(9)中,有

S)TΩ-1(I-S)y-[xT(I-S)TΩ-1(I-

S)x]-1{ιT[xT(I-S)TΩ-1(I-S)x]-1ι}-1

{ιT[xT(I-S)TΩ-1(I-S)x]-1xT(I-

S)TΩ-1(I-S)y}ι.

(11)

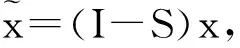
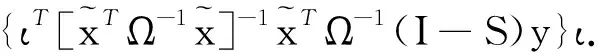
(12)

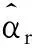
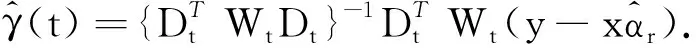
(13)

特別,非參函數g(t)估計的閉表達式為

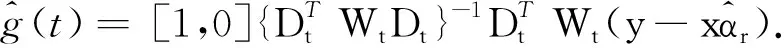
(14)

3 漸近性質

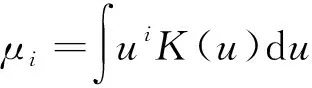
下面介紹一些假設條件,這些條件被廣泛使用于非參數面板數據模型的理論分析中[5,11].

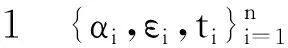
假設2 協變量tij存在緊支撐和具有二次連續可微的密度函數fj(·)．同時,密度函數fj(·),j=1,…,J有界且不等于零和無窮．

假設3 在緊支撐上,核函數K(·)對稱且一致有界以及函數g(·)存在連續有界的二階導數．此外,矩陣Γ是正定的．

假設4 當n→∞時,h→0,nh2→∞以及nh4=O(1)．

在闡述估計量的漸近分布定理之前,先給出一些引理．

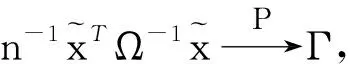
證明由假設條件1～4和大數定理知,對任意的λ>0,

(15)

通過矩陣運算以及應用式(15),得

(16)

同理,因為

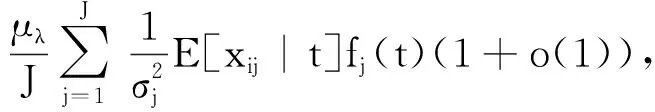
(17)

所以

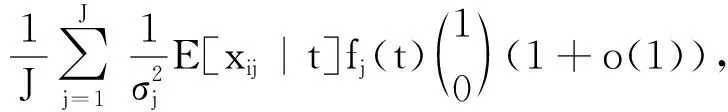
(18)

因此,

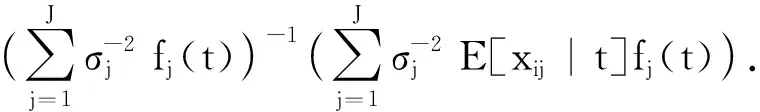
(19)

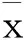
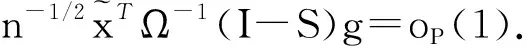
證明對任意的λ>0,注意到

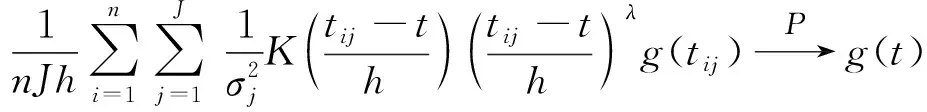
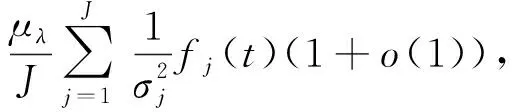
(20)

于是,

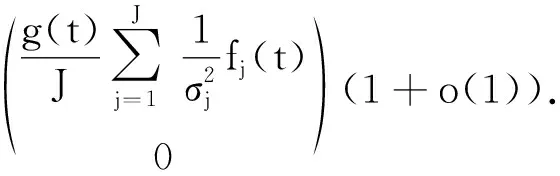
(21)

OP(1)oP(1)=oP(1).

證明類似于引理1的證明,知

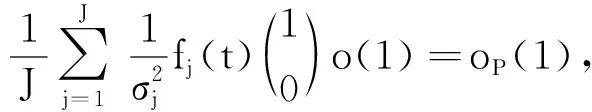
(22)

那么,s(t)ε=oP(1),這表明Sε=oP(1)．因此,

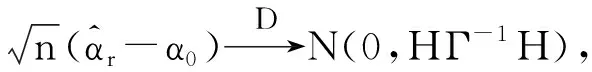
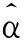
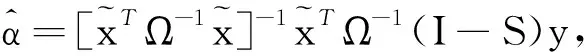
(23)

于是,結合式(12)和(23)知

(24)

因為ιTα0=0,所以由引理1和式(24),得

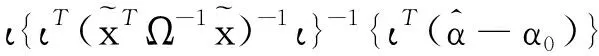
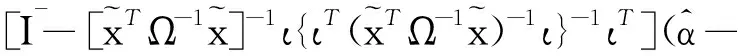
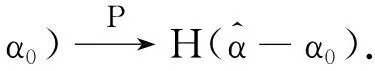
(25)

此外,由方程(23),有

C1+C2.

(26)

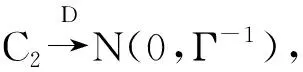
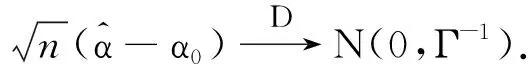
(27)

最后,由式(25)和(27)立即可以推出該定理．

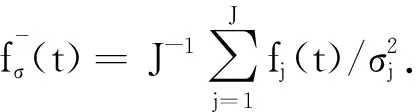
定理2 如果條件1～4成立,那么

證明由表達式(13),得

(28)

其中β=g″(t)h2/2以及Ψ=((t11-t)2/h2,…,(tnJ-t)2/h2)T．

這樣,根據式(28),有

K1+K2-K3.

(29)

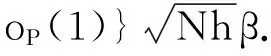
(30)

此外,注意到

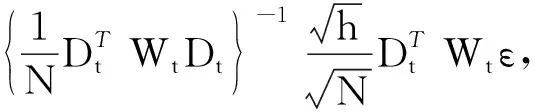
(31)

且

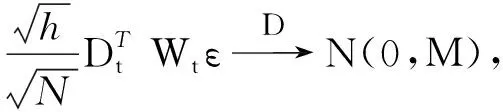
(32)

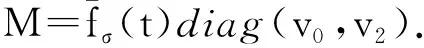
進一步,結合表達式(31)和(32)直接推出

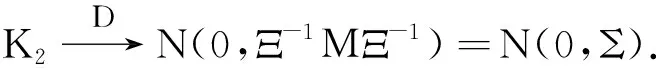
(33)

對于K3來說,有

(34)

最后,從方程(29)、(30)、(33)和(34),知該定理成立．

[1] Hsiao C.Analysis of panel data [M].Cambridge:Cambridge University Press,2003.

[2] Baltagi B H.Econometric analysis of panel data [M].West Sussex:John Wiley and Sons Ltd,2005.

[3] Lin X,Carroll R J.Nonparametric function estimation for clustered data when the predictor is measured without/with error [J].Journal of the American Statistical Association,2000,95:520-534.

[4] Baltagi B H,Li D.Series estimation of partially linear panel data models with fixed effects [J].Annals of Economic and Finance,2002(3):103-116.

[5] Su L,Ullah A.Profile likelihood estimation of partially linear panel data models with fixed effects [J].Economics Letters,2006,92:75-81.

[6] Henderson D J,Carroll R J,Li Q.Nonparametric estimation and testing of fixed effects panel data models [J].Journal of Econometrics,2008,144:257-275.

[7] Qian J,Wang L.Estimating semiparametric panel data models by marginal integration [J].Journal of Econometrics,2012,167:483-493.

[8] Jiang C R,Wang J L.Covariate adjusted functional principal components analysis for longitudinal data [J].The Annals of Statistics,2010,38:1194-1226.

[9] Ma S.Two-step spline estimating equations for generalized additive partially linear models with large cluster sizes [J].The Annals of Statistics,2012,40:2943-2972.

[10] Zhang X,Park B U,Wang J L.Time-varying additive models for longitudinal data [J].Journal of the American Statistical Association,2013,108:1360-1371.

[11] Yao W,Li R.New local estimation procedure for nonparametric regression function of longitudinal data [J].Journal of Royal Statistical Society:Series B,2013,75:123-138.