長(zhǎng)期軸向荷載作用下鋼骨混凝土柱的變形研究

陳周熠,吳建清,王 洋

(廈門(mén)大學(xué)建筑與土木工程學(xué)院,福建 廈門(mén) 361005)

鋼骨混凝土柱結(jié)構(gòu)是指在鋼骨周?chē)渲娩摻?并澆筑混凝土的柱結(jié)構(gòu),也稱為型鋼混凝土柱或勁性鋼筋混凝土柱．由于鋼骨混凝土柱結(jié)構(gòu)具有強(qiáng)度高,剛性大,以及良好的延性及耗能性能,在地震區(qū)的高層及超高層建筑中的應(yīng)用越來(lái)越廣泛．很多學(xué)者已開(kāi)展了關(guān)于鋼骨混凝土柱結(jié)構(gòu)的相關(guān)試驗(yàn)和理論研究[1-3],Shanmugam等[4]對(duì)此作了較深入的綜述．這些研究主要集中在鋼骨混凝土柱結(jié)構(gòu)的極限承載力、黏結(jié)強(qiáng)度和抗震性能等方面,但對(duì)于長(zhǎng)期荷載下由于混凝土的徐變和收縮引起的與時(shí)間相關(guān)的力學(xué)特性的研究還很少涉足．

徐變是在持續(xù)荷載作用下,混凝土結(jié)構(gòu)的變形將隨時(shí)間不斷增加的現(xiàn)象．收縮則是混凝土在硬化過(guò)程中,由于各種原因引起的隨時(shí)間變化而發(fā)生的體積縮小[5]．徐變和收縮會(huì)導(dǎo)致柱子在長(zhǎng)期荷載作用下持續(xù)增長(zhǎng)的變形．對(duì)鋼骨混凝土柱中徐變和收縮特性的理解,以及對(duì)由它們所引起的長(zhǎng)期變形的把握,將有助于在工程設(shè)計(jì)中對(duì)柱子的壓縮變形進(jìn)行精確分析,這一點(diǎn)對(duì)于高層建筑設(shè)計(jì)特別重要．

本文開(kāi)展了鋼骨混凝土短柱在長(zhǎng)期軸向荷載作用下變形發(fā)展的試驗(yàn)研究,并基于試驗(yàn)結(jié)果,討論了應(yīng)用現(xiàn)有的徐變和收縮模型,采用齡期調(diào)整有效模量法來(lái)模擬鋼骨混凝土柱在長(zhǎng)期軸向荷載作用下的變形發(fā)展的適用性．

1 試驗(yàn)研究

1.1 試件設(shè)計(jì)及材料特性

由于長(zhǎng)期加載試驗(yàn)要用到專門(mén)的徐變?cè)囼?yàn)機(jī),試件數(shù)量受到一定限制,本文共開(kāi)展了3個(gè)鋼骨混凝土短柱的長(zhǎng)期荷載試驗(yàn)．試件斷面形狀參見(jiàn)圖1,試件斷面尺寸為160 mm×160 mm,高度為410 mm．試件S1-N1和S1-N2的鋼骨采用80 mm×50 mm×4 mm (寬×高×腹板和翼緣厚度)的工字型鋼,試件S2-N1采用80 mm×50 mm×7.8 mm的工字型鋼．試件4角配置了直徑12 mm的變形鋼筋作為縱筋,采用直徑8 mm的光圓鋼筋作為箍筋,按間距100 mm布置．

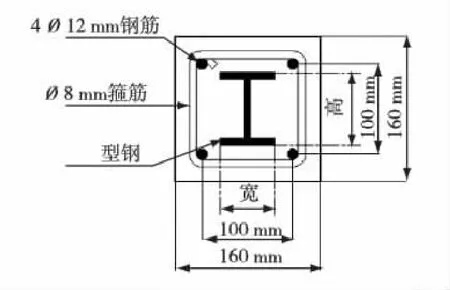
圖1 試件截面尺寸Fig.1 Cross section of test specimens

試件混凝土采用最大粒徑為10 mm的礫石作為粗骨料,歷時(shí)28 d，立方體抗壓強(qiáng)度為fcu=39.1 MPa,彈性模量為Ec=21 000 MPa．柱中的工字型鋼骨采用厚度分別為4和7.8 mm的鋼板加工而成,4 mm厚鋼板實(shí)測(cè)屈服強(qiáng)度為Fys=279 MPa,彈性模量為Es=204 000 MPa；7.8 mm厚鋼板實(shí)測(cè)屈服強(qiáng)度為Fys=266 MPa,彈性模量為Es=205 500 MPa．所用直徑12 mm變形鋼筋的實(shí)測(cè)屈服強(qiáng)度為Fyr=436 MPa,彈性模量為Esr=201 000 MPa；所用直徑8 mm光圓鋼筋的實(shí)測(cè)屈服強(qiáng)度為Fyh=325 MPa,彈性模量為Esh=200 000 MPa．

1.2 長(zhǎng)期荷載試驗(yàn)

為期202 d的長(zhǎng)期荷載試驗(yàn)是在徐變?cè)囼?yàn)機(jī)上進(jìn)行的,在試件混凝土齡期達(dá)到28 d時(shí)開(kāi)始加載．施加在試件S1-N1和S2-N1上的軸向長(zhǎng)期荷載分別為345和375 kN,相當(dāng)于試件在28 d齡期時(shí)的名義極限承載力的30%．選擇這個(gè)應(yīng)力水平,是因?yàn)楦邔咏ㄖ械闹釉诜燮诘恼９ぷ骱奢d下的軸壓比通常在0.3左右．為了考察軸向長(zhǎng)期荷載大小對(duì)于柱長(zhǎng)期性能的影響,試件S1-N2采用460 kN的荷載值,相當(dāng)于試件在28 d齡期時(shí)的名義極限承載力的40%．

試件加載期間的軸向應(yīng)變值,是通過(guò)監(jiān)測(cè)澆筑在試件側(cè)面上的標(biāo)距為150 mm的2個(gè)金屬預(yù)埋件之間的長(zhǎng)度變化來(lái)獲得的．長(zhǎng)度的測(cè)量和讀取采用千分表進(jìn)行,將千分表固定在其中一個(gè)預(yù)埋件上,千分表的滑桿則頂在固定于另一個(gè)預(yù)埋件的標(biāo)桿上,每個(gè)試件都在其中2個(gè)對(duì)應(yīng)側(cè)面上安裝了這套測(cè)量裝置．試驗(yàn)環(huán)境的溫濕度是通過(guò)溫濕度自動(dòng)測(cè)試儀進(jìn)行監(jiān)測(cè)采集．由于試驗(yàn)是在室內(nèi)進(jìn)行,監(jiān)測(cè)數(shù)據(jù)表明,在試驗(yàn)加載期間的溫濕度變化不大,因此可以不考慮溫濕度變化的影響．

1.3 試驗(yàn)結(jié)果

各試件長(zhǎng)期荷載試驗(yàn)得到的應(yīng)變變化曲線參見(jiàn)圖2．圖中表示的應(yīng)變值是荷載施加時(shí)的初始彈性應(yīng)變和后期隨時(shí)間增長(zhǎng)的應(yīng)變總和．如圖2所示,試件S2-N1,S1-N1 和 S1-N2在加載202 d時(shí)最終的應(yīng)變值分別達(dá)到了初始彈性應(yīng)變值的1.93，2.22和2.73倍,試驗(yàn)表明在長(zhǎng)期荷載作用下柱試件的變形增長(zhǎng)較為顯著．

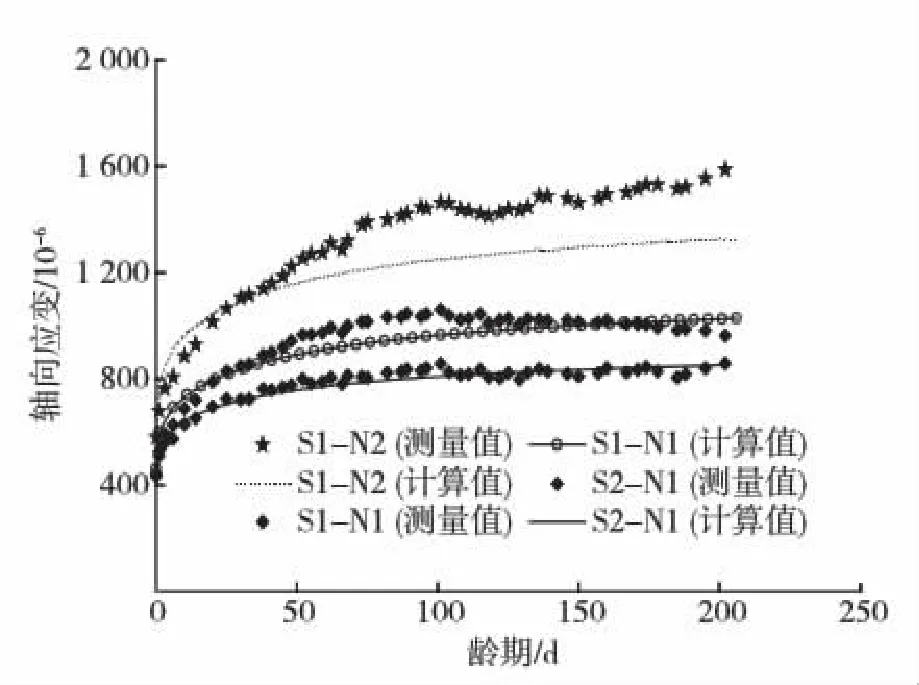
圖2 長(zhǎng)期荷載試驗(yàn)變形曲線Fig.2 Long-term strains during sustained load tests

如表1所示,試驗(yàn)參數(shù)包含了名義軸壓比(長(zhǎng)期荷載值與加載時(shí)名義極限承載力的比值)和鋼骨含鋼率(鋼骨斷面面積與柱截面面積的比值)．試件S1-N1和S2-N1軸壓比相同,鋼骨含鋼率不同,試驗(yàn)結(jié)果表明,隨鋼骨含鋼率的增加,長(zhǎng)期變形值有所降低．試件S1-N1 和S1-N2則有相同的鋼骨含鋼率和不同的名義軸壓比,結(jié)果表明,隨軸壓比的增加,長(zhǎng)期變形值相應(yīng)增大．由于徐變受混凝土應(yīng)力水平的影響很大,所以這一點(diǎn)很容易理解．

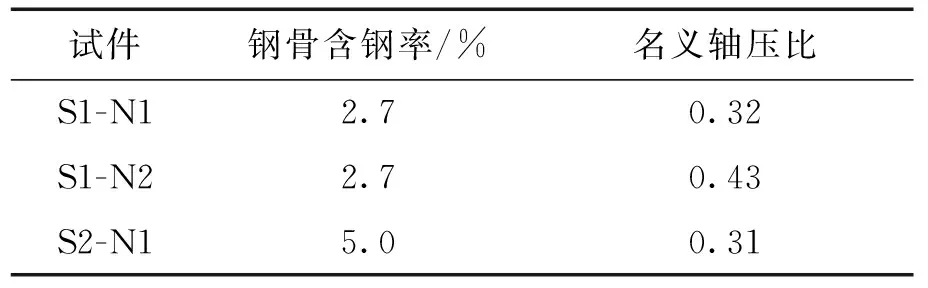
表1 荷載試驗(yàn)參數(shù)Tab.1 Experimental variables of load test specimens

2 長(zhǎng)期變形的計(jì)算

混凝土結(jié)構(gòu)的長(zhǎng)期變形計(jì)算主要包括兩個(gè)方面的內(nèi)容:1) 關(guān)于混凝土的收縮和徐變模型的選擇;2) 采用什么分析方法在混凝土結(jié)構(gòu)中考慮收縮和徐變的影響．

2.1 徐變和收縮預(yù)測(cè)模型

關(guān)于混凝土的徐變和收縮的預(yù)測(cè),已有多種模型提出．其中ACI 209(1992)模型和CEB-FIP90模型是最常用的2種預(yù)測(cè)模型[6-7]．對(duì)這2種模型的預(yù)測(cè)效果,Gardner等[8]利用RILEM數(shù)據(jù)庫(kù)進(jìn)行了評(píng)估,該數(shù)據(jù)庫(kù)匯集了來(lái)自世界各地的徐變與收縮的試驗(yàn)數(shù)據(jù)．他們的研究表明,ACI 209模型對(duì)于徐變的預(yù)測(cè)不太理想,與試驗(yàn)數(shù)據(jù)相比,低估了徐變值;而CEB-FIP90模型則對(duì)于收縮的預(yù)測(cè)不理想,因?yàn)槠滹@著低估了收縮值．基于這個(gè)研究結(jié)果,本文對(duì)于徐變的預(yù)測(cè)選用了CEB-FIP90模型,而對(duì)于收縮的預(yù)測(cè)則選用了ACI209模型．

在選用ACI 209(1992)模型對(duì)本文試驗(yàn)中所用的混凝土收縮值進(jìn)行預(yù)測(cè)時(shí),所用的參數(shù)如下:相對(duì)濕度為60%,體表面積比(V/S)為160 mm,塌落度為50 mm,細(xì)骨料與整體骨料用量比值為34%,水泥質(zhì)量濃度為512 kg/m3,含氣量2%,早期潮濕養(yǎng)護(hù)1 d．

在選用CEB-FIP90模型對(duì)本文試驗(yàn)中所用的混凝土徐變值進(jìn)行預(yù)測(cè)時(shí),所用的參數(shù)如下:斷面面積為25 600 mm2,斷面與大氣接觸的周長(zhǎng)為640 mm,相對(duì)濕度為60%,齡期28 d的混凝土平均抗壓強(qiáng)度為32.5 MPa(這里采用的是150 mm×300 mm圓柱體抗壓強(qiáng)度,是由實(shí)測(cè)的150 mm立方體抗壓強(qiáng)度乘以一個(gè)轉(zhuǎn)換系數(shù)0.83得到[9]),加荷齡期為28 d．

2.2 柱的長(zhǎng)期變形分析方法

齡期調(diào)整有效模量法是在混凝土結(jié)構(gòu)中計(jì)算由于徐變和收縮導(dǎo)致的應(yīng)力和變形時(shí)最常用的數(shù)值分析方法之一[10]．根據(jù)齡期調(diào)整有效模量法,在時(shí)刻t時(shí),混凝土總的應(yīng)變值可以表示為在加載時(shí)刻τ0施加的初始應(yīng)力σ0所產(chǎn)生的瞬時(shí)應(yīng)變和徐變,由t時(shí)刻的應(yīng)力增量Δσ(t)產(chǎn)生的瞬時(shí)應(yīng)變、徐變和收縮應(yīng)變的和,即:

(1)

式中:Ec(τ0)是τ0時(shí)刻混凝土的彈性模量,φ(t,τ0)是徐變系數(shù),εsh(t)是收縮應(yīng)變,χ(t,τ0)為老化系數(shù),用于計(jì)算當(dāng)應(yīng)力是逐漸增加時(shí)的徐變．

式(1)中,徐變系數(shù)φ(t,τ0)和收縮應(yīng)變?chǔ)舠h(t)可以從2.1節(jié)中介紹的預(yù)測(cè)模型得到,老化系數(shù)χ(t,τ0)選用文獻(xiàn)[11]給出的經(jīng)驗(yàn)表達(dá)式:

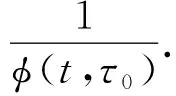
(2)

對(duì)于本次長(zhǎng)期荷載試驗(yàn)的鋼骨混凝土短柱,柱子承受恒定的軸向壓力．假定鋼材為線彈性,利用式(1)所描述的混凝土本構(gòu)方程,再結(jié)合柱子在任何時(shí)刻應(yīng)該滿足的內(nèi)外力平衡方程以及截面的變形協(xié)調(diào)方程,可以求得由于混凝土的收縮和徐變導(dǎo)致的柱隨時(shí)間發(fā)展的變形．具體的分析過(guò)程和步驟可以參見(jiàn)文獻(xiàn)[12]．

2.3 分析結(jié)果與試驗(yàn)曲線的比較

按上述方法求得柱子隨時(shí)間發(fā)展的變形曲線,與實(shí)測(cè)曲線進(jìn)行比較,如圖2所示．對(duì)試件S2-N1和 S1-N1,分析結(jié)果與實(shí)測(cè)結(jié)果吻合良好．但對(duì)試件S1-N2,分析結(jié)果低估了實(shí)測(cè)的長(zhǎng)期變形值．其原因可能在于,試件S1-N2的長(zhǎng)期荷載軸壓比較高,柱中的混凝土發(fā)生了非線性徐變,而這部分非線性徐變的效應(yīng),在分析時(shí)沒(méi)有考慮．

3 結(jié) 論

本文開(kāi)展了鋼骨混凝土短柱在長(zhǎng)期軸向荷載作用下變形發(fā)展的試驗(yàn)研究,并采用齡期調(diào)整有效模量法進(jìn)行了分析計(jì)算,得到以下結(jié)論:

在長(zhǎng)期荷載作用下柱試件的變形增長(zhǎng)較為顯著．試件S2-N1,S1-N1 和 S1-N2在加載202 d時(shí)最終的應(yīng)變值分別達(dá)到了初始彈性應(yīng)變值的1.93,2.22和2.73倍．長(zhǎng)期變形值隨鋼骨含鋼率的增加有所降低,但隨軸壓比的增加而相應(yīng)增大．

采用ACI 209的收縮模型和CEB-FIP90的徐變模型,利用齡期調(diào)整有效模量法可以較好地模擬鋼骨混凝土柱在長(zhǎng)期軸向荷載作用下的變形發(fā)展．但對(duì)于長(zhǎng)期荷載軸壓比較高的柱,該方法會(huì)低估其長(zhǎng)期變形值．

[1] El-Tawil S，Deierlein G G.Strength and ductility of concrete encased composite columns[J].Journal of Structural Engineering，1999，125(9)：1009-1019.

[2] Young B，Ellobody E.Performance of axially restrained concrete encased steel composite columns at elevated temperatures[J].Engineering Structures，2011，33：245-254.

[3] Denavit M D，Hajjar J F，Leon R T.Stability analysis and design of steel-concrete composite columns[C]∥Proceedings of the Annual Stability Conference.Grapevine,United States：Structural Stability Research Council，2012：98-116.

[4] Shanmugam N E,Lakshmi B.State of the art report on steel-concrete composite columns[J].Journal of Constructional Steel Research，2001，57(10)：1041-1080.

[5] Gilbert R I.Time effects in concrete structures[J].Developments in Civil Engineering，1988，23:361-365.

[6] Rhodes J A，Carreira D J.Prediction of creep,shrinkage,and temperature effects in concrete structures[M].Hills,United States:American Concrete Institute，1982.

[7] Comite Euro-International du Beton.CEB-FIP model code 1990:design code[M].London：Thomas Telford，1993.

[8] Gardner N J，Lockman M J.Design provisions for drying shrinkage and creep and normal-strength concrete[J].ACI Mater.Journal，2001，98(2)：159-167.

[9] 沈蒲生.混凝土結(jié)構(gòu)設(shè)計(jì)原理[M].北京：高等教育出版社，2005：17-18.

[10] Bazant Z P.Prediction of concrete creep effects using age adjusted effective modulus method[J].ACI Journal，1972，69(4)：212-217.

[11] 孫寶俊.混凝土徐變理論的有效模量法[J].土木工程學(xué)報(bào)，1993，15(3)：66-88.

[12] Chen Z Y，Wang Y，Chen W.Deformation and stress redistribution of SRC columns under long-term axial compression[C]∥Proceedings of the 2011 International Symposium on Innovation & Sustainability of Structures in Civil Engineering.Xiamen，China:[s.n.]，2011:300-307.