“主題詞教學法”在高等數學課程中的運用

努恩吉雅,寶英華,張曉軍

(河套學院 理學系，內蒙古 巴彥淖爾市 015000)

一、引言

《高等數學》是理工科與部分文科專業的一門重要的基礎課。高等數學課程的教學質量直接影響學生專業課的接受程度，從而影響學生素質的培養與能力的提高。通過高等數學的學習，逐步培養學生具有抽象概括問題的能力、邏輯推理能力、空間想像能力、自學能力、熟練的運算能力、綜合運用所學知識去分析問題和解決問題的能力。因此，高等數學教育工作者不斷嘗試與探索新的教學方法是社會發展的必然。

“主題詞教學法”是一種新的教學方法。在實際的教學過程中，老師先把本節課的主題詞展示在學生面前，每節課的“主題詞”包括本節課的理論知識、蘊含的思想方法和思維方式、做題技巧、課程美與方法美、提升綜合素養與綜合能力等方面的內容構成，其中每個主題詞間用分號隔開。主題詞教學法以“主題詞”為主要線索，對本節課的學習內容展開探究與討論，實現知識與技能、能力與情感態度的培養目標。

二、案例

以同濟大學《高等數學》“直角坐標系下二重積分的計算”的課堂教學過程實施為例，來說明“主題詞”教學法的運用。

(一)體現主題詞

講授新課之前老師利用多媒體課件或在黑板的頂上方寫入本節課的主題詞：①單積分；二重積分；積分區域；X—型區域；Y—型區域；②類比；觀察與聯想；分類；推廣；轉化與化歸；數形結合；③對稱美；符號美；統一美。其中主題詞①主要體現了本節課的重要知識點與理論基礎，通過這些主題詞，學生對本節課的知識內容有了初步印象；主題詞②體現了本節課中所用到的數學思想與方法，通過這部分主題詞，能實現教學中學生的能力目標的提高；主題詞③體現了本節課中隱含的數學之美，能實現教學中培養學生的情感態度與價值觀的提高。

(二)依主題詞展開課堂教學

1.首先復習回顧二重積分的概念以及幾何應用(對應主題詞：二重積分；積分區域；觀察與聯想；分類)。

通過對上節課的二重積分概念與幾何意義的復習，讓學生觀察和聯想，引導啟發學生探索在不同的積分區域中曲頂柱體的體積的求法，從而引出X—型區域、Y—型區域的分類求解法。

2.X—型區域中二重積分的計算方法(對應主題詞：積分區域；X—型區域；轉化與化歸；數形結合；符號美)。

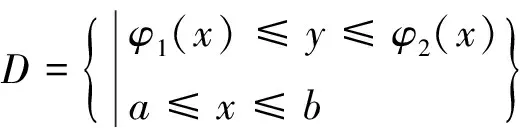
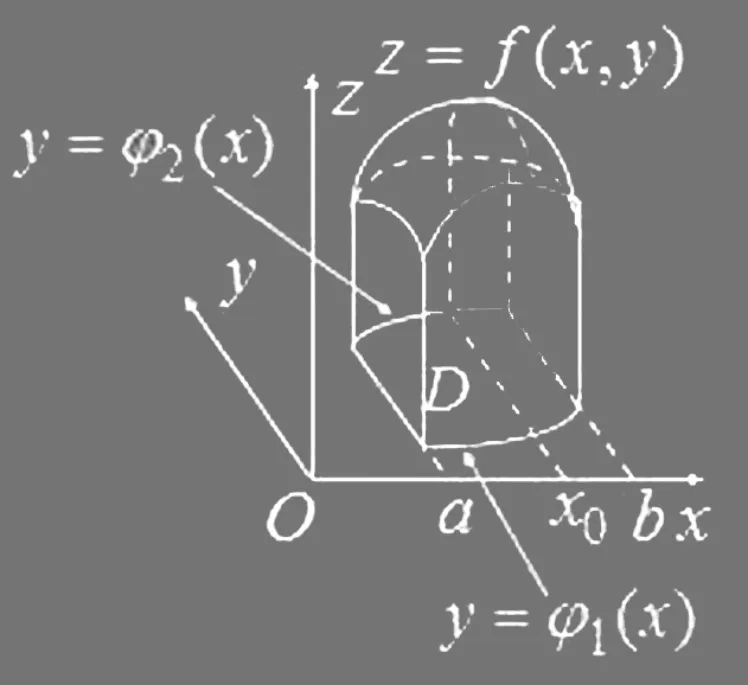
圖1

圖2

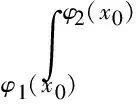
故曲頂柱體體積為

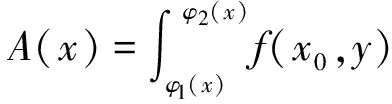
即可得：

此處，提示學生在推導過程利用了轉化與化歸的思想，即把二重積分化為累次的二次積分(定積分)來計算。

3.Y—型區域中二重積分的計算方法(對應主題詞：Y—型區域；類比；推廣；統一美；對稱美)。

同理，曲頂柱體的底為圖3所示，

D={(x,y)|Ψ1(y)≤x≤Ψ2(y),c≤y≤d}

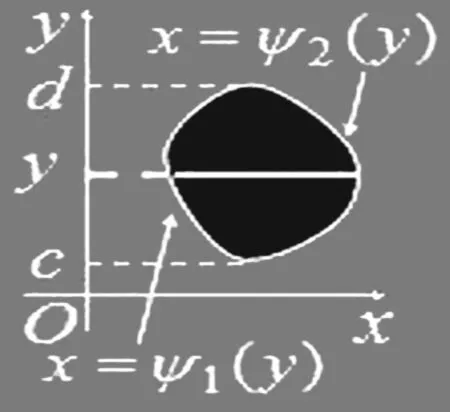
圖3

則其體積可按如下兩次積分計算

4.對比X—型區域、Y—型區域中二重積分的計算公式，強調兩種區域的特點，引導學生做題時正確選擇方法。

5.把二重積分正確的轉化為累次積分，并且確定累次積分的上、下限，把二重積分作為二次積分來處理。選擇積分次序時應以盡量降低積分難度為原則，既考慮積分區域還要分析被積函數。

三、“主題詞”教學法在教學中主要作用分析

(一)“主題詞”教學法有助于教師科學的備課

教師運用主題詞教學法進行教學時，對每堂課、每個章節備課時，都有意識地去挖掘“主題詞”，同時就本節課的“重點”“難點”“要達到目的”“有什么要求”“蘊含什么方法”“內在美”等問題進行思考，所以備課時目的性十分明確。數學是解決實際問題的，所以每節課備課時老師都要帶著問題去看課本；數學是目標明確的，每個數學概念和方法都有其目的。教師要依據目的來合理處理教材，采取恰當的教學方法。這樣才能使學生在學習數學的過程中，提高思維能力，培養發現和提出問題的能力，以及分析和解決問題的能力。只有這樣，才能真正發揮數學的內在力量，實現“數學育人”。

(二)“主題詞”教學法有助于老師對教學內容系統把握

如果教師對教學內容不是熟悉，那么絕對提煉不出正確的“主題詞”。所以，主題詞教學法首先要求教師對教學內容十分準確的理解與把握。教師向學生傳授的知識、思想方法及對內容的體驗，必須自己把握的十分準確，不能似是而非。對于數學尤其是這樣，數學概念是不能含糊的，數學語言應該是很精練準確的，即使是最簡單的概念問題，也要準確把握。主題詞教學法要求教師對教材深入鉆研，包括熟悉全冊教材，熟悉教學大綱，掌握教材的知識體系，深刻理解每一篇章，每節課的內容，明確它在全書的地位和前后的聯系等。教師要深刻準確地把握教材，必須查閱資料，認真鉆研，使教材由“薄”到“厚”。

(三)“主題詞”教學法有助于教師對學生的了解

運用主題詞教學法進行教學的過程中我們制作了與學生互動的“課程學習檔案”[4]，學生上完每節課都要填寫“聽課后需要解決的疑問”“作業中需要解決的疑問”“新發現的解題方法，習題新解法”“分析自己的收獲、不足、努力方向”等內容，每周收一次。通過每周的“課程學習檔案”，老師可以及時發現學生對本周哪些內容有疑惑，哪些問題需要解答。

參考文獻：

[1]張曉軍，楊樹生.“主題詞”教學法[J].新天地:高校論壇,2011(12)：8.

[2]成樂,張曉軍,楊樹生.“主題詞教學法”在課堂教學中運用的效果分析[J].赤峰學院學報，2014(2).

[3]同濟大學數學系.高等數學[M].北京:高等教育出版社，2013.

[4]張永勝.多元學與教方式有效融入日常教學[M].呼和浩特:內蒙古人民出版社，2010.