數控加工中心任務與刀具集成調度模型及改進自適應遺傳算法

周光輝,苗發祥,李彥廣

(1.西安交通大學機械工程學院, 710049, 西安;2.西安交通大學機械制造系統工程國家重點實驗室, 710049, 西安)

數控加工中心任務與刀具集成調度模型及改進自適應遺傳算法

周光輝1,2,苗發祥1,李彥廣1

(1.西安交通大學機械工程學院, 710049, 西安;2.西安交通大學機械制造系統工程國家重點實驗室, 710049, 西安)

為解決數控加工中心任務與刀具的集成優化調度問題,以生產總成本最小為優化目標,建立了考慮任務交貨期和工步并行加工的數控加工中心任務與刀具集成調度模型,產生面向數控加工中心任務與刀具的協同優化調度結果。為實現對該調度模型的優化求解,提出了一種改進自適應遺傳算法,設計了合理的編碼方式和自適應進化操作,并通過任務-刀具關聯矩陣保證搜索過程中解的可行性,從而顯著提高了算法的收斂性能和求解效率。算例結果表明,該模型能夠最大限度地降低加工成本和拖期率,同時算法的收斂速度和穩定性也得到了明顯提高,大大降低了問題求解的迭代次數。

數控加工中心;刀具調度;并行加工;自適應遺傳算法

隨著車間加工自動化程度的日益提高,數控裝備逐漸取代傳統的加工機床,成為企業加工的核心,顯著提高了企業的加工質量與效率,而刀具作為數控加工中心的重要組成部分,受到了越來越多的關注[1]。與傳統的加工機床相比,數控裝備特別是高端數控加工中心(如車銑復合加工中心)更能適應多品種、小批量生產模式需求,具有多工序、多工步并行加工的特點,能滿足復雜多尺度產品的加工需求[2]。但是,在數控加工中心的加工過程中,為保證其多任務的柔性、高效、高質量、低成本加工需求,加工任務(工序、工步)的合理排序與刀具資源的合理選配已經成為迫切需要解決的關鍵問題,二者相輔相成、缺一不可。特別是刀具資源在逐步成為企業瓶頸資源的基礎上,刀具選配的合理與否將直接關系到任務的加工效率和生產成本。在此環境下,探求一種合適的任務與刀具集成調度方案對提升數控加工中心的加工質量與效率就顯得尤為重要[3-6]。

在傳統的數控加工中心加工中,任務與刀具規劃調度是割裂開來的[7-8]。加工任務的規劃與調度過程中未考慮刀具的制約因素,并假定刀具資源是充足的,而刀具的選配則是依據規劃好的加工任務(加工順序)來直接分配,二者是一種串行的因果關系。顯然,該方法并未充分考慮任務與刀具之間的制約關系,從加工成本、加工效率等角度考慮,得出的方案往往是可行方案,而非最佳方案,甚至導致不可行方案的產生。為此,本文針對單臺數控加工中心,從任務與刀具調度協同優化的角度出發,提出一種數控加工中心任務與刀具集成調度方法與模型,并采用自適應遺傳算法實現對模型的優化求解,得出任務與刀具優化分配、調度結果,達到提升數控加工中心的加工效率、刀具資源利用率及降低加工成本的目標。

1 數控加工中心任務與刀具集成調度模型

1.1 變量符號定義

在建立數控加工中心任務與刀具集成調度數學模型之前,首先定義如下變量符號。

n:工件數。

Ji:工件i。

ki:工件i的工步數。

m:備選刀具數。

Mt:備選刀具編號。

Xij:工件i的工步j可使用的刀具集合。

Tijt:工件i的工步j用第t把刀具的加工時間。

Ct:刀具t單位時間的使用費用。

yijt:刀具使用系數,工件i的工步j使用刀具t時為1,否則為0。

Di:工件i的理想交貨期。

ui:工件i拖期完工懲罰因子。

B:可并行加工工步組集合。

Sij:工件i的工步j的開始加工時間。

Eij:工件i的工步j的結束加工時間。

Ei:工件i的完工時間。

Ws:整個調度方案的刀具使用費用。

Wf:整個調度方案的任務拖期懲罰費用。

Wtotal:整個調度方案的加工費用指標。

1.2 任務與刀具集成調度數學模型

一臺數控加工中心分配了n個工件{J1,J2,…,Jn}各工序(含1道或多道工步)加工任務,各工序包含的工步加工順序由工藝要求預先確定,某些工步根據實際需要可并行加工。每道工步的可選加工刀具由工藝規程確定(對于特定加工特征,一般存在同類型的多把刀具可以滿足要求),至少有一把待選刀具可對其進行加工,其加工時間隨所選刀具的不同而不同,加工整批任務共有m把待選刀具{M1,M2,…,Mm}可供選擇,n個待加工工件有各自的交貨期要求{D1,D2,…,Dn}。調度的目標是確定所有工件的加工順序并為每道工步選擇合適的刀具,以使整批任務的加工費用指標達到最優。圖1和表1描述了數控加工中心2工件、5刀具的集成調度問題。

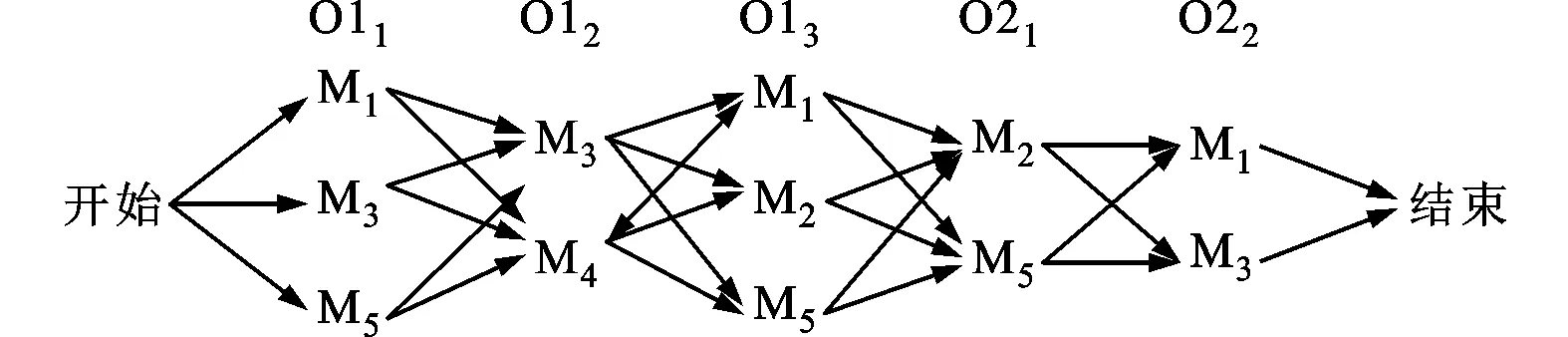
圖1 問題描述示意圖

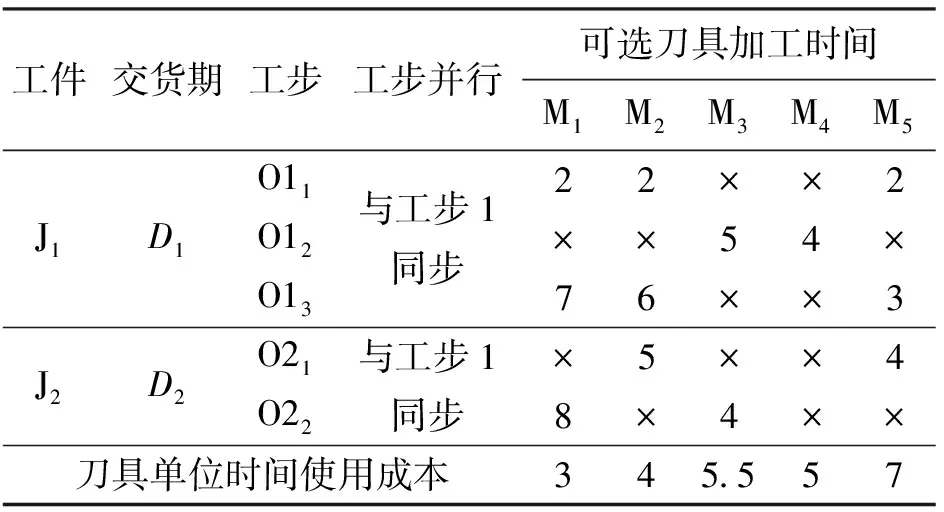
表1 問題加工信息表

注:“×”表示分配在該加工中心上的對應工步不可用該刀具進行加工;O11表示工件1的第1道工步,其余依次類推。

加工過程中需要滿足以下約束條件。

(1)不同工件的工步之間沒有先后約束,同一工件的工步之間有先后關系,且提前已知,不可改動。

(2)同一工件的不同工步之間存在并行加工關系,并行加工情況提前已知。

(3)每個工件一旦開始加工不能中斷。

(4)同一把刀具在某一時刻只能加工一個零件。

(5)工件具有各自的理想交貨期和極限交貨期。

(6)所有工件在零時刻都可以被加工。

基于以上假設,本文以最小化加工費用為優化目標,除刀具使用費用外,由于考慮交貨期要求,可能會存在工件不能準時完工的情況,所以如何減小拖期工件數量,降低拖期懲罰費用也是本問題的關鍵。綜上,總費用應包括刀具使用費用和拖期懲罰費用,由問題定義易知刀具使用費用為

(1)

零件拖期懲罰費用(此處假設這部分費用是滯后時間的線性函數)為

(2)

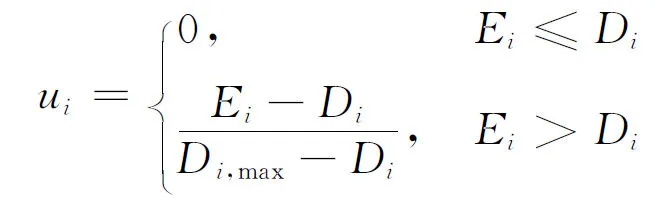
(3)

式中:Di,max為任務的極限交貨期,與理想交貨期Di的差值說明了工件的重要性。越重要的工件其交貨期控制越嚴格,所允許的變動量就越小,反之越大。

據此得到加工費用指標的目標函數為

(4)

并受如下約束

(5)

(6)

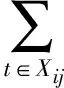
(7)

Num{X11,…,X1k1,…,Xij,…,Xnkn}≤m

i=1,2,…,n;j=1,2,…,ki

(8)

Eij=Sij+Tijt,

i=1,2,…,n;j=1,2,…,ki;t∈Xij

(9)

Eij≤Si(j+1),i=1,2,…,n;j=1,2,…,ki

(10)

Ei≤S(i+1)j,i=1,2,…,n

(11)

Sij1=Sij2, [(i,j1),(i,j2)]∈B

(12)

式(5)說明,由于考慮了并行加工,可以有多把刀具同時進行加工;式(6)保證每把刀具同時只能加工一道任務;式(7)保證調度為所有任務的全排列;式(8)表示用于零件加工的所有刀具數量Num{·}不大于所提供的備選刀具數量;式(9)表示完工時間等于開始時間與加工時間之和;式(10)、式(11)保證后一道加工任務必須在前一道加工任務完成后開始;式(12)則保證并行加工的工步同時開始。

2 自適應遺傳算法的設計

由于傳統遺傳算法在求解類似問題過程中,存在著收斂速度慢,常陷于局部最優值的缺點。本文為實現對刀具與任務集成調度問題的綜合求解,采用自適應遺傳算法,通過在搜索過程中,交叉、變異概率的自動變化來提高算法的收斂速度,跳出局部最優解。算法流程如圖2所示。

圖2 自適應算法流程圖

2.1 染色體編碼與解碼

數控加工中心的刀具與任務集成調度問題需要為每個工件的每道工步選擇一把刀具,并對所有待加工任務進行排序,因此編碼需同時考慮這兩方面的問題。總體上采用如下實數矩陣編碼結構

為同時解決刀具選配和工件排序的問題,編碼由兩部分組成,aij是由整數部分和小數部分組成的實數。aij的整數部分是刀具染色體,表示工件i的第j道工步選擇第[aij]把刀具進行加工([·]表示取整數),若[aij]=[aik], 且j≠k,則表示同一工件的不同工步采用相同刀具進行加工;aij的小數部分是加工順序染色體,定義工件的加工順序指標為

{·}表示取小數。約定按Pi值由小到大確定各工件的加工順序。融合這兩部分編碼,便可形成一個表示刀具與任務集成調度方案的矩陣編碼。

為保證整個矩陣的維數相同,約定凡小于最大工步數的工件整數部分編碼用0表示。例如圖1的工件2、刀具5調度問題,其矩陣編碼為

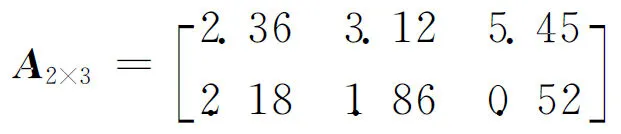
通過對矩陣元素的拆分后,即可確定調度方案,即先加工工件2,再加工工件1;工件2的2道工步分別采用刀具2和刀具1進行加工;工件1的3道工步分別采用刀具2、3、5進行加工。

2.2 適應度函數

適應度值是評價解的優良性能的重要指標,本文是求解目標函數最小化問題,故采用如下反比例函數作為適應度函數

(13)

式中:Wlk是第k代種群中第l個染色體的目標函數值;W*是第k代種群中最小的目標函數值;a是平均目標函數值與最小目標函數值之間的距離。

2.3 初始解的生成

初始解的質量對于遺傳算法的求解效果有較大影響,采用隨機初始化會產生較多的不可行解,需要算法在優化過程中不斷剔除,這就增加了搜索過程的迭代次數和收斂時間。本文通過引入工步-刀具關聯矩陣來保證進化過程中刀具分配方案的可行性。若用yijt表示矩陣元素(i為工件號,j為工步號,t為刀具號),其取值規則為

對于圖1,其工步-刀具關聯矩陣見表2。

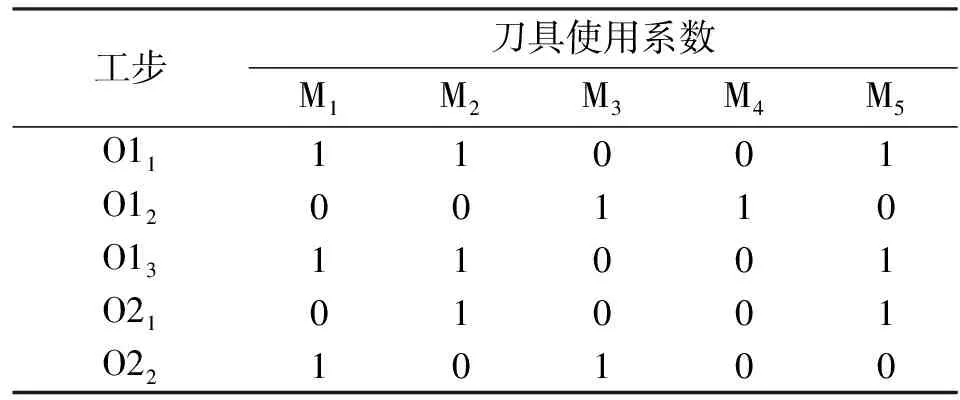
表2 工步刀具關聯表

在解編碼的初始化與交叉、變異過程中,始終對照該矩陣,選擇yijt=1的刀具號生成編碼,從而產生可行調度方案,提高算法搜索過程的穩定性。

2.4 算法的進化操作

交叉操作主要為保留父代個體的優秀基因。為保證交叉之后染色體的合法性,本文采用染色體同位置基因互換的方法,基于該原則,交叉操作可以多樣化設計。本文針對矩陣編碼分別采用基于行和列的單點、兩點和多點交叉,如圖3、圖4所示。

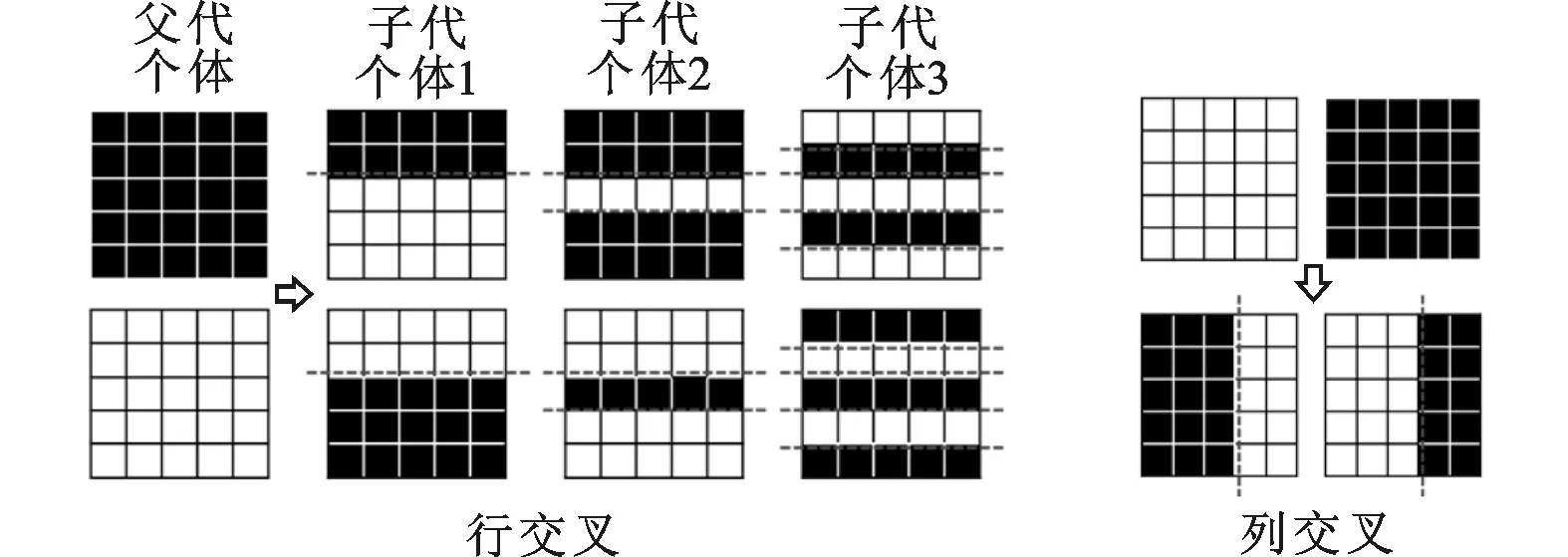
圖3 改進自適應遺傳算法交叉操作

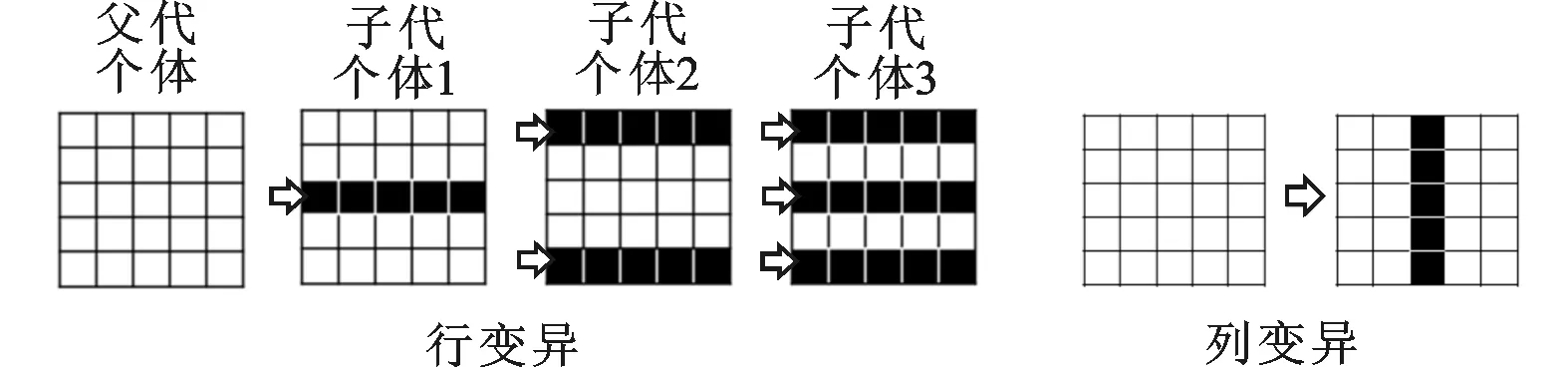
圖4 改進自適應遺傳算法變異操作

類似交叉操作,變異也采用基于行和列的單點、兩點和多點變異。在變異過程中,要保證[aij]∈Xij,從而保證染色體的合法性。

對于交叉、變異過程,優良個體以較高的概率交叉更符合自然法則;低劣個體以較大概率變異,這更有利于保護并產生新的優良解。這一原則應該體現在整個進化操作過程中。文獻[9]對自適應遺傳算法的Pc、Pm做以下調整

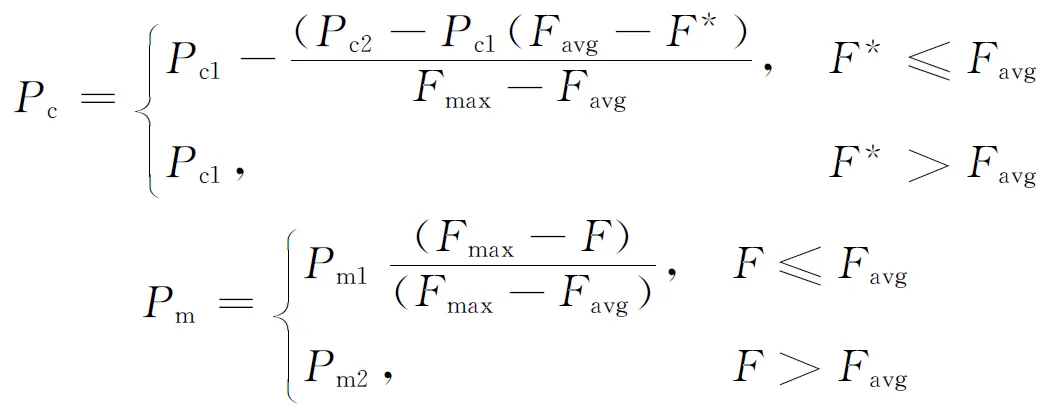
式中:Fmax為種群的最大適應度值;Fmin為最小適應度值;Favg為平均適應度值;F*為交叉個體中較小的適用度值;F為變異個體的適應度值。

上述調整一定程度上改進了遺傳性能,但不足之處在于,用線性函數表示交叉、變異概率的變化過程,無法描述整個進化過程中參數的變化幅度。為了更清晰地說明在進化不同階段參數變化的幅度區別,進一步提高算法的自適應性,本文引入三角函數來表示這一變化過程,重新給出交叉、變異概率的計算公式如下

(14)

(15)

如圖5所示,在交叉操作中,當F*=Fmax時,Pc=Pc2,適應度最小的個體以最大的交叉概率將基因遺傳至下一代。在變異操作中,當F=Fmax時,最優個體得到保護直接進入下一代,而當F=Fmin時,Pm=Pm2,最差的個體以最大的概率進行變異,以生成較為優良的個體。圖5曲線的斜率可以清楚說明整個進化過程中各參數的變化趨勢。同時,為保證每一代的優良個體不被破壞,本文采用精英選擇策略,對前10%的優秀個體進行保護,確保算法的全局尋優性。

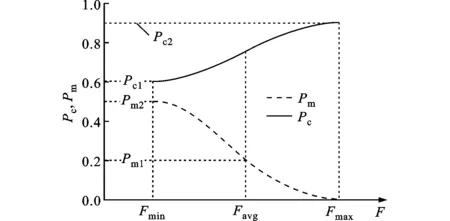
圖5 遺傳算法交叉、變異概率自適應變化曲線

3 實例驗證與結果分析

為了驗證模型的正確性,并比較本文自適應遺傳算法在解決該問題中的優越性,特設計加工實例進行分析。在模型方面,設計按交貨期順序加工模型與本模型進行對比;在算法上,設計傳統遺傳算法與本算法進行比較。

3.1 加工實例介紹

本文以西安西電開關有限公司機加車間為應用示范基地,以型號NH6300-DCG的數控加工中心的一批實例加工任務為例,計算其調度過程。實例中,該加工中心分配了10個工件某一道工序的加工任務,每道工序包含了多道工步。現提供12把待選刀具對整批任務進行加工,與任務相關的刀具需求信息、加工時間、刀具使用成本、并行加工信息及各加工任務交貨期等信息如表3、表4所示。

表3 任務加工信息表

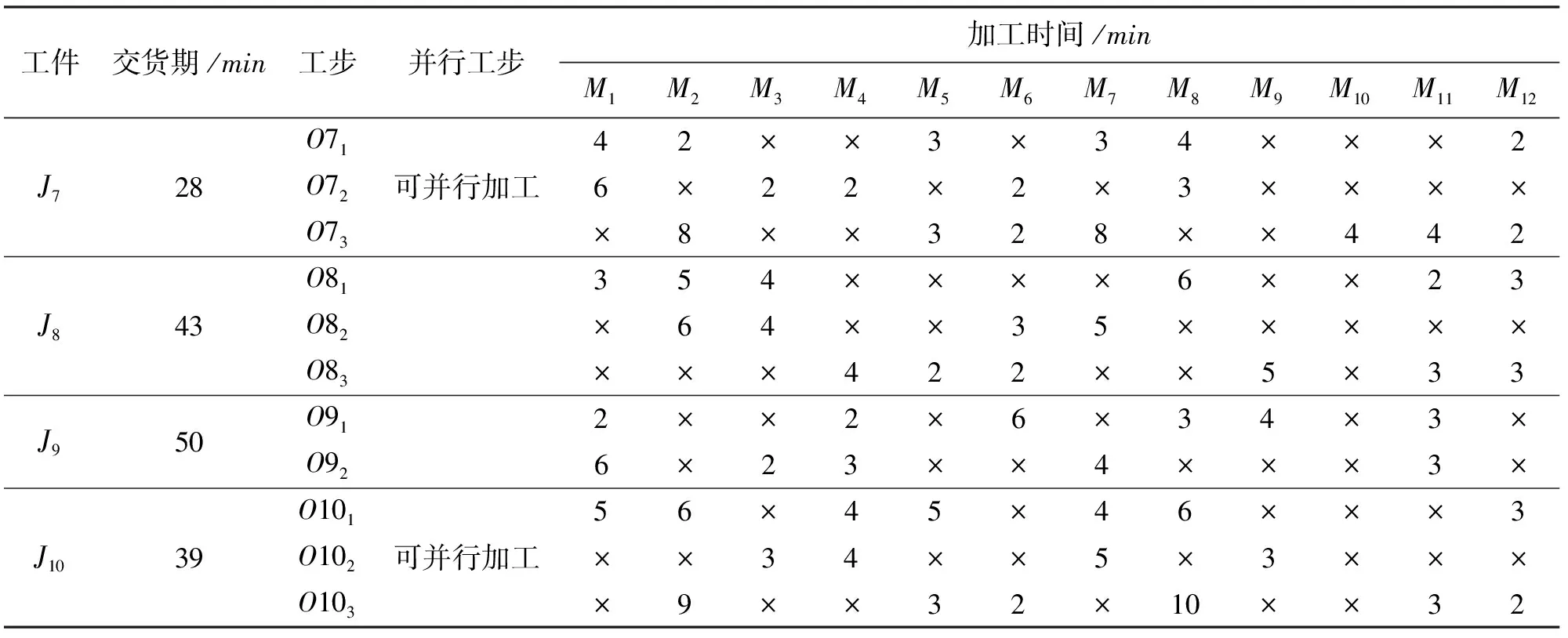
續表

表4 刀具使用成本表

改進自適應遺傳算法采用MATLAB編程實現,最小、最大交叉概率Pc1=0.6、Pc2=0.9,最小、最大遺傳概率Pm1=0.2、Pm2=0.5,種群規模設置為100,迭代次數為300次。

3.2 結果對比與分析

調度結果如圖6所示,圖中方框代表對應Z步加工過程,垂直線Di代表工件i的交貨期。由圖6a可知,在按交貨期排序的加工方案中,從第3個工件開始拖期完工,拖期率達70%,拖期懲罰Wf=276元。在圖6b工序優化后的方案中,只有工件1、2沒有按交貨期要求進行加工,拖期率降到20%,相應的拖期懲罰Wf=94.5元。

表5對兩種方案的調度結果進行了對比,可以看出,采用遺傳算法在對刀具進行選配的同時,對加工序列進行不斷調整,可以最大限度地減少拖期工件數量,降低拖期懲罰,證明了本模型的可行性。

由以上結果可以看出,常規按照交貨期順序進行加工的調度方案會造成延誤時間的疊加,從而影響任務整體的正常生產。采用本模型,通過損失部分不緊急子任務的準時生產,可以最大限度地換取任務整體加工的準時性。同時,本文的調度方案可以用于指導交貨期的制定,如對工件1和工件2的交貨期作適當調整,則整批任務的生產計劃和調度方案則會更加合理。

由圖7、圖8實例求解的收斂過程可知,相比傳統遺傳算法,改進后的自適應遺傳算法在最優值的收斂速度和平均值的穩定性方面都有較明顯的提高,傳統遺傳算法需要250次迭代,而本算法只需要50次迭代,從而大大降低了算法收斂所需的迭代次數。

表5 調度結果對比表

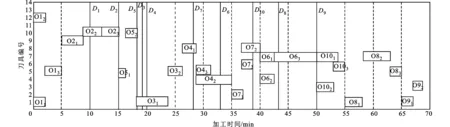
(a)按工件交貨期排序

(b)自適應遺傳算法對工序進行優化

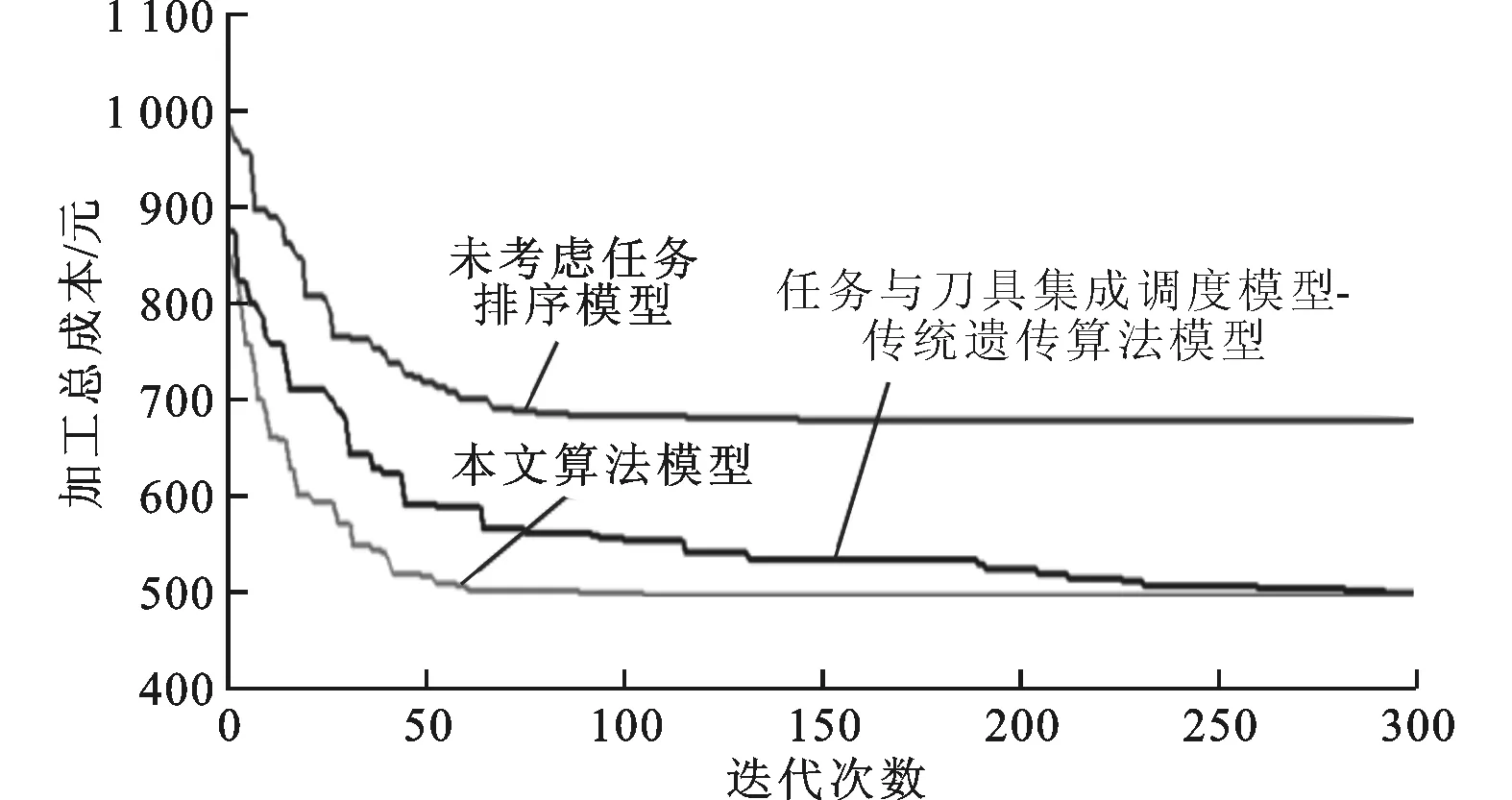
圖7 適應度最優值收斂曲線比較

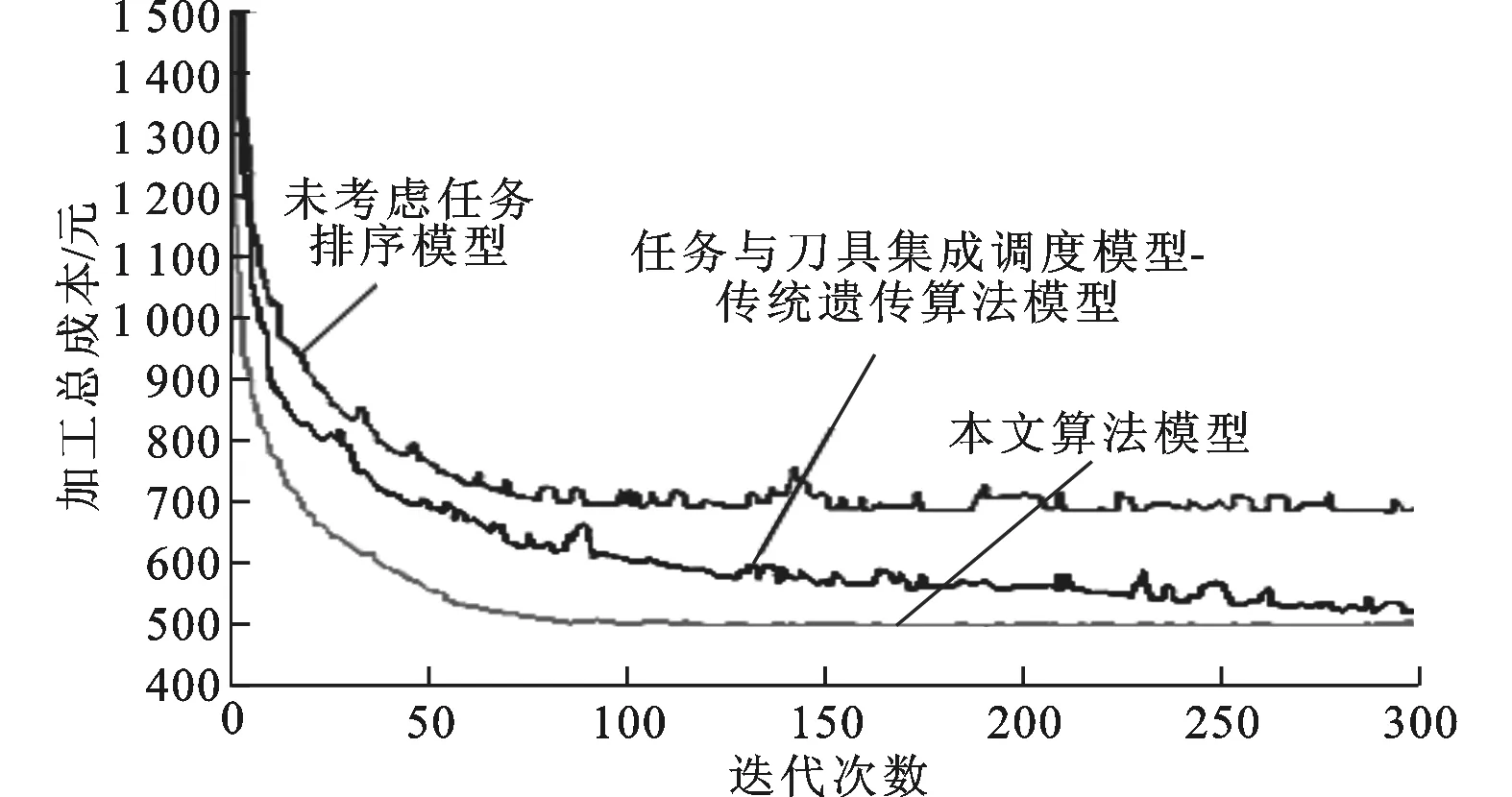
圖8 適應度平均值收斂曲線比較

4 結束語

對于數控加工中心的一批加工任務來講,刀具選配與任務規劃是影響加工總成本的兩個關鍵環節,只有將兩者結合在一起共同優化,才有可能得到該批任務加工總成本的全局最優解。為此,本文提出了數控加工中心任務與刀具的集成調度方法與模型,并利用改進后的自適應遺傳算法對該問題進行求解,最后設計加工實例對問題模型和算法進行分析。結果證明,結合本模型和改進后的自適應遺傳算法,可在實際生產中得到更為滿意的結果。

[1] 王解法, 馮祖仁, 李世敬, 等. 柔性制造系統(FMS)刀具建模調度仿真研究 [J]. 系統仿真學報, 2003, 15(9): 1211-1213. WANG Jiefa, FENG Zuren, LI Shijing, et al. Research on tool assembly model and schedule simulation in FMS [J]. Journal of System Simulation, 2003, 15(9): 1211-1213.

[2] 付春林. 高端車銑復合加工中心的應用 [J]. CAD/CAM與制造信息化, 2008(4): 96-98. FU Chunlin. The application of high-end turning-milling center [J]. Digital Manufacturing Industry, 2008(4): 96-98.

[3] BUYURGAN N, SAYGIN C, KILIC S E. Tool allocation in flexible manufacturing systems with tool alternatives [J]. Robotics and Computer-Integrated Manufacturing, 2004, 20(4): 341-349.

[5] 邊培瑩. PSO算法在FMS刀具可復用調度中的應用與仿真 [J]. 機械設計與制造, 2012(3): 76-78. BIAN Peiying. Application and simulation of PSO in FMS based on tools reusable scheduling [J]. Machinery Design & Manufacture, 2012(3): 76-78.

[6] 張亮, 樓佩煌, 胡武茹, 等. 一種改進型遺傳算法在FMS刀具調度中的應用 [J]. 工業控制計算機, 2009, 22(9): 75-78. ZHANG Liang, LOU Peihuang, HU Wuru, et al. Application of an improved genetic algorithm for tool scheduling in FMS [J]. Industrial Control Computer, 2009, 22(9): 75-78.

[7] PRABAHARAN T, NAKKEERAN P R, JAWAHAR N. Sequencing and scheduling of job and tool in a flexible manufacturing cell [J]. The International Journal of Advanced Manufacturing Technology, 2006, 29: 729-745.

[8] 趙丹, 張家泰, 舒海生, 等. 基于雙重遺傳算法的工件流與刀具流綜合調度優化 [J]. 西南交通大學學報, 2010, 45(6): 926-931. ZHAO Dan, ZHANG Jiatai, SHU Haisheng, et al. Double layer genetic algorithm for integrated scheduling optimization of part and tool flows [J]. Journal of Southwest Jiaotong University, 2010, 45(6): 926-931.

[9] 陳世哲, 劉國棟, 浦欣, 等. 基于優勢遺傳的自適應遺傳算法 [J]. 哈爾濱工業大學學報, 2007, 39(7): 1021-1024. CHEN Shizhe, LIU Guodong, PU Xin, et al. Adaptive genetic algorithm based on superiority inheritance [J]. Journal of Harbin Institute of Technology, 2007, 39(7): 1021-1024.

(編輯 杜秀杰)

JobandToolIntegrativeSchedulingModelinCNCMachiningCenterandImprovedAdaptiveGeneticAlgorithm

ZHOU Guanghui1,2,MIAO Faxiang1,LI Yanguang1

(1. School of Mechanical Engineering, Xi’an Jiaotong University, Xi’an 710049, China;2. State Key Laboratory for Manufacturing Systems Engineering, Xi’an Jiaotong University, Xi’an 710049, China)

To solve the integrated scheduling for job and tools in computer numerical control(CNC) machining center, a model considering delivery time and parallel processing of working steps is presented. And the minimized total cost of production is taken as the objective to achieve the collaborative optimization. An improved adaptive genetic algorithm is proposed where a job-tool relationship matrix is adopted to guarantee the legality of solutions, and a rational chromosome encoding and adaptive genetic operations are designed to accelerate the convergence rate and improve solving efficiency. The experimental examples are comparatively analyzed to verify correctness of the model. The proposed algorithm enables to maximally reduce processing cost and job tardiness rate and to improve the convergence rate and stability with greatly reduced iterations.

CNC machining center; tool schedule; parallel machining; adaptive genetic algorithm

2014-03-14。

周光輝(1972—),男,教授,博士生導師。

國家自然科學基金資助項目(51175414);教育部新世紀優秀人才支持計劃資助項目(NCET-12-0452);國家科技支撐計劃資助項目(2012BAH08F02)。

時間:2014-07-28

10.7652/xjtuxb201412001

TH166

:A

:0253-987X(2014)12-0001-07

網絡出版地址:http:∥www.cnki.net/kcms/detail/61.1069.T.20140728.1037.005.html