單噴嘴蒸汽射流凝結引起的壓力振蕩研究

武心壯,邱斌斌,種道彤,嚴俊杰

(1.國家核電技術公司上海核工程研究設計院, 200233, 上海;2.西安交通大學動力工程多相流國家重點實驗室, 710049, 西安)

單噴嘴蒸汽射流凝結引起的壓力振蕩研究

武心壯1,2,邱斌斌2,種道彤2,嚴俊杰2

(1.國家核電技術公司上海核工程研究設計院, 200233, 上海;2.西安交通大學動力工程多相流國家重點實驗室, 710049, 西安)

為了得到蒸汽在過冷水中浸沒射流凝結引起的壓力振蕩規律,針對不同的過冷水溫度和軸向距離對壓力振蕩特性進行實驗研究。實驗系統主要包括蒸汽發生器、穩壓罐、噴嘴、水箱、儀表、可視化系統和數據采集系統。測量得到了不同軸向位置的壓力振蕩峰值,通過快速傅里葉變換得到了壓力振蕩的主頻,并分析了過冷水溫度和軸向距離對壓力振蕩特性的影響規律。結果表明:壓力振蕩峰值總體上隨溫度升高而增大,但在水溫較高時出現下降趨勢;主頻隨著水溫的降低而增大,但不隨軸向距離的增大而變化。同時,利用前人提出的公式對本實驗條件下的主頻進行了計算,計算值與實驗值具有相同的變化趨勢,且吻合得較好。

壓力振蕩;峰值;主頻

由于蒸汽在過冷水中浸沒射流凝結具有高效的混合與換熱能力,因此與其相關的設備廣泛地用于多種工業場合,如能源行業中應用的汽水混合加熱器、蒸汽-水噴射器[1-2],特別是核工業中輕水反應堆的卸壓系統,例如先進反應堆AP1000中安全殼內換料水箱中的鼓泡器卸壓即采用了蒸汽射流凝結換熱的機理。

目前,國內外學者對蒸汽浸沒射流流場參數的研究主要包括壓力、溫度和速度等,其中壓力振蕩特性是相關工業設備設計中關注的內容。美國學者Simpson在研究亞音速蒸汽浸沒射流的過程中,觀察到了周期性的界面運動,以及氣泡生成、生長、分離的過程,并測得了壓力脈動特性[3]。韓國學者Youn等研究了低蒸汽質量流率下間歇流區域的壓力脈動特性,發現壓力波的產生頻率在10～50 Hz時隨著蒸汽質量流率的增加而增加,但是幾乎不受過冷水溫度的影響[4]。韓國學者Cho等實驗研究了多孔蒸汽射流壓力波動特性,結果表明壓力波動頻率隨著蒸汽質量流率和過冷度的增加而增大,并分析了與氣泡動力學特性的關系[5]。此外,美國學者Eden等、劉光耀、潘冬冬等以及本文作者都先后對蒸汽射流流場中的壓力分布進行了研究和分析[1-2,6-9]。

由于蒸汽浸沒射流凝結引起的壓力振蕩是設備設計應關注的問題,但目前國內外對此相關的研究卻比較匱乏,故本文針對不同的過冷水溫度和軸向距離,對蒸汽浸沒射流凝結引起的壓力振蕩特性進行實驗研究,得到了上述參數對壓力振蕩特性的影響規律,為豐富汽液兩相流理論積累了實驗依據,并為相關的設備設計提供了一定的參考。

1 實驗系統與方法

(a)實驗系統示意圖

圖1所示為蒸汽浸沒射流凝結引起的壓力振蕩實驗研究的系統示意圖和測點布置示意圖。實驗系統主要包括蒸汽發生器、穩壓罐、噴嘴、水箱、三維支架、壓力傳感器、熱電偶、可視化系統和數據采集系統。本實驗中直接測量的參數有飽和蒸汽壓力、水箱中過冷水的溫度,以及不同測點處的壓力振蕩特性。蒸汽參數由噴嘴入口的傳感器測量得到,壓力振蕩特性參數由裝在三維支架上的高頻動態壓力傳感器測量,過冷水溫度由裝在水箱中的熱電偶測量。

(b)測點布置示意圖

本實驗在軸向位置布置了3個測點,以研究不同軸向位置的壓力振蕩特性,表1所示為詳細的測點位置和汽水參數。實驗中當汽水參數達到設定值后,移動三維支架上的壓力探針測量設定軸向位置的壓力振蕩特性,本實驗采用NI采集系統,采樣頻率為5 kHz;高頻動態壓力傳感器響應頻率為4 kHz,量程為-100～100 kPa,滿量程精度為0.25%;K型熱電偶精度為1 ℃。由于實驗研究中存在不可避免的測量誤差和系統誤差,本文使用Moffat方法[10]和文獻[11]中介紹的對快速傅里葉變換不確定度的計算方法來分別分析壓力振蕩幅值和振蕩主頻的不確定度。

表1 實驗條件

注：R和X分別為徑向距離和軸向距離與噴嘴出口直徑的比值。

對于直接測量量的不確定度

(1)

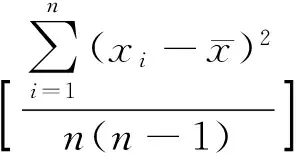
(2)

ub=Δ/31/2

(3)

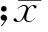
對于快速傅里葉變換引入的不確定度

(4)

urel1=(8m+3)1/2σ

(5)

σ2=2-2B/12

(6)

urel2=ε/81/2

(7)

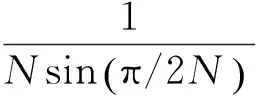
(8)

式中:urel1和urel2分別為疊形運算舍入誤差引入的不確定度分量和窗函數以及柵欄效應引入的不確定度分量;σ2為相對誤差的方差;N為傅里葉變換長度;m=lbN為級數;B為計算機計算長度;ε為窗函數以及柵欄效應引入的最大誤差。根據實驗中使用的壓力傳感器等的精度以及上述不確定度的計算方法,可以得到實驗中壓力振蕩幅值和振蕩主頻的最大不確定度分別為12.6%和12.8%。

2 實驗結果與分析

2.1 幅值

(a)tw=20 ℃

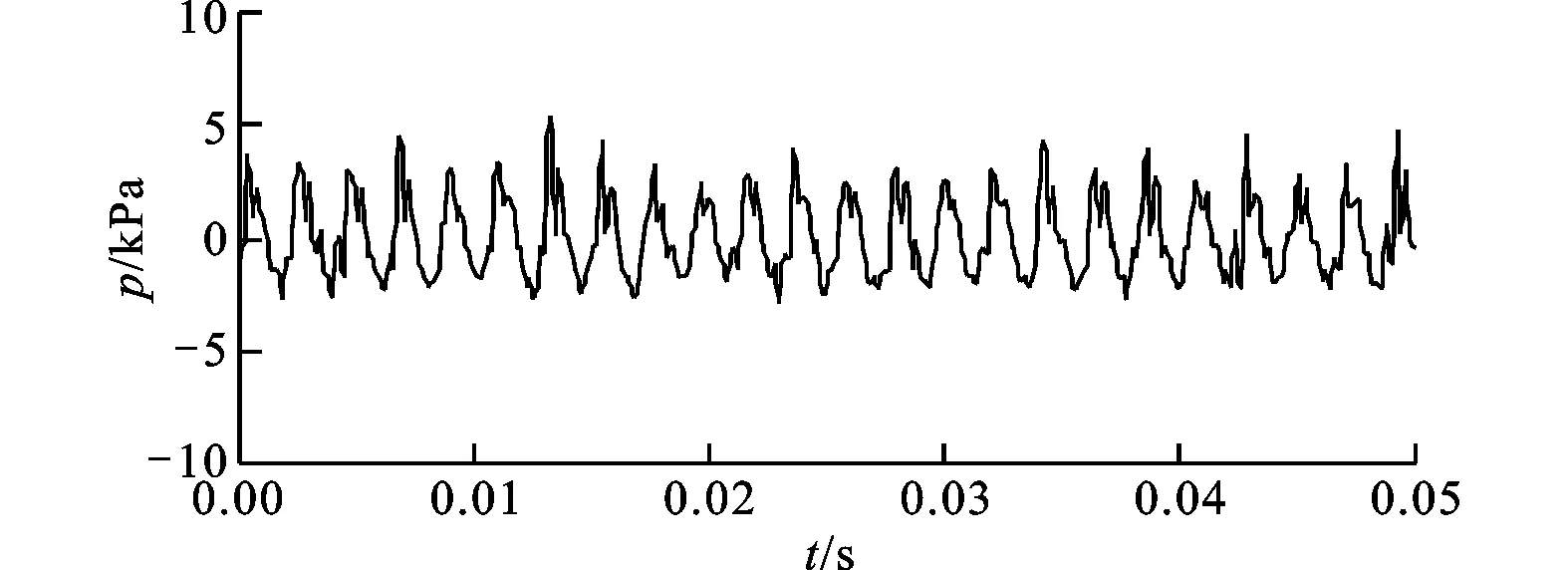
(b)tw=40 ℃

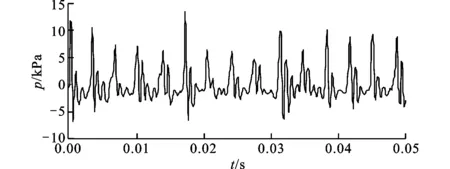
(c)tw=60 ℃

圖2所示為X=0,水溫為20、40和60 ℃時,在時間0.05 s內的壓力振蕩特性。從圖中可以明顯看出壓力振蕩規律,當水溫比較低時,壓力振蕩幅值比較小,隨著水溫的升高,壓力振蕩的幅值逐漸增大。這是由蒸汽凝結特性所決定的,當水溫比較低時,過冷水的冷凝作用強,蒸汽迅速被凝結,汽液界面小且穩定,振蕩幅值小;當水溫升高時,冷凝作用減弱,汽液界面增大并且不穩定,振蕩幅值大。為了便于分析,圖3給出了該蒸汽質量流率下,不同水溫對應的凝結形態。低水溫時,蒸汽射流形成了穩定的汽羽,水溫從40 ℃到50 ℃時,汽羽逐漸不穩定,特別是在高水溫時,汽羽逐漸發散,所以蒸汽射流的壓力振蕩特性與凝結特性和凝結形態是一致的。

圖3 不同水溫下的凝結形態

為了分析壓力振蕩幅值的規律,本文定義壓力振蕩峰值pmax和均方根值p′如下

pmax=max(p1…pN)

(9)

(10)

本文對2 s內的壓力振蕩特性進行分析,圖4所示為不同軸向距離時,壓力振蕩峰值和均方根值隨水溫的變化規律。圖4a中,在本實驗選取的近距離測點內,壓力振蕩峰值在高水溫時可達到20 kPa,當測點較遠時,壓力振蕩峰值約為5 kPa。圖4b反映了壓力振蕩均方根值的變化趨勢。總體上,壓力隨著溫度的升高而升高,但是當水溫達到60 ℃左右時,壓力開始出現下降的趨勢。韓國學者Cho在介紹前人的研究結果時,報告過類似的規律,壓力峰值出現在水溫60～80 ℃左右[5]。本文上述討論中對壓力振蕩幅值隨水溫升高而增大進行了分析,實際上,當在水溫逐漸升高趨于飽和溫度的過程中,冷凝能力逐漸降低,蒸汽射流凝結現象越來越不明顯,從而由凝結產生的壓力振蕩會逐漸消失。因此,隨著水溫上升到一定程度,壓力振蕩幅值出現下降趨勢。

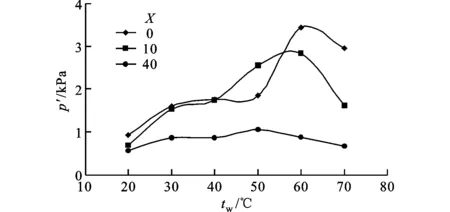
(b)均方根值隨過冷水溫度的變化

2.2 頻率

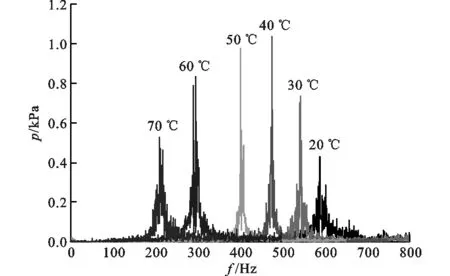
圖5 不同水溫下壓力振蕩的主頻(X=0)

圖2中描述的是蒸汽射流凝結引起的時間域壓力振蕩信號,對于壓力振蕩頻率可以用快速傅里葉變換(FFT)方法分析,并用主頻表征。傅里葉變換把復雜的信號考慮成由一定振幅、相位、頻率的基本正弦(余弦)信號組合而成,將函數向一組正交的正弦、余弦函數展開,傅里葉變換的目的就是找出這些基本正弦(余弦)信號中振幅較大信號對應的頻率,從而找出復雜信號中的主要振動頻率特點,快速傅里葉變換是傅里葉變換的快速算法。圖5所示為X=0時,不同水溫下壓力振蕩的頻域特性。從圖中可以看出,主頻在200～600 Hz之間,且主頻隨著水溫的降低而增大,這也可以直觀地從圖2的時間域壓力振蕩特性中看出。這是由于隨著水溫降低,冷水的過冷度增大,冷凝作用增強,蒸汽迅速被凝結,汽液界面處氣泡存在的時間短暫,所以引起的壓力振蕩頻率大。圖6所示為在水溫為40 ℃時,不同歸一化軸向距離下壓力振蕩的頻域特性。從圖中可以看出,雖然隨著軸向距離的增大,幅值逐漸減小,但是主頻相同。這也說明在壓力振蕩的傳播中,能量逐漸減小,但是頻率不變。

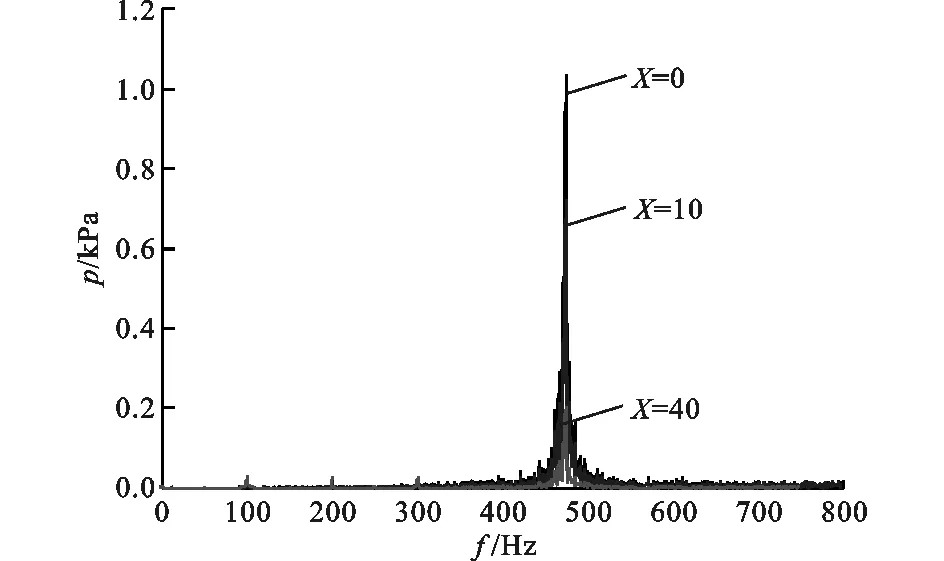
圖6 不同歸一化軸向距離下壓力振蕩的主頻(tw=40 ℃)

Fukuda在對蒸汽凝結引起的壓力振蕩的頻率研究中得到主頻正比于冷水過冷度Δt,反比于噴嘴直徑de,并提出了計算主頻的簡單關系式[12]

f=60Δt/de

(11)

本文利用上述關系式計算得到的頻率與本實驗壓力振蕩FFT分析得到的主頻比較結果如圖7所示,計算值與實驗值的變化趨勢一致,并且吻合得較好,誤差在±8%以內。

圖7 壓力振蕩頻率計算值和實驗值的比較

3 結 論

本文針對不同位置和過冷水溫度,對飽和蒸汽在過冷水中浸沒射流凝結引起的壓力振蕩特性進行了實驗研究,主要結論如下。

(1)蒸汽射流的壓力振蕩特性與凝結特性和凝結形態是一致的。當水溫較低時,壓力振蕩幅值較小,隨著水溫的升高,壓力振蕩的幅值逐漸增大。

(2)壓力振蕩幅值隨著溫度的升高而增大,但是當水溫達到60 ℃左右時,壓力開始出現下降的趨勢。這是由于在水溫逐漸升高趨于飽和溫度的過程中,蒸汽射流凝結現象越來越不明顯,由凝結產生的壓力振蕩會逐漸消失,從而隨著水溫上升到一定程度,壓力振蕩幅值出現下降趨勢。

(3)主頻隨著水溫的降低而增大,這是由于水溫降低時,冷水的過冷度大,蒸汽迅速被凝結,汽液界面處氣泡存在的時間短暫,所以引起的壓力振蕩頻率大。當水溫相同時,主頻不隨軸向距離的增大而變化,這也說明在壓力振蕩的傳播中,能量逐漸減小,但是頻率不變。

(4)利用前人給出的關系式計算得到的頻率與本文得到的主頻變化趨勢一致,并且吻合得較好,誤差在±8%以內。

[1] 武心壯, 潘如東, 嚴俊杰. 蒸汽浸沒射流凝結引起的沖擊特性研究 [J]. 工程熱物理學報, 2012, 33(5): 805-808. WU Xinzhuang, PAN Rudong, YAN Junjie. Research on impact characteristic of steam jet in water [J]. Journal of Engineering Thermophysics, 2012, 33(5): 805-808.

[2] 武心壯, 李文軍, 嚴俊杰. 音速蒸汽浸沒射流凝結軸向全壓分布特性研究 [J]. 核動力工程, 2012, 33(6): 76-80. WU Xinzhuang, LI Wenjun, YAN Junjie. Research on axial total pressure distributions of sonic steam jet in subcooled water [J]. Nuclear Power Engineering, 2012, 33(6): 76-80.

[3] SIMPSON M E, CHAN C K. Hydrodynamics of a subsonic vapor jet in subcooled liquid [J]. ASME Journal of Heat Transfer, 1982, 104(2): 271-278.

[4] YOUN D H, KO K B, LEE Y Y, et al. The direct contact condensation of steam in a pool at low mass flux [J]. Journal of Nuclear and Technology, 2003, 40(10): 881-885.

[5] CHO S, CHUN S Y, BAEK W P, et al. Effect of multiple holes on the performance of sparger during direct contact condensation of steam [J]. Experimental Thermal and Fluid Science, 2004, 28(6): 629-638.

[6] EDEN T J, MILLER T F, JACOBS H R. The centerline pressure and cavity shape of horizontal plane choked vapor jets with low condensation potential [J]. ASME Journal of Heat Transfer, 1998, 120(4): 999-1007.

[7] 劉光耀, 嚴俊杰, 潘冬冬, 等. 超音速蒸汽浸沒射流汽羽形狀及壓力分布的實驗研究 [J]. 工程熱物理學報, 2010, 31(5): 781-784.

LIU Guangyao, YAN Junjie, PAN Dongdong, et al. Research on the steam plume shape and pressure fields of supersonic steam jet in subcooled water [J]. Journal of Engineering Thermophysics, 2010, 31(5): 781-784.

[8] 潘冬冬, 武心壯, 嚴俊杰, 等. 超音速蒸汽浸沒射流尾部速度的實驗研究 [J]. 工程熱物理學報, 2010, 31(8): 1324-1326. PAN Dongdong, WU Xinzhuang, YAN Junjie, et al. Experimental study on velocity distribution for the tail of supersonic steam jet [J]. Journal of Engineering Thermophysics, 2010, 31(8): 1324-1326.

[9] WU X Z, YAN J J, LI W J, et al. Experimental study on a steam-driven turbulent jet in subcooled water [J]. Nuclear Engineering and Design, 2010, 240(10): 3259-3266.

[10]MOFFAT R J. Describing the uncertainties in experimental results [J]. Experimental Thermal and Fluid Science, 1988, 1(1): 3-17.

[11]宋瓊, 朱長春, 牛寶良. 基2快速傅里葉變換引入的不確定度估算 [J]. 計量學報, 2004, 3(25): 281-283. SONG Qiong, ZHU Changchun, NIU Baoliang. The uncertainty evaluation of base 2 fast Fourier transfer [J]. Acta Metrologica Sinica, 2004, 3(25): 281-283.

[12]FUKUDA S. Pressure variations due to vapor condensation in liquid: II Phenomena at larger vapor mass flow flux [J]. Journal of the Atomic Energy Society of Japan, 1982, 24(6): 466-474.

[本刊相關文獻鏈接]

韓輝,何雅玲,唐桂華.硫酸蒸氣在換熱器表面沉積特性的數值研究.2013,47(11):7-13.[doi:10.7652/xjtuxb201311 002]

王斯民,文鍵.無短路區新型螺旋折流板換熱器換熱性能的實驗研究.2012,46(9):12-15.[doi:10.7652/xjtuxb201209 003]

李瑜,李亮,鐘剛云,等.末級透平對低壓缸氣動和凝結特性的影響.2012,46(7):16-20.[doi:10.7652/xjtuxb201207 004]

張僑禹,趙紅利,侯予.間壁式篩網網格換熱器的性能分析.2012,46(1):24-29.[doi:10.7652/xjtuxb201201005]

郭憲民,王善云,汪偉華,等.環境參數對空氣源熱泵蒸發器表面霜層影響研究.2011,45(3):30-34.[doi:10.7652/xjtuxb201103005]

何緯峰,戴義平,馬慶中,等.環境風影響下直接空冷單元背壓預測研究.2011,45(1):15-20.[doi:10.7652/xjtuxb2011 01004]

(編輯 荊樹蓉)

PressureOscillationInducedbySteamJetCondensationinWaterThroughaNozzle

WU Xinzhuang1,2,QIU Binbin2,CHONG Daotong2,YAN Junjie2

(1. State Nuclear Power Corporation Ltd., Shanghai Nuclear Engineering Research and Design Institute, Shanghai 200233, China;2. State Key Laboratory of Multiphase Flow in Power Engineering, Xi’an Jiaotong University, Xi’an 710019, China)

In order to obtain the pressure oscillation characteristics due to steam jet in water, an experiment was carried out to investigate the pressure oscillation characteristics at various axial positions and different water temperatures. The experimental system mainly consists of a steam generator, a surge tank, a nozzle, a water tank, instrumentations, a camera and a data acquisition system. The pressure oscillation amplitudes were measured and the main frequency was gained by the FFT method. The effects of the water temperature and position on the oscillation characteristic were analyzed. The results show that pressure oscillation amplitudes increased with water temperature, but a decreasing trend was found at high water temperatures. The main frequency decreased as water temperature increased, while the axial position had no effect on the main frequency. In addition, an existing correlation was used to predict the main frequency, and a good agreement was achieved between the predictions and the experiment data.

pressure oscillation; peak magnitude; main frequency

10.7652/xjtuxb201401009

2013-03-29。 作者簡介: 武心壯(1982—),男,博士,高級工程師。 基金項目: 國家核電技術公司員工自主創新項目專項資金資助項目(SNP-KJ-CX-2011-0008);國家自然科學基金資助項目(51125027)。

時間: 2013-10-17 網絡出版地址: http:∥www.cnki.net/kcms/detail/61.1069.T.20131017.0827.011.html

TK2

:A

:0253-987X(2014)01-0048-05