用于跨/超聲速壁板顫振精確分析的流-固耦合有限元算法

梅冠華,楊樹華,張家忠,孫旭,陳嘉輝

(1.西安交通大學能源與動力工程學院, 710049, 西安; 2.沈陽鼓風集團股份有限公司, 110869, 沈陽)

用于跨/超聲速壁板顫振精確分析的流-固耦合有限元算法

梅冠華1,楊樹華2,張家忠1,孫旭1,陳嘉輝1

(1.西安交通大學能源與動力工程學院, 710049, 西安; 2.沈陽鼓風集團股份有限公司, 110869, 沈陽)

為了精確和定量分析超聲速與跨聲速壁板的顫振特性,提出了一種基于有限元方法的流-固耦合算法,并用其研究了二維壁板顫振問題。首先,給出了壁板的von Kármán幾何大變形運動方程,以及高速氣流的歐拉控制方程。然后,采用標準有限元方法對壁板方程進行空間離散,而對流動控制方程的離散則運用雙時間步長推進的特征線分裂有限元方法,從而有效地消除了流場數值解的振蕩問題。隨后,采取松耦合算法實現了流體與固體間的數據傳遞。最后,運用所提出的算法對超聲速和跨聲速氣流作用下壁板的氣動彈性特性進行了分析,考察了歸一化動壓、預緊力和厚度比對系統特性的影響,并將該算法的分析結果與采用線性/非線性活塞理論和線性化勢流理論的經典壁板顫振結果進行了對比,證明該算法可以在較寬廣的馬赫數范圍內給出氣動力的精確描述,尤其適合于分析跨聲速氣流下的壁板氣動彈性響應。

壁板顫振;流-固耦合;特征線分裂算法;有限元方法;氣動彈性

在特定參數下,飛行器表面暴露于高速氣流中的壁板結構將產生自激振動現象,常稱作壁板顫振。這類振動是典型的氣動彈性問題,往往是由慣性力、彈性力和氣動力的共同作用而激發的,通常具有很強的非線性動力學特性,并將嚴重影響飛行器的疲勞壽命、飛行性能、飛行安全和乘坐品質。因此,深入研究壁板顫振問題對于高速飛行器的壁板設計、顫振抑制、疲勞壽命估計和顫振的合理利用都具有十分重要的意義[1-3]。

作為經典問題,壁板顫振已由眾多學者進行了深入細致的研究[4-10]。在大多數壁板顫振的研究中,壁板一般采用von Kármán幾何大變形理論描述,以便準確捕捉系統的各類復雜響應,氣動載荷大多采用簡化氣動力模型近似表達,如線性/非線性活塞理論[4,11]、線性化勢流理論[5-6]等,由此可推導出系統的偏微分控制方程。對于此類控制方程,常采用Galerkin方法、Rayleigh-Ritz方法、有限元方法(FEM)等將其離散為常微分控制方程,并運用各種頻域或時域分析工具進行研究。雖然這些簡化氣動力理論使用起來較為方便,然而其適用范圍和精度都較為有限,一般而言,線性活塞理論適用于1.45時,由于非線性效應變得十分顯著,氣動力常采用非線性活塞理論來描述。目前,尚沒有一個普遍適用于亞聲速、跨聲速、超聲速和高超聲速流動的簡化氣動力理論。此外,簡化氣動力理論給出的氣動載荷是與固體位移、速度及其偏導數相關的函數,而并非是通過計算流體動力學(CFD)所得出的,因此無法給出流場的細節信息,如黏性邊界層、旋渦、流動分離、激波等,進而無法準確分析流體與固體間的耦合機理。事實上,這些正是壁板顫振定量分析中的開放性問題。

近年來,伴隨著計算機軟、硬件水平的飛速發展,流-固耦合算法被逐漸用于分析壁板顫振問題。其中,氣動力由基于流體歐拉或Navier-Stokes控制方程的CFD方法獲得,同時將CFD與計算結構動力學(CSD)耦合起來研究壁板的氣動彈性響應。流-固耦合算法不僅廣泛適用于亞聲速、跨聲速、超聲速和高超聲速流動,可以在幾乎所有馬赫數范圍內給出氣動力的精確表達,而且還可以給出流場的細節描述,這些都是簡化氣動力理論所不能實現的。使用流-固耦合算法,Davis求解了二維壁板顫振問題,發現了許多不同于簡化氣動力理論的新現象[12-13];隨后,Gordiner研究了二維和三維壁板顫振問題,發現邊界層的存在推遲了顫振的發生[14];Hashimoto分析了跨聲速三維壁板顫振問題,在與他人實驗結果取得一致的同時,還發現湍流邊界層不僅對顫振可以起到穩定作用,在特定條件下還能引起不穩定效應[15]。

在目前的壁板顫振的流-固耦合研究中,對流場的求解大多采用有限差分法(FDM)和有限體積法(FVM),而采用FEM的較少。雖然FEM的推導過程相對煩瑣,計算時間也稍長,然而FEM有其獨特的優勢:①由于無須構造交錯網格,FEM的網格生成和數據結構較為簡單;②在已經生成的粗網格上,FEM可以通過選用高階單元來提高精度,而FDM和FVM則往往需要通過加密網格來提高精度;③由于FEM的普適性,可被廣泛用來處理多場耦合問題,尤其是流-固耦合問題。若能將流體和固體采用統一的FEM求解,就有可能實現流-固同步耦合求解,并在后續研究中引入系統自由度縮減方法[16],不僅能加快求解速度,更能提取出符合物理意義的氣動彈性模態信息。

由于流體控制方程中的非線性對流項往往會引起數值解的振蕩,因此標準Galerkin FEM不能直接用于求解流體控制方程。基于此,眾多改進的FEM被不斷提出,如流線迎風Petrov-Galerkin(SUPG)方法、Taylor-Galerkin(TG)方法、Galerkin最小二乘(GLS)方法等,其中特征線分裂(CBS)方法由Zienkiewicz首先提出,并用于求解對流擴散方程[17]。經過眾多學者的不斷發展和完善,迄今為止,特征線分裂有限元方法(CBS-FEM)已被廣泛應用于求解各類流動問題,例如不可壓縮流動、可壓縮流動、含激波的高速流動、湍流流動等。近年來,將CBS-FEM發展應用于求解動邊界問題,如流-固耦合問題和自由液面流動問題等,已成為新的研究熱點。

為了精確和定量分析超聲速與跨聲速壁板顫振特性,本文提出一種基于FEM的流-固耦合算法,并用來在時域內對二維壁板顫振問題進行分析。首先,分別采用von Kármán幾何大變形方程和歐拉方程來描述壁板變形和高速氣流。然后,對壁板控制方程采用標準FEM進行空間離散,對流體控制方程則運用雙時間步推進的CBS-FEM進行離散。隨后,采取松耦合算法實現流體與固體間的雙向耦合。最后,運用所提出的算法對超聲速和跨聲速氣流下壁板的氣動彈性響應進行分析,考察歸一化動壓、預緊力和厚度比對系統特性的影響,并對壁板的穩定性邊界進行計算。

1 壁板顫振模型及其數值解法

若三維壁板的展向尺寸遠大于其弦長,則可忽略展向效應,將其簡化為二維壁板,這給問題的分析帶來了很大便利。作為初步研究,先對二維壁板顫振問題進行分析,其模型如圖1所示:二維平板置于剛性平面上,其上表面處于沿x方向的高速來流中,下表面對應著空腔。流體的來流速度、馬赫數和密度分別為U∞、Ma∞和ρ∞,平板的長度、厚度、單位長度質量、彈性模量和泊松比分別為a、h、ρm、E和μ,平板兩端初始拉伸面內力為N0,上表面由流場所施加的氣動載荷為p,下表面空腔壓力與來流壓力相同,皆為p∞。

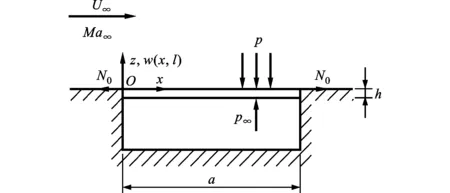
圖1 二維平面壁板顫振示意圖

對于厚度遠小于長度的壁板,即常見的薄板,可以采用Kirchhoff-Love假設,僅考慮其橫向運動w(x,t)。應變-位移關系采用von Kármán幾何大變形理論表示,則平板的控制方程為[4]

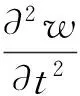
(1)

其中平板的彎曲剛度D=Eh3/[12(1-μ2)],大變形產生的中面拉伸載荷

(2)

氣動載荷

Δp=p-p∞

(3)

壁板的邊界條件可以為簡支或固支。對于簡支端,其數學表達式為w=0,?2w/?x2=0;對于固支端,其數學表達式為w=0,θ=?w/?x=0。

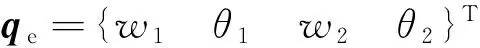
N1=1-3ξ2+2ξ3;N2=l(ξ-2ξ2+ξ3)

N3=3ξ2-2ξ3;N4=l(ξ3-ξ2)

采用標準Galerkin FEM對控制方程(1)進行變分以及空間離散,將其轉化為關于時間二階導數的常微分方程組

(4)

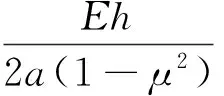
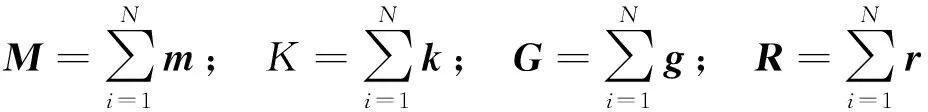
各單元矩陣的具體表達式為

q={w1,θ1,w2,θ2,…,wN+1,θN+1}T為壁板的整體位移。

對于該動力系統,只要給定初始條件,采用自適應Runge-Kutta積分方法數值求解即可。

2 流動控制方程及其數值解法

在高速流動問題中,黏性的影響相對較小,而可壓縮性的影響十分顯著,故為方便研究,可以采用可壓縮無黏Navier-Stokes方程,即歐拉方程來描述流場,其守恒形式為

連續方程

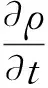
(5)

動量方程

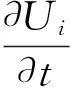
(6)

能量方程

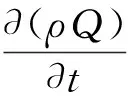
(7)

補充方程

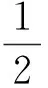
(8)

式中:ρ為流體密度;p為流體壓強;e為單位質量流體的內能;Q為單位質量流體的總能量;γ=1.4為空氣的比熱容比;xi、ui和Ui=ρui分別為坐標、速度和守恒速度。在二維流動中,下角標i=1,2分別對應著x和y方向。

流動方程的求解采用基于特征線分裂算法的有限元方法,將流場變量沿著特征線運動方向進行變換處理,從而可消除對流項,并有效避免數值解的振蕩。當前,在可壓縮流動問題求解中廣泛采用的是單時間步長推進的CBS-FEM,由于其大多采用完全顯式格式,使得時間步長的選取受限于收斂條件。此外,為方便計算,在求解過程中常進行質量集中處理,這種簡化對穩態問題沒有任何影響,因為隨著穩態解的收斂,時間變化項也會隨之消失。然而,對于瞬態問題而言,該近似所帶來的誤差相當嚴重,此時為獲得準確解,可引入附加的迭代過程。基于此,本文采用雙時間步長CBS-FEM來求解歐拉方程。事實上這是隱式格式算法,在每個物理時間步的推進過程中,通過引入一系列偽時間步的迭代過程,來獲得局部的偽定常收斂解[17-18]。這樣,真實時間步長的選取就不再受限于收斂條件,而且質量集中帶來的誤差也可有效消除。雙時間步長CBS-FEM算法的具體流程如下。

第1步

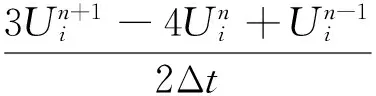
(9)

第2步

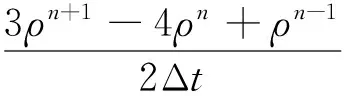
(10)

第3步

(11)

第4步

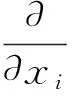
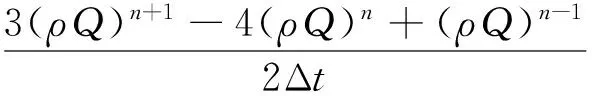
(12)

修正速度、密度和能量

(ρQ)m+1=(ρQ)m+Δ(ρQ)

計算壓力

(13)

式(9)～式(13)中:上角標n和n+1分別代表當前時刻和下一時刻,m和m+1分別對應前、后2個偽時刻;Δt為物理時間步長;Δτ為偽時間步長;θ1和θ2為松弛因子,一般選取θ1=1,θ2=0。

采用線性三角形單元剖分計算區域,則流體變量可表達為形函數和節點值相乘的形式

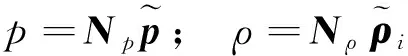
運用標準Galerkin有限元方法,將式(9)～式(12)進行變分和空間離散,并忽略高階項,即可得到雙時間步長推進CBS-FEM的離散格式。

一般而言,對于存在激波的流動問題,如果直接進行數值模擬,則解在激波附近會引起強烈的振蕩,影響收斂性。因此,必須添加合理的人工黏性項,選用合適的激波捕捉方法來抑制振蕩并捕捉激波。本文采用基于壓力二階導數的激波捕捉方法[17,19]。

壁板上方流場計算區域及網格剖分如圖2和圖3所示,遠場邊界位于25倍壁板弦長處。為了生成高質量網格并獲得精確的氣動載荷,將計算區域劃分為2個子區域:子域1為壁板上方0.5a高度的矩形區域,其余為子域2。對于子域1,流-固耦合界面和高度方向分別均布48和24個網格;對子域2,布置環繞子域1的48層C型網格。流場網格共計5 881個節點和11 520個三角形單元。

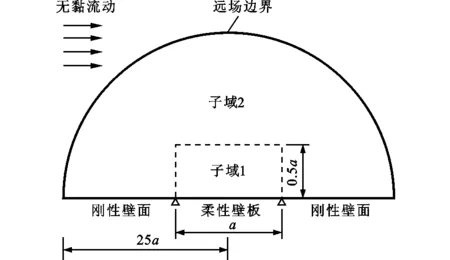
圖2 壁板上方流場計算區域(非等比例繪制)

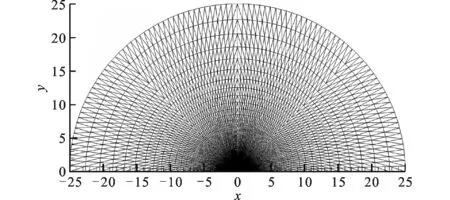
(a)整體網格

(b)局部網格

遠場邊界條件由Riemann無反射邊界條件給定[12]。壁板上游和下游皆為剛性壁面,在無黏流動中將其法向速度設為0即可。流-固交界面雖然也為壁面邊界條件,然而由于壁板運動的影響,將其給定為(u-us)·n=0,其中u為流體速度,us為壁板運動速度,n為壁板節點的法向量。

3 動網格及流-固耦合方式

隨著壁板的上下運動,流-固交界面也在不斷運動。在該類動邊界流動問題的計算過程中,如果規定動邊界上的節點隨邊界同步運動,將使得動邊界附近的網格單元發生扭曲變形甚至重疊,導致無法計算流場;如果規定流場網格固定不變,不隨邊界運動而移動,就會給邊界位置的捕捉帶來很大不便。常用的處理方法是采用動網格技術,讓動邊界上的網格節點隨著邊界同步運動,求解區域內部的節點也隨之相應調整,從而不僅可以準確地描述動邊界位置,還可以保證流體網格的質量。

由于該流-固耦合問題的特殊性——壁板僅在y方向產生位移,而且在壁板上方的子域1內均布了24層結構化流體網格,故僅需將壁板節點的位移在子域1內沿著y方向均分即可,這樣既能保證網格質量,又不會在動網格上耗費大量的計算時間。作為驗證,令壁板以w=0.05asin(2πx/a)形式彎曲,移動后的網格如圖4所示。整體和子域1內網格的最大單元偏斜度分別為0.568 2和0.485 7,遠小于0.9,說明雖然壁板發生了較大的變形,然而網格的質量仍得以較好地保持,這證實了動網格方法的可靠性。

圖4 動網格方法驗證

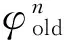
(14)

式中:Δxi為舊網格節點至新網格節點的位移。

流-固耦合的方式為松耦合,在每個時間步流體與固體相互交換一次數據,也稱為單步耦合,具體實施方法如下:

(1)將氣動載荷Δp傳遞給壁板;

(2)將壁板響應推進至下一時刻;

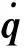
(4)移動流體網格;

(5)更新流場初值;

(6)將流場變量推進到下一時刻;

(7)繼續下一個時間步直到計算結束。

與緊耦合和同步耦合算法相比,松耦合使用起來較為方便,僅需對CFD和CSD的程序進行適當修改即可,同時它的計算速度較快,是一種應用較廣的雙向耦合算法。然而,由于在一個時間步長內流體和固體僅相互交換一次數據,且該數據并非是同一時刻的,因此兩者間存在著時間滯后,如果時間步長選取不當,很容易造成誤差累積并導致解的發散,故需要慎重選擇時間步長。經過不斷嘗試,最終將時間步長選取為ΔtU∞/a=0.01,這樣既能保證解的準確性,又不至于消耗過長的計算時間。對于該時間步長的獨立性驗證,將在下一節進行闡述。

4 數值模擬和結果分析

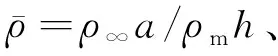
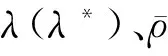
4.1 網格無關性分析和時間步長獨立性驗證

先分析流場網格的無關性,計算Ma∞=2時壁板在固定變形位置y=0.1asin(πx/a)上的穩態擾流問題。計算3種不同疏密的網格,即第2節給出的標準網格、疏網格、密網格,在其壁板邊界分別均布48、24和72個單元,得到壁面上的相對壓力分布情況,如圖5所示,可見在壁板前緣和后緣存在著2個明顯的激波。標準網格與密網格所得出的結果并無明顯差異,說明采用標準網格可以得到足夠精度的流場。

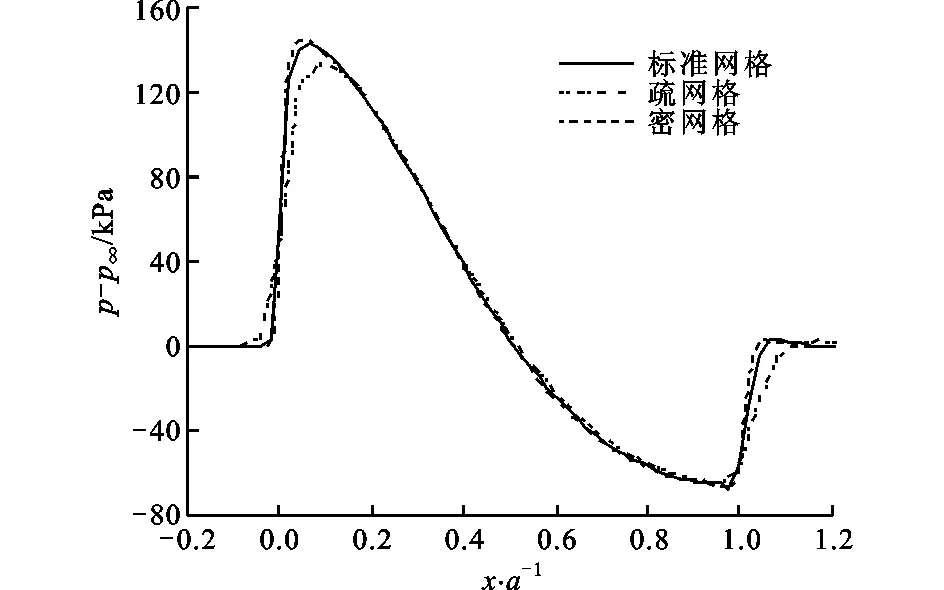
圖5 流場網格無關性分析

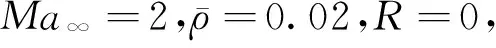
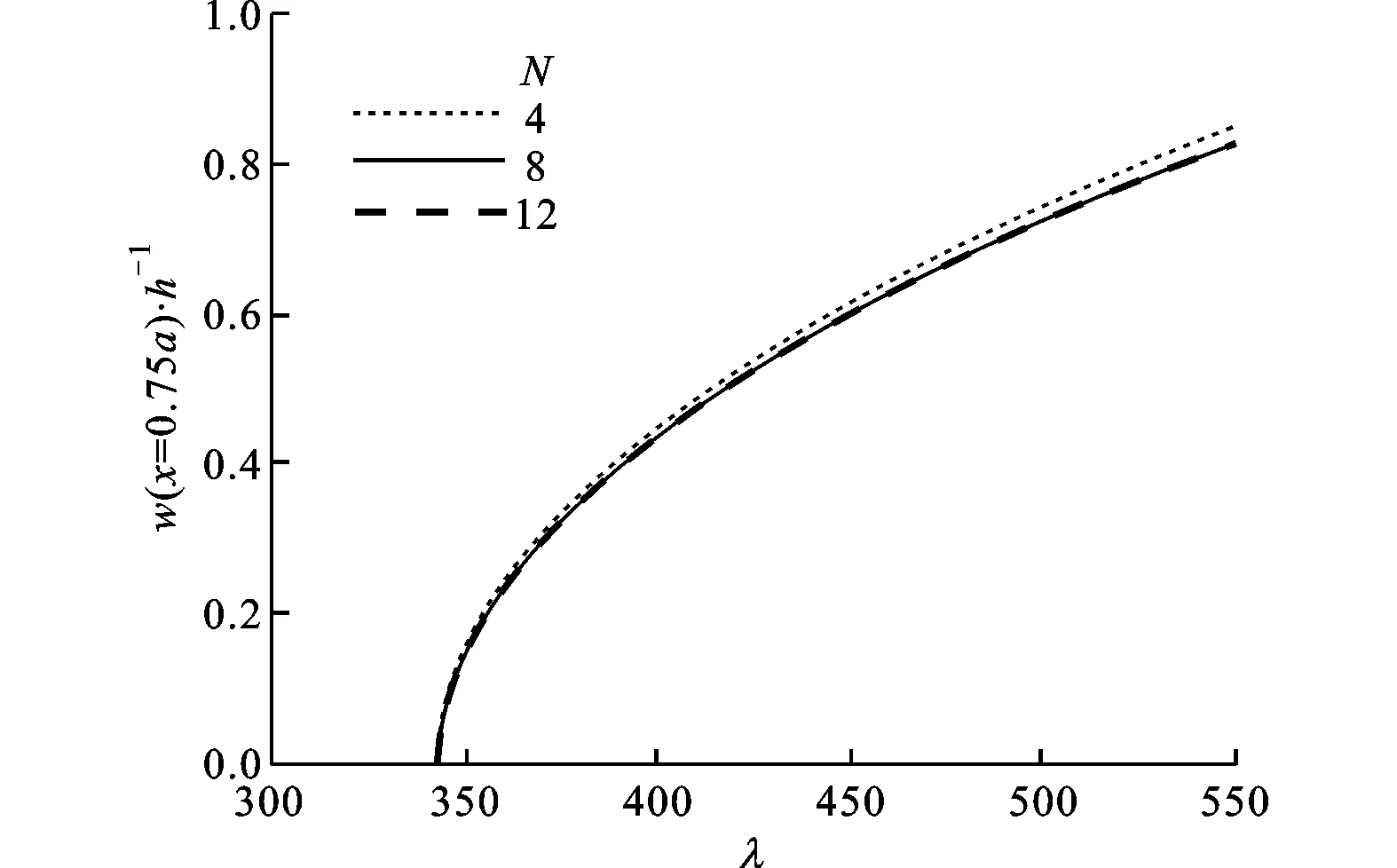
圖6 固體網格無關性分析

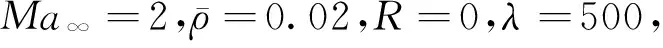
圖7 流-固耦合算法中時間步長的獨立性分析

4.2 超聲速氣流下的壁板響應

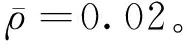
當歸一化預緊力R=0時,在較小的歸一化動壓λ下,初始擾動系統經過瞬態振動將恢復到初始位置,表現為平面穩定狀態。如圖8所示λ=300時的壁板響應,經過大約30至40個周期的瞬態振動,初始擾動被完全衰減,系統恢復到了平面穩定狀態。當λ逐漸增大并越過臨界值λcr,系統將發生Hopf分岔,由平面穩定狀態轉變為極限環顫振狀態。λ=500時的系統響應如圖9a所示,穩態極限環顫振的最大值和最小值分別為0.660和-0.679,后者的絕對值略大于前者,表明該振動關于中性面是非對稱的,這意味著壁板的正向運動和負向運動對于流場的影響是不同的。

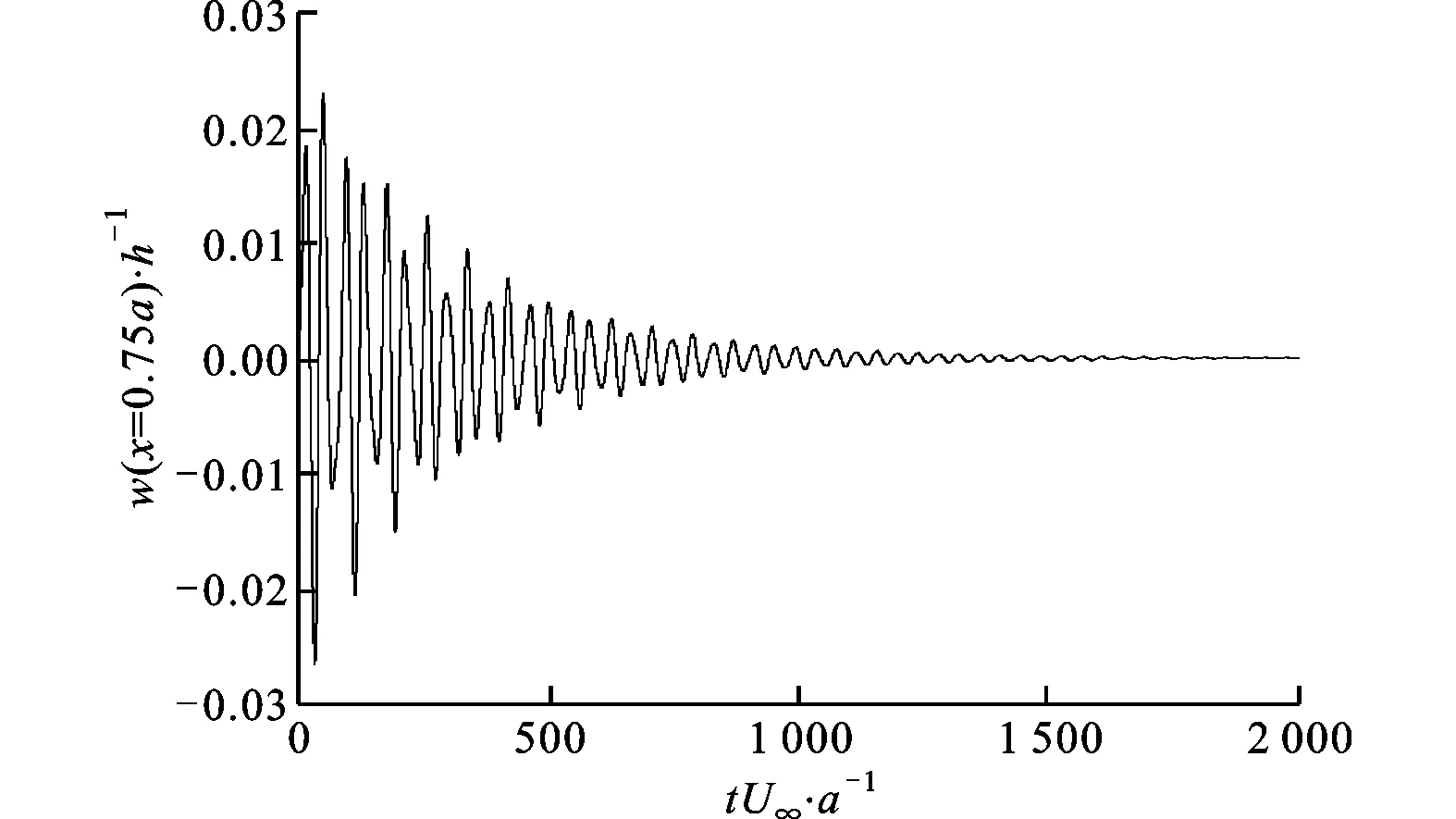
作為該振動的詳細分析,圖9b和圖9c分別給出了在一個周期內不同時刻的壁板變形和氣動載荷。從圖9b中可以看出,雖然不同空間質點的振幅不同,然而各質點在時間上的運動規律是相同的,即它們同時達到最大或最小位移,這是駐波的典型特征,因此可認為壁板振動呈現出了駐波的形式,其中最大振幅位于x=0.75a附近,最小振幅位于x=0.3a附近。圖9c所示的壓力波動也呈現出駐波的運動形式,壓力最大值約位于壁板末端x=a附近,且隨著壁板的上下運動在壁板尾緣附近表現為激波與膨脹波的交替變換。由于激波是流場中典型的非線性現象,在激波附近的流體被強烈壓縮,因此激波的存在對壁板的顫振具有重大影響。

(a)位移時間歷程

(b)一個周期內的瞬時壁板位移

(c)一個周期內的瞬時壁板表面壓力分布

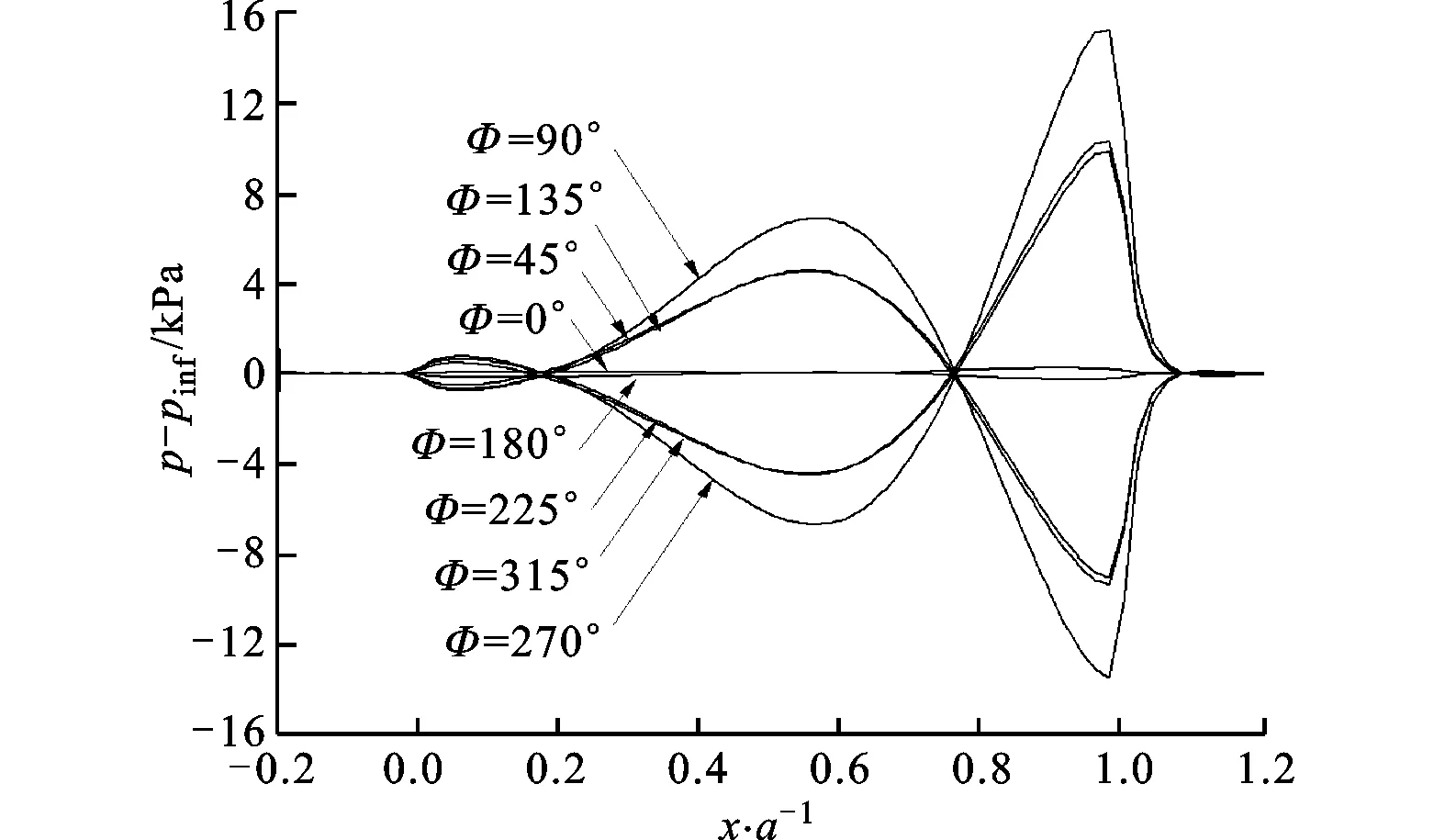
為考察系統對歸一化動壓的敏感性,研究了λ對極限環顫振的影響,結果如圖10所示。由圖中可以看出,在λ>λcr時壁板發生顫振,振幅與壁板厚度量級相同,且隨λ的增大而增大。圖10中還展示了線性和非線性活塞理論所得的結果[21]:線性活塞理論所得出的振動正負對稱,而非線性活塞理論所得振動的負向峰值絕對值大于正向峰值,這與本文算法的結果是一致的。定量來說,本文算法所得出的臨界動壓稍大,而振幅稍小。由于活塞理論沒有考察壁板不同時刻和不同空間質點間的相互影響,是一種基于當地流動和當前時刻的簡化氣動力理論,而基于歐拉方程的流-固耦合算法則直接從流體控制方程著手,綜合考慮了上述因素,利用CFD方法可以精確計算氣動載荷,因此這是兩者間存在差異的主要原因。

(a)位移時間歷程

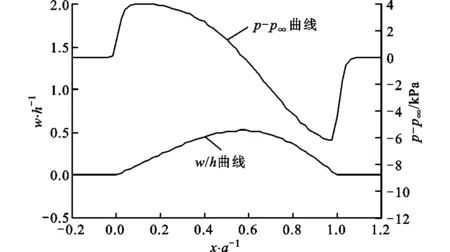
(b)屈曲變形和壓力分布

在施加了預緊力的情況下,壁板更多形式的響應將被激發出來。在較小的λ下,當歸一化預緊力R逐漸增大并跨過臨界值時,系統將發生靜態分岔,從平面穩定狀態轉變為屈曲狀態。例如:當λ=50和R=2時,壁板的位移時間歷程如圖11a所示,在動壓和預緊力的聯合作用下,系統最終到達穩定屈曲變形位置;壁板的最終變形和表面壓力分布如圖11b所示,最大變形位置大約位于x=0.6a附近,壁板的前緣和尾緣存在2個明顯的激波,其中尾緣處的激波比前緣處的激波更為劇烈,這可能是屈曲最大變形位置略向后偏移的結果。

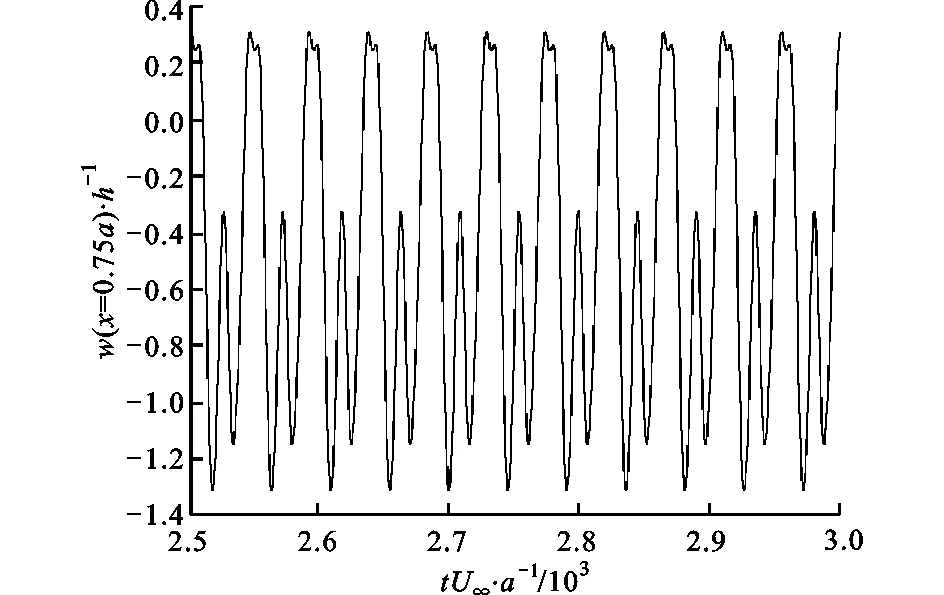
(a)位移時間歷程

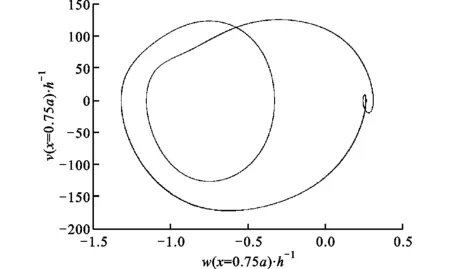
(b)相圖

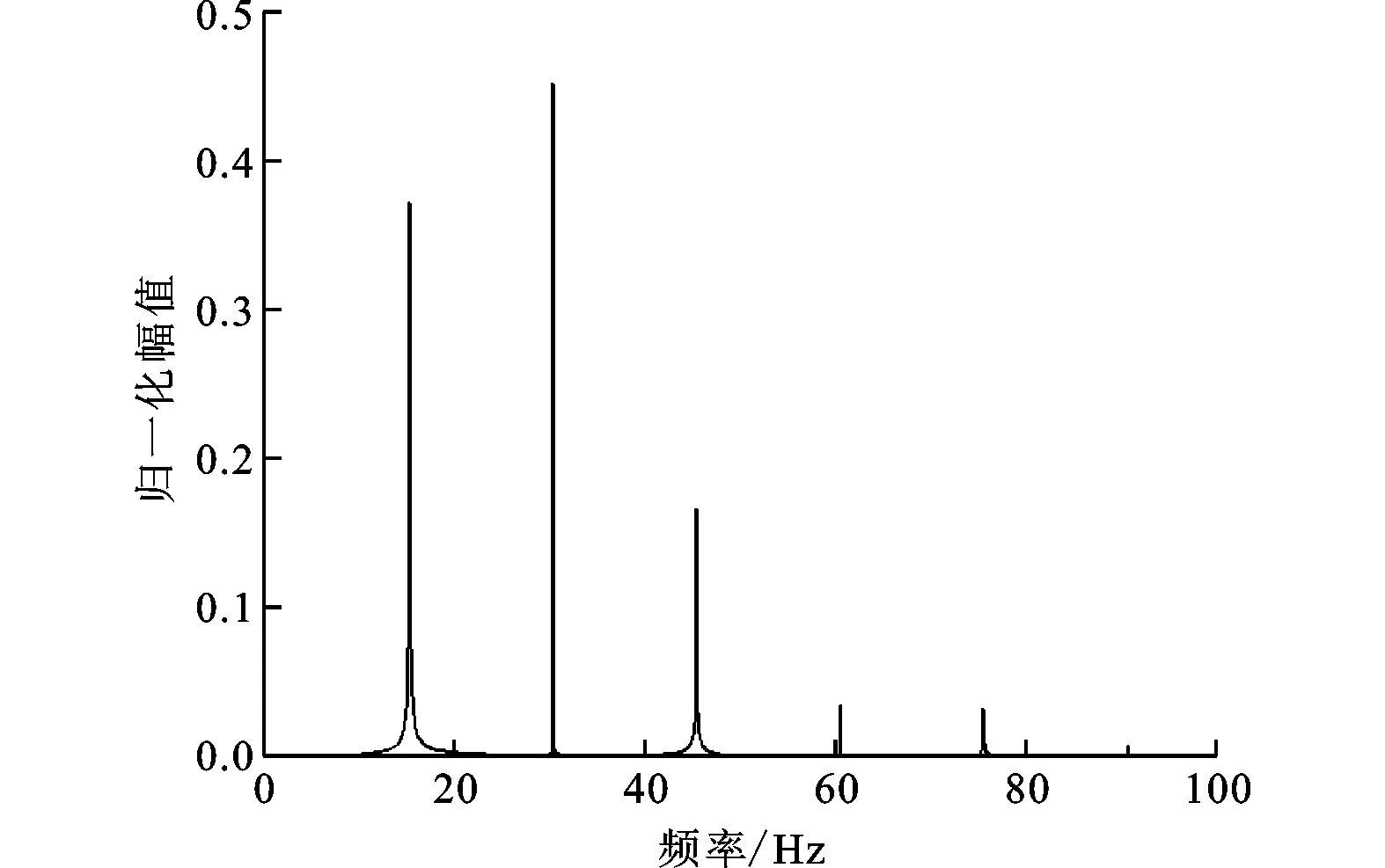
(c)頻譜分析

在特定的λ和R下,系統可表現出非線性復雜振動。例如:在λ=140和R=5時,壁板的穩態響應如圖12a所示,雖然振動為周期形式,然而振動方式卻表現出了極強的非線性特性;在圖12b所示的相圖中,不難發現該振動具有倍周期運動的特性;在圖12c所示的該振動的頻譜中包含了6階頻率分量,分別約為15、30、45、60、75和90 Hz,其中前3階頻率所占比重較大,后3階頻率的比重較小,由于頻率間呈現出1至6的整數倍關系,因此系統表現出了倍周期運動的特征。

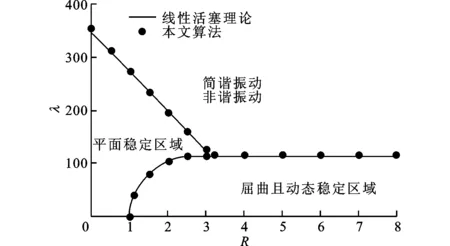
在R和λ所構成的參數平面上,對系統的平面穩定、屈曲、振動響應區域進行了劃分,如圖13所示:隨著R從0開始逐漸增大,壁板的顫振臨界動壓λcr逐漸降低,即預緊力的增加使得壁板更易發生顫振;隨著λ從0開始逐漸增大,壁板的屈曲臨界預緊力R逐漸增大,即氣動載荷的增加使得壁板不易發生屈曲。此外,本文算法所得結果與線性活塞理論所得結果是一致的。

4.3 跨聲速氣流下的壁板響應

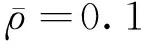
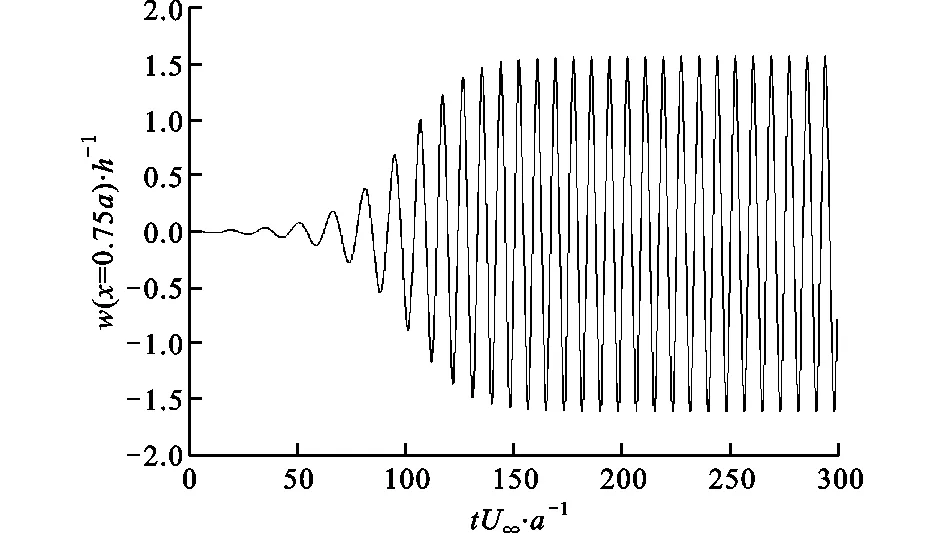
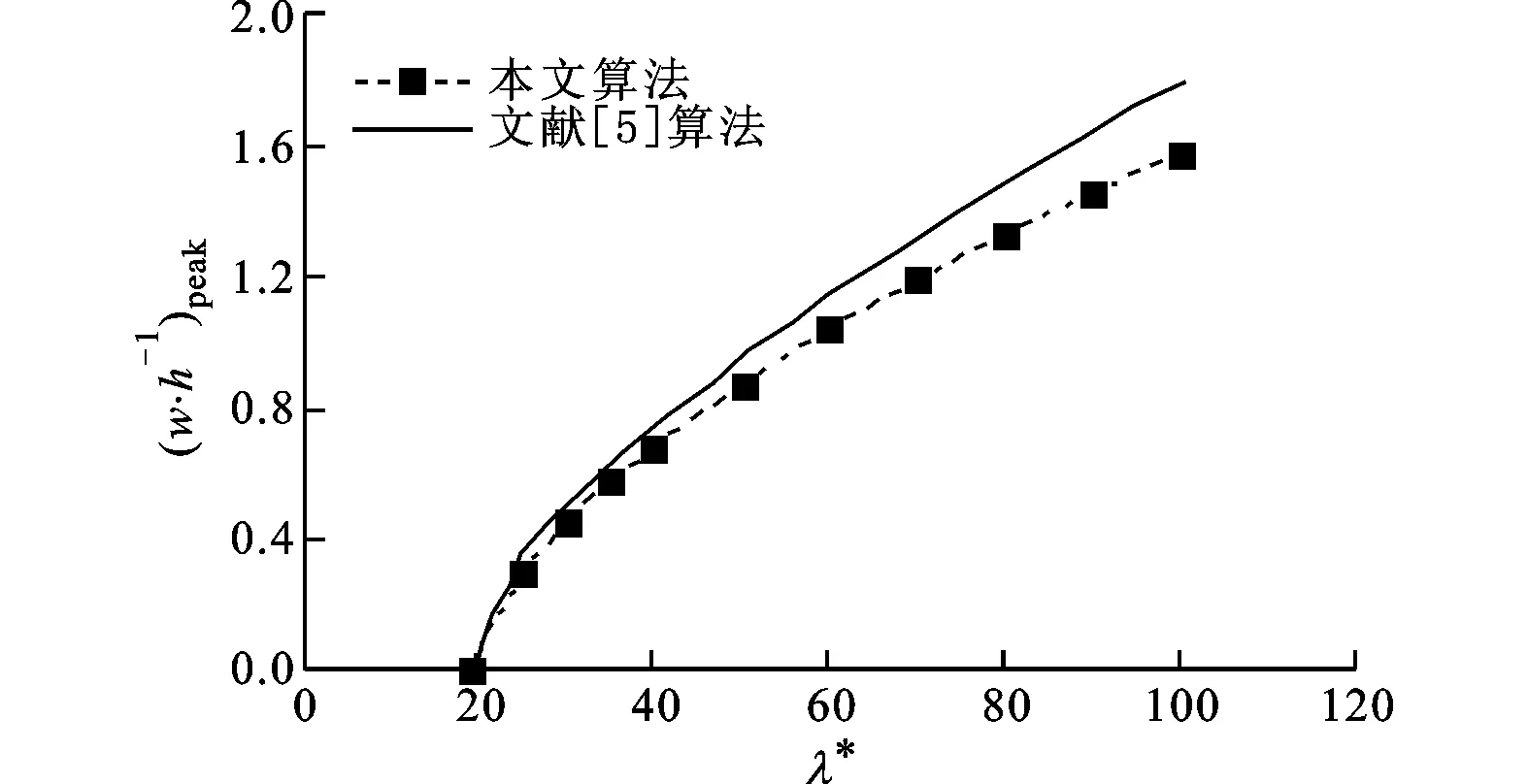
歸一化動壓λ*對于顫振幅值的影響如圖15所示:當λ*越過臨界值后,最大振幅隨著λ*的增加而增大,本文算法所得結果與文獻[5]采用線性化勢流理論所得結果吻合較好,然而隨著λ*的增大,兩者間的差距逐漸增大,這可能是由于線性化勢流理論是從擾動速度和勢流理論的角度來推導氣動力的,并不能準確反映整體流場的狀況,與歐拉方程算得的氣動力仍存在一定差距的緣故。

對于Ma∞<1(如Ma∞=0.8和Ma∞=0.9)的跨聲速氣流,系統失穩后壁板將偏離初始位置,根據初始條件的不同到達正向或是負向屈曲變形位置。以位于海平面的鋁板為例,當Ma∞=0.9和h/a=0.004時,壁板的屈曲響應如圖16所示,可以看到其正向屈曲變形略大于負向屈曲變形。

關于系統對厚度比的敏感性,圖17給出了在Ma∞=0.8和Ma∞=0.9時h/a對壁板正向和負向屈曲變形的影響:最大屈曲變形隨著h/a的增大而減小,這是因為較小的h/a意味著壁板相對剛度較小,更容易發生屈曲;Ma∞=0.8時正、負屈曲變形近乎對稱,而Ma∞=0.9時正向變形要大于負向變形,這說明Ma越接近1,系統變得越復雜。此外,本文算法所得結果與文獻[13]的結果相當一致。

圖18顯示了Ma∞=0.8～1.4時跨聲速氣流作用下壁板的穩定性邊界。在Ma∞=1.0的聲速氣流附近,臨界動壓明顯降低,穩定性曲線在此處形成了一個“凹坑”,通常稱為“跨聲速凹坑”,因此對壁板顫振的研究設計者來說,聲速附近的臨界動壓是需要仔細考察的。本文算法所獲得的穩定性邊界與文獻[13]的結果亦相當一致。

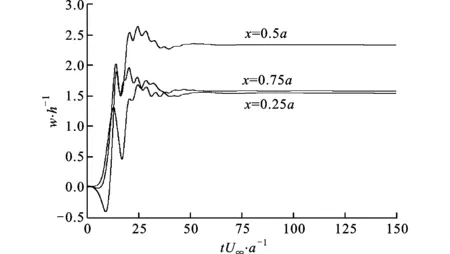
(a)正向屈曲

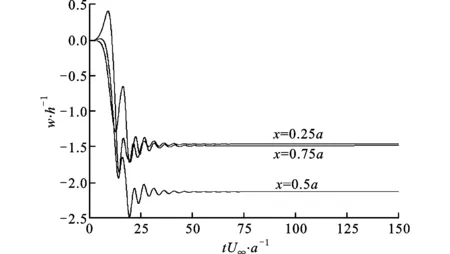
(b)負向屈曲Ma∞=0.9, h/a=0.004, 海平面鋁板

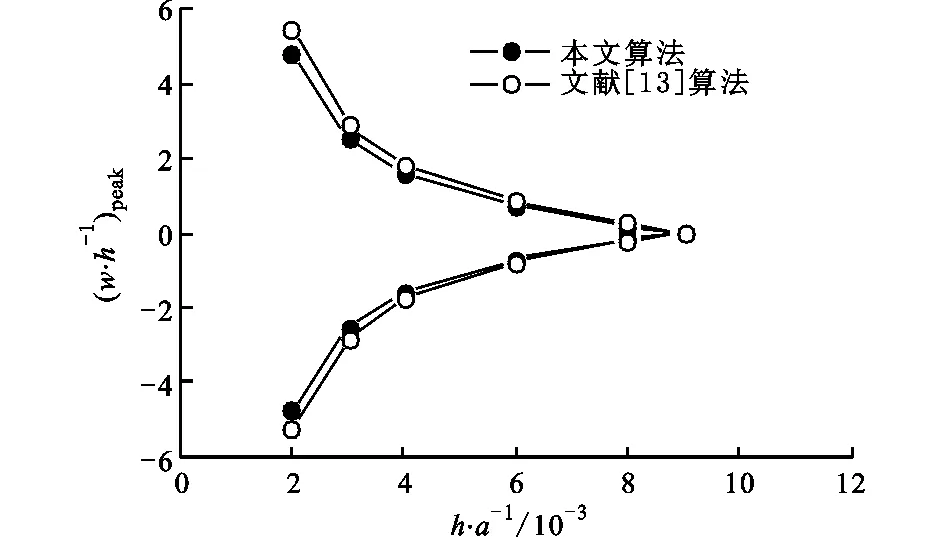
(a)Ma∞=0.8

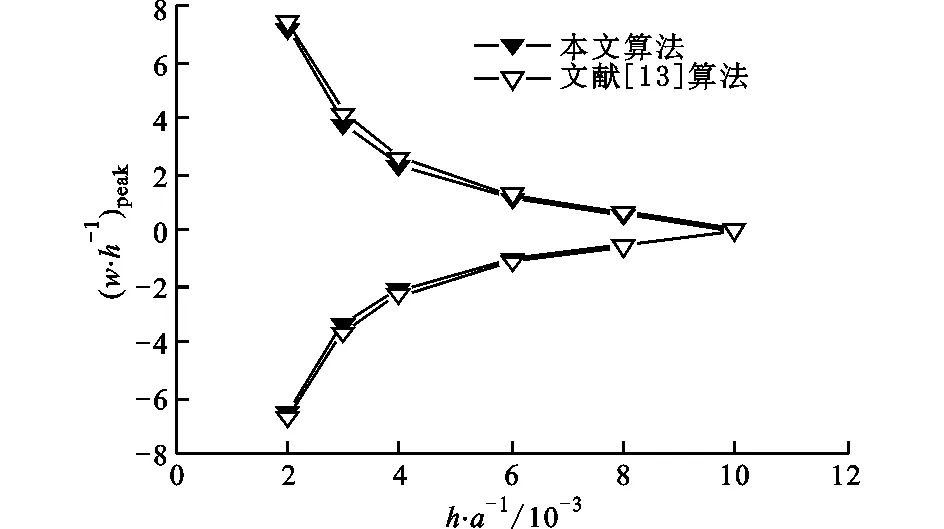
(b)Ma∞=0.9

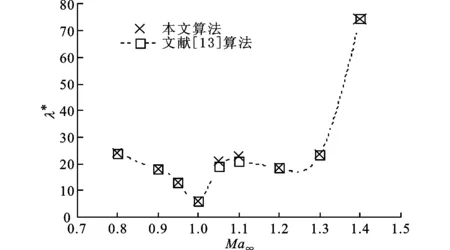
圖18 壁板的穩定性邊界

5 結論與展望

為了精確定量分析超聲速和跨聲速壁板的顫振特性,本文提出了一種基于有限元方法的流-固耦合算法,并用其研究了二維壁板顫振問題。該算法成功消除了流體方程中對流項所引發的數值振蕩,并實現了流體和固體間的雙向數據交換。通過對數值結果進行分析,所得主要結論如下:

(1)在馬赫數為2的超聲速氣流下,當歸一化動壓越過臨界值后,系統由平面穩定狀態轉變為極限環顫振狀態,振幅隨動壓增大而增大,且負向峰值的絕對值略大于正向峰值。對典型極限環顫振的分析發現:一個周期內壁板變形和氣動載荷皆呈現駐波的運動形式;在歸一化預緊力與歸一化動壓的共同作用下,系統可表現為屈曲或非簡諧復雜振動;激波對壁板顫振特性的影響較為顯著。

(2)在馬赫數為1.2的跨聲速氣流下,壁板響應與馬赫數為2的系統類似,只是此時系統對外界擾動反應較快,達到穩態響應所需的瞬態過程較短。

(3)在馬赫數為0.8和0.9的亞聲速氣流下,壁板失穩后表現為正向或負向的屈曲變形,正、負位置由初始條件所決定,且屈曲變形隨著壁板厚度比的減小而增大。

(4)對馬赫數在0.8至1.4之間的系統的穩定性邊界進行了計算,精確捕捉到了“跨聲速凹坑”現象。

(5)通過與采用線性/非線性活塞理論和線性化勢流理論的經典壁板顫振結果進行對比,表明本文算法可在更為寬廣的馬赫數范圍內給出氣動載荷的精確描述,尤其適合于分析跨聲速氣流下的壁板氣動彈性特性。

作為初步探索,本文對流動采用了歐拉方程描述,下一步將采用完全Navier-Stokes方程,并考察湍流的影響,以更加準確地描述流場和氣動載荷。此外,流-固耦合的計算過程耗費了大量的計算時間,未來將引入有效的系統自由度縮減方法,在保證計算精度的同時實現節省計算時間的目的。本文的工作僅對固體的氣動彈性特性進行了分析,今后將對流動的穩定性與失穩機理展開深入研究。

[1] 梅冠華, 張家忠. 時滯慣性流形在三維壁板顫振數值分析中的應用 [J]. 西安交通大學學報, 2011, 45(9): 40-46. MEI Guanhua, ZHANG Jiazhong. Numerical analysis of 3-D panel flutter by inertial manifolds with delay [J]. Journal of Xi’an Jiaotong University, 2011, 45(9): 40-46.

[2] 楊智春, 夏巍, 孫浩. 高速飛行器壁板顫振的分析模型和分析方法 [J]. 應用力學學報, 2006, 23(4): 537-542. YANG Zhichun, XIA Wei, SUN Hao. Analysis of panel flutter in high speed flight vehicles [J]. Chinese Journal of Applied Mechanics, 2006, 23(4): 537-542.

[3] MEI Guanhua, ZHANG Jiazhong, WANG Zhuopu. Numerical analysis of panel flutter on inertial manifolds with delay [J]. Journal of Computational and Nonlinear Dynamics, 2013, 8(2): 021009.1-021009.11.

[4] DOWELL E H. Nonlinear oscillations of a fluttering plate [J]. AIAA Journal, 1966, 4(7): 1267-1275.

[5] DOWELL E H. Nonlinear oscillations of a fluttering plate: II [J]. AIAA Journal, 1967, 5(10): 1856-1862.

[6] DOWELL E H. A review of the aeroelastic stability of plates and shells [J]. AIAA Journal, 1970, 8(1): 385-399.

[7] OLSON M D. Finite element approach to panel flutter [J]. AIAA Journal, 1967, 5(12): 226-227.

[8] OLSON M D. Some flutter solutions using finite element [J]. AIAA Journal, 1970, 8(4): 747-752.

[9] MEI Chuh, ABDEL-MOTAGLY K, CHEN R. Review of nonlinear panel flutter at supersonic and hypersonic speeds [J]. ASME Applied Mechanics Reviews, 1999, 52(10): 321-332.

[10]CHENG Guangfeng, MEI Chuh. Finite element modal formulation for hypersonic panel flutter analysis with thermal effects [J]. AIAA Journal, 2004, 42(4): 687-695.

[11]ASHLEY H, ZARTARIAN G. Piston theory: a new aerodynamic tool for the aeroelastician [J]. Journal of the Aeronautical Science, 1956, 23(12): 1109-1118.

[12]DAVIS G A, BENDIKSEN O O. Unsteady transonic two-dimensional Euler solutions using finite elements [J]. AIAA Journal, 1993, 31(6): 1051-1059.

[13]DAVIS G A. Transonic aeroelasticity solutions using finite elements in an arbitrary Lagrangian-Eulerian formulation [D]. Los Angeles, USA: University of California, 1994.

[14]GORDINER R E, FITHEN R. Coupling of a nonlinear finite element structural method with a Navier-Stokes solver [J]. Computers and Structures, 2003, 81(2): 75-89.

[15]HASHIMOTO A, AOYAMA T. Effects of turbulent boundary layer on panel flutter [J]. AIAA Journal, 2009, 47(12): 2785-2791.

[16]ZHANG Jiazhong, REN Sheng, MEI Guanhua. Model reduction on inertial manifolds for N-S equations approached by multilevel finite element method [J]. Communications in Nonlinear Science and Numerical Simulation, 2011, 16(1): 195-205.

[17]ZIENKIEWICZ O C, TAYLOR R L, NITHIARASU P. The finite element method for fluid dynamics [M]. 6th ed. Singapore: Elsevier Pte Ltd., 2009: 195-211.

[18]NITHIARASU P. An efficient artificial compressibility (AC) scheme based on the characteristic based split (CBS) method for incompressible flows [J]. International Journal for Numerical Methods in Engineering, 2003, 56(13): 1815-1845.

[19]NITHIARASU P, ZIENKIEWICZ O C, SATYASAI B V K, et al. Shock capturing viscosities for the general fluid mechanics algorithm [J]. International Journal for Numerical Methods in Fluids, 1998, 28(9): 1325-1353.

[20]孫旭, 張家忠. 具有運動邊界的不可壓縮黏性流動的CBS有限元解法 [J]. 西安交通大學學報, 2011, 45(1): 99-104. SUN Xu, ZHANG Jiazhong. A characteristic-based split-FEM scheme for incompressible viscous flow with moving boundaries [J]. Journal of Xi’an Jiaotong University, 2011, 45(1): 99-104.

[21]EASTEP F E, MCINTOSH S C. Analysis of nonlinear panel flutter and response under random excitation or nonlinear aerodynamic loading [J]. AIAA Journal, 1971, 9(3): 411-418.

(編輯 葛趙青)

AFluid-StructureCouplingAlgorithmBasedonFiniteElementMethodforPreciseAnalysisofTransonicandSupersonicPanelFlutter

MEI Guanhua1,YANG Shuhua2,ZHANG Jiazhong1,SUN Xu1,CHEN Jiahui1

(1. School of Energy and Power Engineering, Xi’an Jiaotong University, Xi’an 710049, China;2. Shenyang Blower Works Group Corporation, Shenyang 110869, China)

To analyze the supersonic and transonic panel flutter behavior quantitatively and accurately, a fluid-structure coupling algorithm based on the finite element method (FEM) is proposed for the two-dimensional panel flutter problem. First, the von Kármán’s large deformation theory is adopted to model the panel, and the high speed air flow is approached by the Euler equations. Then, the equation of panel is discretized spatially by the standard FEM, and the equations of fluid are discretized by the characteristic-based split finite element method (CBS-FEM) with dual time stepping, thus the numerical oscillation often encountered in numerical simulation of fluid flow can be eliminated. Furthermore, a loose coupling algorithm is applied to the data exchange between the fluid and the structure. Finally, the proposed algorithm is used to investigate the aeroelastic behavior of the panel in supersonic and transonic air flows and the influences of the non-dimensional dynamic pressure, pre-tightening force and thickness ratio on the system. The results are compared with those of the classical panel flutter analyses using linear/nonlinear piston theory and linearized potential flow theory. It shows that the proposed algorithm enables to obtain accurate aerodynamic pressure in a wide range of Mach numbers, especially for the analysis of panel aeroelasticity in transonic air flows.

panel flutter; fluid-structure interaction; characteristic-based split method; finite element method; aeroelasticity

10.7652/xjtuxb201401013

2013-03-29。 作者簡介: 梅冠華(1984—),男,博士生;張家忠(通信作者),男,教授,博士生導師。 基金項目: 國家“973計劃”資助項目(2012CB026002);國家“863計劃”資助項目(2012AA052303)。

時間: 2013-10-22 網絡出版地址: http:∥www.cnki.net/kcms/detail/61.1069.T.20131022.1113.003.html

O323

:A

:0253-987X(2014)01-0073-11