輸電線路桿塔構件可靠度校準

馮云芬，貢金鑫，李宏男，張子引

(1.大連理工大學建設工程學部，遼寧省大連市 116024；2.國網北京經濟技術研究院，北京市 102209)

輸電線路桿塔構件可靠度校準

馮云芬1，貢金鑫1，李宏男1，張子引2

(1.大連理工大學建設工程學部，遼寧省大連市 116024；2.國網北京經濟技術研究院，北京市 102209)

為確定跨越高速鐵路輸電線路的可靠度水平，分析計算桿塔構件荷載、抗力的統計參數，對按現行規范設計的輸電線路桿塔構件的可靠度進行了校準。分析表明，在永久荷載與風荷載組合下，構件軸心受力強度的可靠指標平均約為3.10，構件軸心受壓穩定的可靠指標平均約為2.99；在永久荷載與風荷載和覆冰荷載的組合下，構件軸心受力強度的可靠指標平均約為3.35，構件軸心受壓穩定的可靠指標平均約為3.20。永久荷載與風荷載組合時我國輸電線路桿塔桿件的可靠度水平比建筑鋼結構的可靠度略低；永久荷載與風荷載組合及永久荷載、風荷載與覆冰組合時，我國輸電線路桿塔桿件的可靠度水平與美國桿塔構件的可靠度水平相近，比加拿大桿塔構件的高。

輸電線路；桿塔構件；可靠度；校準

0 引 言

隨著我國經濟的高速發展，對電力的需求呈直線增長趨勢，因此電力系統的發展成為一種必然趨勢。輸電線路體系是高負荷電能輸送的載體，近年來逐漸趨于向大型化復雜化方向發展。因此，對輸電塔線路體系的設計理論、結構安全性都提出了新的要求。與此同時，近年來隨著我國高速鐵路的迅速發展，輸電線路跨越高鐵的情況經常出現。為保證高鐵的安全運行，對輸電線路跨越提出了更高的要求。因為鐵路基礎設施與輸電線路采用不同的設計方法，設計規范中材料強度的取值、分項系數或安全系數的含義不同，單從設計規范出發并不能明確鐵路設施與輸電線路的安全度。因此，需要采用同一個尺度進行分析和協調。

自20世紀80年代以來，可靠度理論在結構設計和規范中的應用得到了很大發展。結構可靠度理論是用概率方法描述結構的安全性，綜合考慮了荷載、材料性能、幾何尺寸、計算方法等不確定性，可靠指標能夠作為一個統一的尺度衡量不同結構的安全性。從國際范圍講，結構可靠度理論目前在建筑、橋梁等領域的應用相對比較成熟，然而在輸電線路體系的應用尚處于啟動狀態，一些學者已對此進行了探討[1-8]。國外一些電力系統的設計規范正向基于可靠度理論的設計方法過渡，如美國標準NESC C2—2002《美國國家電力安全規范》[9]和ASCE 74—2009《輸電線路結構荷載設計導則》[10]、加拿大規范CSA C22.3 No. 1—2001《高架線路系統》[11]、歐洲規范EN 50341《超AC 45KV架空輸電線路》[12]和國際標準IEO 606826—2003《架空輸電線路設計標準》等[13]。在鐵路工程領域，我國在20世紀90年代頒布了GB 50216—94《鐵路工程結構可靠度設計統一標準》，自2011年開始，鐵路工程領域啟動了鐵路工程設計規范由容許應力或安全系數設計法向可靠度設計法轉軌的工作。

為適應我國電力系統由傳統的高壓、超高壓輸電技術向特高壓輸電技術發展，滿足跨越高速鐵路輸電線路的安全要求，對跨越高速鐵路的輸電線路的可靠度進行了研究。本文的目的是確定按現行DL/T 5154—2002《架空送電線路桿塔結構設計技術規定》設計的輸電線路桿塔構件的可靠度水平。

1 荷載效應和抗力統計參數

輸電線路體系由輸電桿塔、絕緣子、金具和導、地線組成。桿塔構件應具有能夠承受自身重力、風荷載、覆冰荷載、溫度等作用的能力。對輸電線路桿塔構件及各組成部分進行可靠度分析和設計，首先要確定線路荷載效應和抗力的概率分布和統計參數。

1.1 荷載效應的統計參數

荷載效應是荷載使結構或構件產生的內力、變形等，一般認為荷載效應與荷載的概率分布是一致的。因此研究荷載效應的概率分布，只需研究荷載的概率分布。荷載的統計參數一般用均值系數(平均值與標準值的比值)和變異系數(標準差與平均值的比值)來表示。

桿塔設計中為便于荷載組合，荷載往往是按方向進行分類的。由于不同荷載的概率特性不同，可靠度分析中是按荷載隨時間變化的特性進行分類的，即將荷載分為永久荷載、可變荷載(風荷載和覆冰荷載)[14]。

1.1.1 永久荷載

在輸電線路中，永久荷載G包括桿塔構件、絕緣子、導地線等的自重。根據以往的統計資料，自重一般服從正態分布。參考建筑結構的統計分析結果，取自重的均值系數kG=1.06，變異系數δG=0.07。

1.1.2 風荷載

風荷載W是輸電線路承受的主要可變荷載之一。風荷載對輸電線路的作用機理比較復雜，輸電線路采用的風荷載計算方法與建筑結構相同，所以輸電線路可靠度分析時風荷載采用與建筑結構相同的概率分布和統計參數。風荷載服從極值I型分布。設計中考慮下面風荷載的2種荷載組合。

(1) 自重與風組合。

當自重與風荷載組合時，采用30 m/s風速作為代表風速，將該風速作為對應于設計基準期的標準值Wk的標準風速。采用建筑結構的統計參數，風荷載均值系數和變異系數為：kWT=0.908、δWT=0.193。

(2) 自重、風荷載和覆冰荷載組合。

當自重與風荷載和覆冰荷載組合時，采用10 m/s的風速作為代表風速，風荷載降低。假定10 m/s的風速為1年中覆冰最大的1個月的最大風速，則風荷載平均值按式(1)估算：

(1)

式中：μWt為永久荷載與風荷載和覆冰組合中風荷載的平均值；μWT和σWT為永久荷載與風荷載組合中風荷載的平均值和標準差；αWT為極值Ⅰ型分布的尺度參數；t取1個月；T為風荷載重現期，取50年。

永久荷載與風荷載和覆冰荷載組合時，風荷載的均值系數為0.034。假定此時的風荷載變異系數仍為0.193。

1.1.3 覆冰荷載

天空中的“過冷卻”水滴、濕雪碰到溫度較低的導地線或絕緣子等部件時，便會在其表面凍結成冰，稱之為覆冰。導線覆冰的機理非常復雜，影響導線覆冰的因素也很多，主要有氣象條件、地形及地理條件、海拔高度、凝結高度、導線懸掛高度、導線直徑、導線扭轉性能、風速風向、水滴直徑、電場強度及負荷電流等。

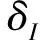
1.2 抗力統計參數

抗力為結構或元件抵抗荷載作用的能力，其不確定性來自于3個方面，即材料性能不確定性、幾何尺寸不確定性和計算模式不確定性。同荷載效應一樣，抗力的統計參數也用均值系數和變異系數表示。

1.2.1 構件軸心受力

根據DL/T 5154—2002《架空送電線路桿塔結構設計技術規定》，并考慮公式的計算誤差，桿塔構件軸心受力時的抗力可表示為

R=ΩP 1mAf

(2)

式中：ΩP 1為軸心受力強度時抗力計算模式不定性系數(隨機變量)；m為構件強度折減系數(常數)；A為構件截面面積(隨機變量)；f為構件材料強度(隨機變量)。

抗力的均值系數和變異系數為：

(3)

(4)

式中：μR、μA和μf分別為抗力、構件截面面積和鋼材強度的平均值；kP1、kA、kf和δP1、δA、δf分別為計算模式不定性、截面面積和鋼材強度的均值系數和變異系數；Rk、Ak和fk分別為抗力、截面面積和鋼材強度的標準值，其中fk按規范DL/T 5154—2002取值。各變量的統計參數見表1[16]。

由式(3)和式(4)確定的桿塔構件軸心受力時抗力的統計參數為kR=1.134，δR=0.117，抗力服從對數正態分布。

表1 構件軸心受力時抗力的統計參數

1.2.2 構件受壓穩定

同樣，根據DL/T 5154—2002《架空送電線路桿塔結構設計技術規定》，考慮公式的計算誤差，桿塔構件軸心受壓構件的穩定承載力表示為

R=ΩP2φmNAf

(5)

式中：ΩP2為抗力計算模式不定性系數(隨機變量)；φ為軸心受壓構件穩定系數(隨機變量)；mN為系數(常數)；A為構件截面面積(隨機變量)；f為構件材料強度(隨機變量)。

抗力的平均值和變異系數為：

(6)

(7)

式中：μφ、δφ和kφ分別為構件受壓穩定性系數的平均值、變異系數和均值系數；kP2和δP2分別為軸心受壓穩定時抗力計算模式不定性的均值系數和變異系數；φk為穩定性系數的標準值。其中，kφ和δφ是按下述方法確定的，其他變量的統計參數見表1和表2。

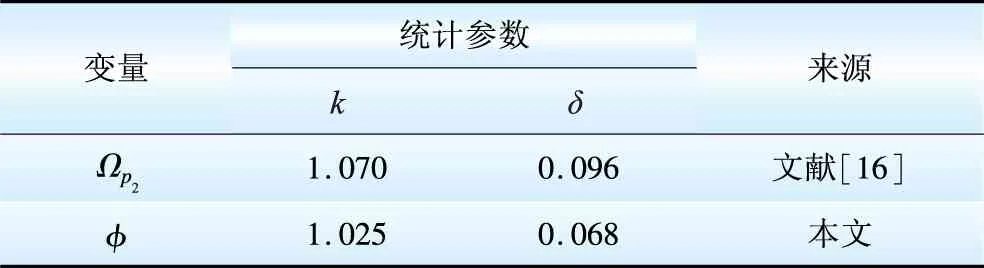
表2 構件軸心受壓穩定抗力的統計參數

根據規范DL/T5154—2002[17]附錄D，軸心受壓構件穩定系數φ按式(8)計算：

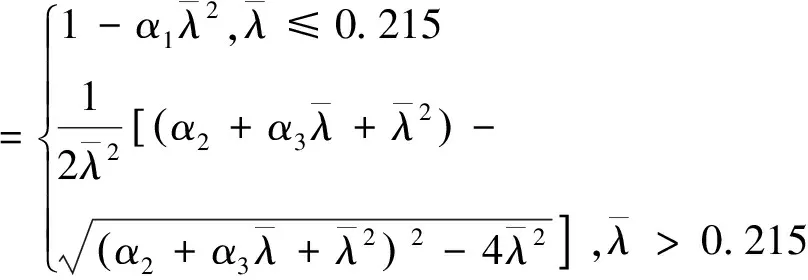
(8)

其中：

(9)

式中：λ為構件長細比；fy為鋼材屈服強度；E為鋼材彈性模量；α1、α2和α3為系數，根據DL/T 5154—2002附錄D中表D3的截面分類按表D4取值[17]。

由于在式(8)中，穩定系數φ是用分段函數表示的，直接采用數學方法確定φ的概率分布函數及平均值和變異系數比較復雜。為了確定參數穩定系數φ的均值系數kφ和變異系數δφ，將鋼材屈服強度fy和彈性模量E作為隨機變量，根據fy和E的概率分布通過Monte Carlo模擬產生10 000組fy和E的隨機數，將其代入式(8)得到φ的樣本值。通過統計分析分別確定了構件長細比λ為10、50和100時軸心受壓構件穩定系數的統計參數，如表3所示。圖1給出了λ=50時b類截面在不同鋼號下比值φ/φk的直方圖。根據表3的分析結果，φ的均值系數取為kφ=1.025，變異系數δφ取為0.068。

表3 φ/φk的平均值及變異系數

圖1 b類截面長細比λ=50時φ/φk的頻率直方圖

由式(6)和式(7)求得的桿塔構件軸心受力時穩定抗力的統計參數kR=1.185，δR=0.150。

1.3 荷載、抗力統計參數匯總

輸電線路荷載及塔桿構件抗力的統計參數和概率分布匯總于表4。

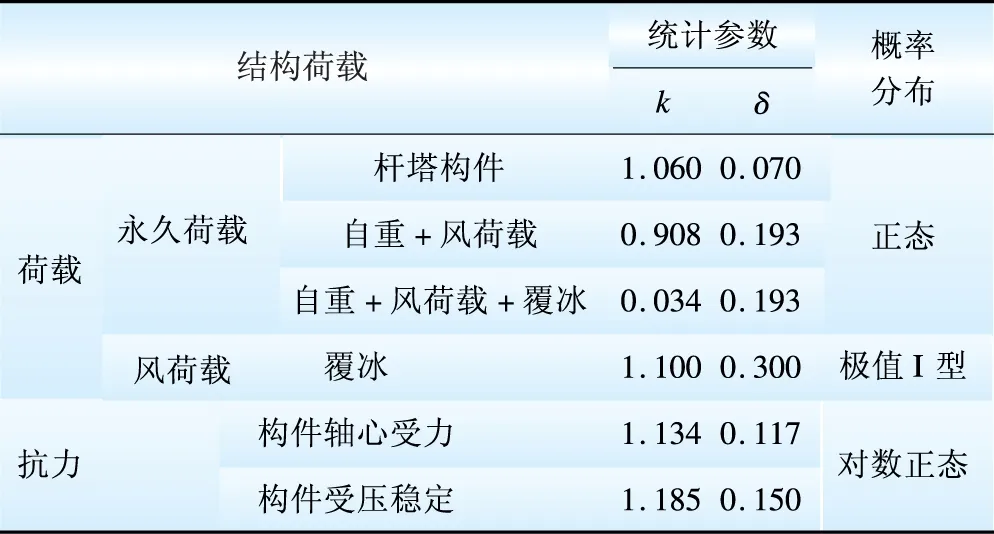
表4 荷載、桿塔構件抗力的統計參數

2 可靠度校準

2.1 基本設計表達式

結構可靠度校準是計算結構或結構構件按規范設計表達式設計，剛好滿足規范要求時的可靠度，反映了設計規范的最低安全水平。我國標準GB 50545—2010《110 kV～750 kV架空輸電線路設計規范》[18]中采用的分項系數設計表達式為

(10)

式中：γ0為桿塔結構重要性系數，重要線路不小于1.1，臨時線路取0.9，其他線路取1.0；γG為永久荷載分項系數，對結構受力有利時不大于1.0，不利時取1.2；γQi為第i個可變荷載的分項系數，取1.4；SGk、SQik分別為永久荷載效應標準值、第i個可變荷載效應標準值；Rd為結構構件的抗力設計值，根據規范GB 50545—2010第8章，不同構件采用不同的抗力表達式；φ為可變荷載組合系數，正常運行情況取1.0，斷線情況、安裝情況和不均勻覆冰情況取0.9，驗算情況取0.75。

根據式(10)，滿足規范最低要求的抗力設計值為：

Rd=γ0(γGSGk+φ∑γQiSQik)

(11)

2.2 構件可靠指標計算

2.2.1 抗力計算

(1)構件軸心受力。

我國DL/T 5154—2002《架空送電線路桿塔結構設計技術規定》，構件軸心受力時的強度計算應滿足：

(12)

式中：An為構件凈截面面積；fd為鋼材的強度設計值；m為構件強度折減系數。

滿足規范最低要求的軸向力為

N=Rd=mAnfd

(13)

由式(11)和式(13)可得出：

(14)

式中：NGk和NQik分別為永久荷載和第i個可變荷載產生的軸向力標準值。

(2)構件受壓穩定。

同樣，根據標準DL/T 5154—2002的規定，構件軸心受壓穩定的計算應滿足：

(15)

式中：φk為鐵塔構件軸心受壓時的穩定系數，按DL/T 5154—2002確定。

由式(14)和式(15)得：

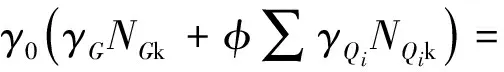
(16)

2.2.2 可靠指標計算

考慮永久荷載與風荷載組合及永久荷載與風荷載和覆冰荷載組合2種情況。構件軸心受壓穩定時的分析除抗力統計參數與軸心受力構件不同外，功能函數、荷載和抗力的平均值和標準差與構件軸心受力的表達方式均相同，下面以構件軸心受力的情況為例說明可靠指標的計算過程。

(1)永久荷載與風荷載組合。

可靠度計算時將設計中的變量視為隨機變量，構件軸心受力時的功能函數為

Z=R-NG-NW

(17)

式中：R為構件抗力；NG為永久荷載產生的軸力；NW為風荷載產生的軸力。

永久荷載和風荷載的平均值和標準差分別為：

(18)

(19)

抗力的平均值為

(20)

式中：kR為抗力的均值系數，如表4所示。

不同品種和厚度鋼材強度的標準值和設計值如表5所示。

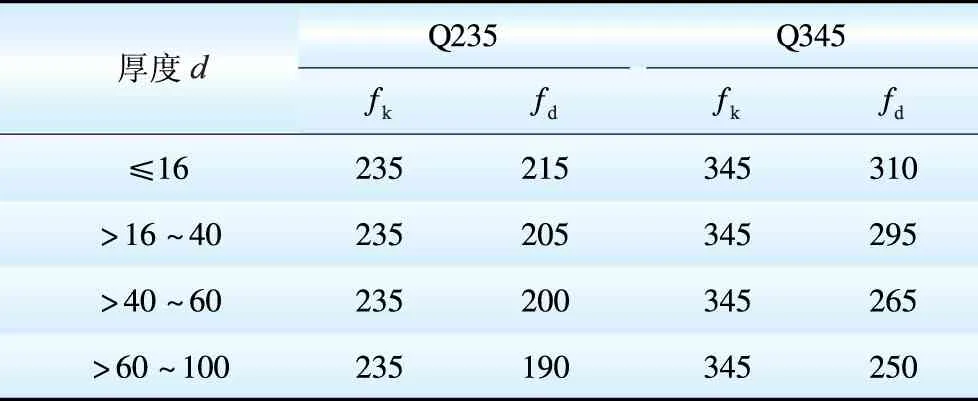
表5 鋼材強度的標準值和設計值

作用在桿塔上的風荷載包括風吹動桿塔構件產生的風荷載和風吹動絕緣子、金具和導地線產生的風荷載。規范GB 50545—2010《110 kV～750 kV架空輸電線路設計規范》規定，在計算作用于500 kV和750 kV的桿塔上導地線的風荷載時(不包括導地線張力弧垂計算和風偏角計算)，還需考慮表6中的風荷載調整系數βc。根據設計經驗，風吹動絕緣子、金具和導地線產生的風荷載一般為總風荷載的一半，將式(14)代入式(20)得：

(21)

式中γQ1為風荷載的分項系數。

表6 風荷載調整系數βc

由式(18)、式(19)和式(21)可以看出，結構抗力、永久荷載效應和風荷載效應的平均值和標準差均與永久荷載標準值NGk成正比，因此，計算可靠指標時，無需涉及荷載效應和抗力的具體值，僅與風荷載效應比ρW的取值有關。

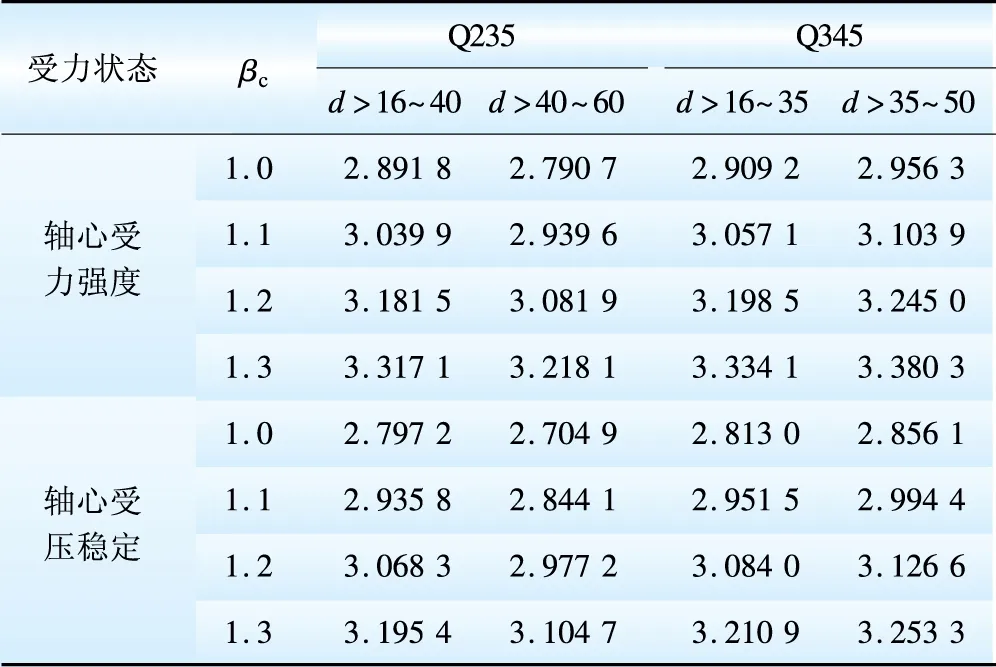
根據多個實際輸電塔的分析，取ρW=0.1～100。當永久荷載與風荷載組合時，采用JC方法計算得到的不同風荷載調整系數時不同鋼號桿塔構件可靠指標隨ρW的變化趨勢，如圖2和圖3所示，不同鋼號和風載調整系數時的平均可靠指標見表7。

由圖2和圖3可以看出，桿塔構件可靠指標與荷載比值ρW有關。荷載比值ρW≤1.0時，構件軸心受力強度的可靠指標隨ρW的增加而增大；而ρW>1.0時，構件軸心受力強度的可靠指標隨ρW的增大而減小。由表7可知，構件平均可靠指標隨著風荷載調整系數βc的增大而增大，構件軸心受壓穩定的可靠指標小于軸心受力強度的可靠指標。

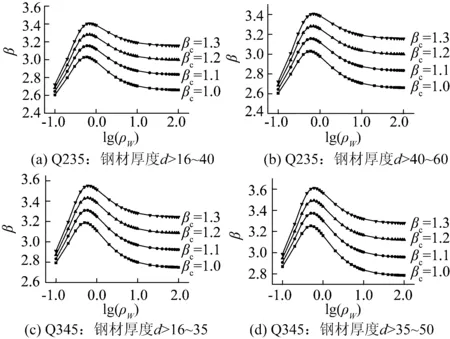
圖2 構件軸心受力強度的可靠指標(永久荷載+風荷載)

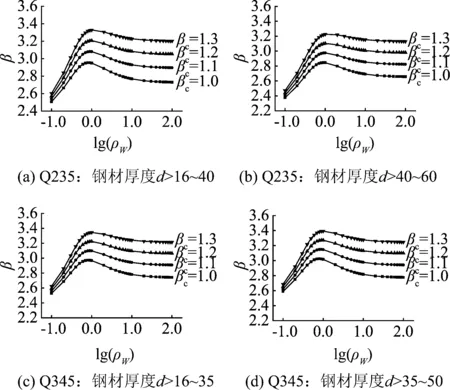
圖3 軸心受壓穩定的可靠指標(永久荷載+風荷載)

表7不同鋼號構件的平均可靠指標(永久荷載+風荷載)

Tab.7Reliabilityindexesofmembersofdifferentsteelgrades(deadload+windload)

(2)永久荷載、風荷載和覆冰荷載組合。

仍以構件軸心受力強度的情況說明。永久荷載、風荷載和覆冰荷載組合時，構件軸心受力強度的功能函數為：

Z=R-NG-NW-NI

(22)

那么，覆冰組合下風荷載效應和覆冰荷載效應的平均值和標準差為：

(23)

(24)

式中：kNWI，δNWI，kNI，δNI分別為覆冰組合下風荷載和覆冰荷載的均值系數和變異系數。

構件軸心受壓強度抗力的平均值為

(25)

式中γQ2分別為覆冰荷載的分項系數。

對于永久荷載+風荷載+覆冰荷載組合，覆冰荷載起控制作用。根據對實際輸電桿塔的計算分析，覆冰荷載與永久荷載標準值產生的軸力之比ρI可取0.02～5，覆冰工況下風荷載與永久荷載標準值產生的軸力之比ρWI可取0.02～10。采用JC法計算的桿塔構件不同鋼號軸心受力強度和軸心受壓穩定的可靠指標隨ρI和ρWI的變化趨勢如圖4和圖5所示，每種情況下的平均可靠指標如表8所示。

由圖4和圖5可看出，在永久荷載+風荷載+覆冰荷載的組合下，ρI一定時，不同ρWI對應的可靠指標隨ρWI的增大而增大；ρWI一定時，可靠指標隨著ρI的增大而降低。從表8可以看出，構件軸心受壓穩定的可靠指標也小于軸心受力強度的可靠指標。

圖4 構件軸心受力強度的可靠指標

圖5 構件軸心受壓穩定的可靠指標

文獻[19]對國家標準GB 50010—2001《鋼結構設計規范》的可靠度進行了校準，永久荷載與風荷載組合時的可靠指標為2.94，小于永久荷載與樓面活荷載組合時的可靠指標。在2006年瑞典斯德哥爾摩召開的第9屆概率方法在電力系統應用國際會議上，文獻[8]發表了對NESC C2—2002《美國國家電力安全規范》的可靠度校準結果，永久荷載與風荷載組合的可靠指標為2.36～3.01，永久荷載與風荷載和覆冰組合時桿塔構件的可靠指標為2.29～3.91；對加拿大標準CSA C22.3 No.1—2001《高架線路系統》的可靠度校準結果為，桿塔構件永久荷載與風荷載組合時的可靠指標為0.85～2.00，永久荷載與風荷載和覆冰組合時的可靠指標為1.68～2.78。

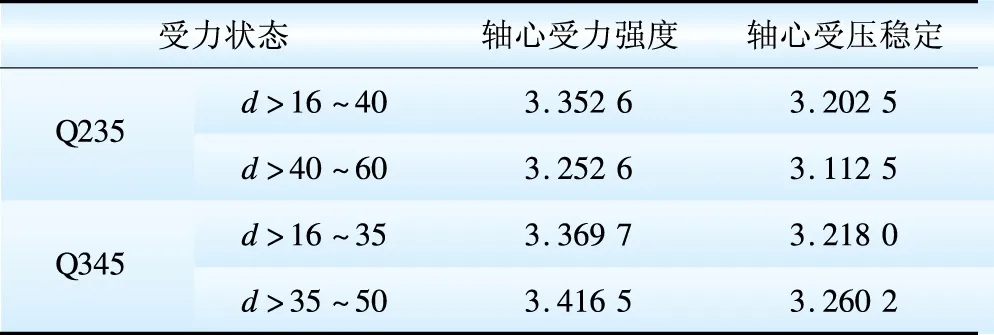
表8 不同鋼號桿塔構件的可靠指標(永久荷載+風荷載+覆冰荷載)

由此可見，永久荷載與風荷載組合時我國輸電線路桿塔桿件的可靠度水平比建筑鋼結構的可靠度略低，與美國桿塔構件的可靠度水平相近，比加拿大桿塔構件的高；永久荷載、風荷載與覆冰組合時我國輸電線路桿塔桿件的可靠度水平與美國桿塔構件的可靠度水平相近，比加拿大桿塔構件的高。

3 結 論

本文對按現行國家標準GB 50545—2010和行業標準DL/T 5154—2002規定設計的角鋼桿塔進行了可靠度校準，明確了我國角鋼桿塔構件的可靠度水平。分析得出如下結論：

(1)在永久荷載與風荷載組合下，構件軸心受力強度的可靠指標平均約為3.102 8，構件軸心受壓穩定的可靠指標平均約為2.994 9；在永久荷載與風荷載和覆冰荷載的組合下，構件軸心受力強度的可靠指標平均約為3.347 9，構件軸心受壓穩定的可靠指標平均約為3.198 3；

(2)永久荷載與風荷載組合時我國輸電線路桿塔桿件的可靠度水平比建筑鋼結構的可靠度略低。永久荷載與風荷載組合及永久荷載、風荷載與覆冰組合時，我國輸電線路桿塔桿件的可靠度水平與美國桿塔構件的可靠度水平相近，比加拿大桿塔構件的高。

[1]梁德飛. 輸電線路大跨越鋼管塔的結構可靠度分析[J]. 武漢大學學報：工學版，2009，42(增刊)：249-252.

[2]李峰，袁駿，侯建國，等. 我國輸電線路鐵塔結構設計可靠度研究[J]. 電力建設，2010，31(11)：18-23.

[3]李茂華，李正，楊靖波，等. 特高壓輸電線路桿塔可靠度研究[J]. 電網技術，2010，34(5)：21-24.

[4]馮徑軍，柳春光，馮嬌. 輸電塔線在覆冰與風載下的可靠性分析[J]. 水電能源科學，2011，29(10)：203-206.

[5]秦力，張學禮，張杰，等. 淺析500 kV輸電鐵塔結構體系的可靠性[J]. 東北電力大學學報，2008，28(2)：9-12.

[6]侯建國，徐彬，董黛，等. 國內外架空輸電線路設計規范安全度設置水平的比較[J]. 武漢大學學報：工學版，2011，44(增刊)：262-171.

[7]Haarlaa L, Pulkkinenb U, Koskinenc M, et al. A method for analysing the reliability of a transmission grid [J]. Reliability Engineering and System Safety, 2008, 93(2): 277-287.

[8]Guori B, Hong L. Achieved reliability of the North American design approaches for transmission overhead structures[C]//9th International Conference on Probabilistic Methods Applied to Power Systems, KTH, Stockholm, Sweden, 2006: 11-15.

[9]NESC C2—2002. National electrical safety code[S]. Institute of Electrical & Electronics Engineers, 2002.

[10]ASCE 74—2009. Guidelines for electrical transmission line structural loading[S]. American Society of Civil Engineers, 2009.

[11]CAN-CSA22.3 No.1. Canadian electrical code：overhead systems[S]. Canadian Standards Association, 2001.

[12]EN 50341-1. Overhead electrical lines exceeding AC 45 kV[S]. European Committee for Electrotechnical Standardization, 2001.

[13]IEC 60826—2003. Design criteria of overhead transmission lines[S]. International Electrotechnical Commission, 2003.

[14]貢金鑫，魏巍巍. 工程結構可靠性設計原理[M]. 北京：機械工業出版社，2007.

[15]蔣興良，易輝. 輸電線路覆冰及防護[M]. 北京：中國電力出版社，2002.

[16]黃興棣. 工程機構可靠性設計[M]. 北京：人民交通出版社，1992.

[17]DL/T 5154—2002 架空送電線路桿塔結構設計技術規定[S]. 北京：中國電力出版社，2002.

[18]中國電力企業聯合會. GB 50545-2010 110 kV～750 kV架空輸電線路設計規范[S]. 北京：中國計劃出版協會，2010.

[19]戴國欣，劉海鑫. 新鋼結構設計規范總體安全度分析[J]. 建筑科學，2002,18(增刊)：73-75.

(編輯：張媛媛)

ReliabilityCalibrationofTowerMembersinTransmissionLine

FENG Yunfen1, GONG Jinxin1, LI Hongnan1, ZHANG Ziyin2

(1. Faculty of Infrastructure Engineering Dalian University of Technology, Dalian 116024, Liaoning Province, China;2.State Power Economic Research Institute, Beijing 102209, China)

To set the reliability level of transmission line crossing high speed railway, the statistical parameters of the load and resistance of tower members in transmission line were analyzed and calculated. The reliability of tower members designed based on the current code were calibrated. It is indicated that the reliability indexes for strength of axially loaded members or the stability of axial compression members are 3.10 and 2.99, respectively, in the combination of permanent load and wind load; and are 3.35 and 3.20 respectively, in the combination of permanent load, wind load and ice load. The reliability of tower member in transmission lines in China is somewhat lower than that of building steel structures, in the combination of permanent load and wind load; but it is close to the reliability of tower members in US, and higher than that in Canada, in the combination of permanent load and wind load, or in the combination of permanent load, wind load and ice load.

transmission line; tower member; reliability; calibration

國家自然科學基金委創新研究群體基金項目(51121005)；國家電網公司科技項目(B3440912K006)；高等學校學科創新引智計劃資助項目(B08014)。

編者按

基于上述情況，本刊特邀國網北京經濟技術研究院、大連理工大學等單位總結了“國家電網公司科技項目：輸電線路跨越高鐵關鍵技術研究”的相關成果，推出了“跨越高鐵輸電線路可靠度研究”專欄。本期共刊登相關論文5篇，內容涉及輸電線路桿塔結構的可靠度校準、輸電線路絕緣子、金具和導地線的可靠度校準、跨越高速鐵路輸電線路的目標可靠指標等。希望此次專欄為從事輸電線路可靠度的科研工作人員提供一些參考和借鑒。本專欄得到了大連理工大學貢金鑫教授、李宏男教授以及國網北京經濟技術研究院張子引高工、田雷高工的大力支持，在此一并表示感謝！

TM 732

： A

： 1000-7229(2014)05-0013-08

10.3969/j.issn.1000-7229.2014.05.003

2013-11-07

：2014-02-18

馮云芬(1982)，女，博士，主要從事工程結構可靠度與結構耐久性方面的研究工作，E-mail：fengyunfen@126.com；

貢金鑫(1964)，男，博士，教授，博士生導師，主要從事工程結構可靠度、數值分析及鋼筋混凝土結構耐久性方面的研究工作，E-mail：gong_jx.vip@eyou.com；

李宏男(1958)，男，博士，長江學者特聘教授，博士生導師，主要從事大跨越輸電塔體系的抗震計算理論、結構減震控制、重大工程健康監測與損傷評估等方面的研究工作，E-mail：hnli@dlut.edu.cn；

張子引(1971)，男，本科，高級工程師，主要從事輸電線路設計技術研究及電網工程評審和咨詢工作，E-mail：zhangziyin@chinasperi.sgcc.com.cn。

隨著我國經濟的迅猛發展，對電力需求直線增長，輸電線路體系日趨大型化、復雜化；與此同時，我國高鐵的迅速發展使得輸電線路跨越高鐵的情況經常出現。為保證高鐵安全運行，對跨越高鐵輸電線路的可靠性提出了更高要求。由于輸電線路與鐵路基礎設施的設計方法不同，設計規范中材料強度的取值、分項系數或安全系數的含義不同，因此，需要建立一個統一的尺度分析跨越高鐵輸電線路的安全性。