歪斜安裝對組配軸承轉子系統動力學特性影響

易均,劉恒,劉意,景敏卿

(西安交通大學機械工程學院, 710049, 西安)

歪斜安裝對組配軸承轉子系統動力學特性影響

易均,劉恒,劉意,景敏卿

(西安交通大學機械工程學院, 710049, 西安)

針對多聯組配軸承歪斜安裝情況,推導了一個軸承外圈發生繞豎直方向歪斜時滾動軸承的非線性支承力形式,并借助Timoshenko梁軸單元建立了主軸模型,利用打靶法和Floquet理論分析了歪斜對系統全局非線性穩定特性和振動特性的影響。通過與正常安裝組配軸承轉子系統對比發現:外圈歪斜后系統在大間隙時的低轉速區域容易出現倍周期分叉,在高轉速區域易表現為偽周期分叉;在小間隙工況時容易獲得大范圍的周期運動參數區域。同時,歪斜使得系統的一臨界峰峰值右移且明顯放大,從而導致系統在高轉速區域的水平方向振動明顯增大。研究結果表明,掌握且合理利用軸承歪斜后的非均勻間隙特性,有助于改善系統運行的動力特性。

歪斜安裝;滾動軸承;多聯組配;間隙特性;穩定特性

組配軸承由2個或者多個角接觸軸承成對安裝而成,以獲得更高的支承精度和承載能力,并廣泛應用于機床、精密儀器、高速離心機等領域[1]。為了保障組配軸承轉子系統的穩定運行,除了對角接觸軸承本身動力特性提出嚴格要求外,更重要的是對組配軸承安裝技術提出了特殊要求。

目前,國內外早已對單列角接觸軸承展開了研究。Yamamoto在Jeffcott轉子中考察了軸承間隙的非線性動力影響[2]。Tiwari不僅在理論上考察了軸承內部間隙的非線性動力特性,還實驗驗證了非線性失穩現象[3-4]。Harsha在計入表面波紋度和徑向間隙等多種非線性因素的同時,利用龐加萊截面和頻譜結果分析了滾動軸承支承轉子的偽周期、倍周期和混沌等非線性動力特性[5]。袁茹結合阻尼特性和徑向間隙,考察了簡單Jeffcott轉子的非線性行為[6]。白長青建立了滾動軸承支承平衡轉子模型,結合Floquet理論研究了周期解失穩的3種途徑[7]。對于組配軸承安裝技術,Aini通過實驗詳細分析了多支承軸承的頻率特性,建立了角接觸軸承的五自由度簡化動力學模型[8]。Rahman借助Aini的五自由度模型,研究了多個滾動軸承支承主軸在不同安裝方式下的動力響應[9]。羅平利用Timoshenko梁軸單元建立了主軸模型,討論了組配軸承安裝過程中出現錯位時的非線性動力響應[10]。然而,以上研究并未對組配軸承安裝過程或使用過程中出現的外圈歪斜進行深入討論。

本文推導了組配軸承中一個軸承外圈發生繞豎直方向歪斜時軸承的非線性支承力表達形式。借助Timoshenko梁軸單元和赫茲接觸理論,建立了組配軸承轉子系統模型,并利用打靶法和Floquet理論進行方程求解和失穩判別。研究時將軸承內部間隙和工作轉速共同構成動力響應的討論域,以期獲得軸承內部間隙連續變化時系統動力響應,以及軸承外圈歪斜時系統的振動特性。

1 系統建模

圖1 組配軸承主軸示意圖

圖2 主軸有限元模型單元

組配軸承主軸系統如圖1所示。該系統主要由線性轉軸、非線性支承軸承及不平衡輪盤組成。主軸采用Timoshenko有限元單元進行離散,如圖2所示,并利用哈密頓原理進行系統組裝。系統動力學方程為

(1)

式中:M、G、K分別為系統的質量矩陣、陀螺矩陣和剛度矩陣;Fb為非線性支承力向量;Fu為輪盤不平衡周期激勵;Fg為系統重力向量;q為系統節點自由度。

2 滾動軸承非線性軸承力

假設滾動軸承的滾子均勻分布于內、外滾道之間,如圖3所示。角接觸球軸承受力后在滾動體與內、外滾道之間發生接觸變形,軸承接觸力與接觸變形之間的關系可用赫茲公式計算。根據赫茲彈性接觸理論,第j個滾動體與內、外滾道間的接觸力Qj及彈性變形量δj可表示為

(2)

式中:kj表示第j個滾動體與內、外滾道間的總等效剛度系數[11]。圖3所示的滾動軸承坐標系中第j個滾動體在t時刻的轉角為

(3)

式中:Nb表示滾動體個數;ωc表示滾動體公轉轉速。本文中假設軸承外滾道不隨轉軸一起轉動,內滾道與轉軸一起旋轉。

ω:轉軸轉速;VA、VB:滾動體內、外圈接觸點線速度;VC:滾動體公轉線速度;r、R:軸承內、外圈滾道半徑;α:接觸角

根據圖3模型,滾動體公轉速度

(4)

對于正常安裝無歪斜的滾動軸承,在計入初始間隙γ后的彈性變形量

δj=(xcosθj+ysinθj)cosα-γ

(5)

式中:x和y表示內滾道水平和豎直位移。

L:t時刻正常情況滾子在外滾道的接觸點位置;L′:t時刻歪斜后滾子在外滾道的接觸點位置;φ:軸承外滾道繞y軸歪斜的角度

組配中軸承安裝歪斜后的示意如圖4所示。歪斜后第j個滾子與內、外滾道間由于歪斜而引起的徑向間隙改變量

γj=R-((Rcosθjcosφ)2+(Rsinθj)2)1/2

(6)

因此,歪斜安裝時軸承的徑向間隙

γej=γ-γj

(7)

歪斜安裝后第j個滾子與滾道間的接觸變形

δej=(xcosθj+ysinθj)cosα-γej

(8)

利用赫茲接觸理論,第j個滾子與內、外滾道間的接觸力

(9)

根據式(2),同時考慮軸承的阻尼效應,可得整個軸承的非線性支承力在x和y方向的分量,即

(10)

式中:cb為接觸阻尼。根據文獻[12]查得cb和等效剛度之間的關系為

cb=1.0×10-5kj(δθj)1/2

(11)

經計算kj=1.0831×1010N/m3/2。本文軸承參數參見文獻[10]。

3 數值模擬結果與討論

如圖5所示,用2個非線性彈簧模擬多聯組配軸承,其彈性力為軸承非線性力。轉子的結構參數如下:軸直徑為80mm,軸長度為550mm,圓盤寬度為80mm,圓盤直徑為120mm,材料密度為7 800kg/m3,彈性模量為2.103×1011N/m2,泊松比為0.3。將圖1轉子系統均勻離散為11個單元和12個節點,每個節點有4個自由度,節點2、11、12處為滾動軸承支承(節點11處的軸承在安裝時繞豎直方向發生歪斜),節點5、8處為輪盤位置,系統不平衡質量為輪盤的偏心質量,質量偏心作用于oxy平面。當在x、y方向的質量偏心為8 μm時,本文采用打靶法及追蹤算法研究了非線性動力系統穩態周期解隨外參數(轉速)變化的穩定性分岔規律,詳見文獻[10]。

1～11:轉子系統均勻離散后的單元節點數

3.1 徑向間隙對全局特性的影響

實際中,工況波動和摩擦生熱等因素會導致徑向間隙在連續大范圍內波動,因此滾動軸承轉子系統的全局動特性研究域由徑向間隙與轉速共同構成,如圖6所示。該研究域橫坐標為工作轉速,縱坐標為徑向間隙,動力穩定性采用如下符號表示:T1、T2表示周期解區域;D1、D2分別表示2倍周期解、4倍周期解區域;Q1、Q2、Q3表示偽周期解區域。從圖6中可以看出:當γ<3時,25000r/min以下系統能在較大范圍獲得穩定周期解區域,而在高轉速區域表現出偽周期運動特性;當γ=3時,偽周期區域Q1突然出現,并隨著轉速的升高先后出現了D2、D1及Q2等失穩區域,充分表明徑向間隙對系統具有強非線性影響,同時也對此類軸系設計提出了全局動力響應考察的技術要求。γ=3時系統在不同區域的動態響應如圖7所示。γ>5時,高轉速區域的偽周期區域Q2突然消失,系統進入大參數范圍的穩定工況區域T2。Q1和D2分別在γ=5和γ=7時發生且逐漸消失,D1在γ=10時消失,此時系統進入大參數范圍的非線性動力響應的穩態區域T2。

圖6 正常安裝軸系全局穩定性示意圖

(a)位移分叉圖

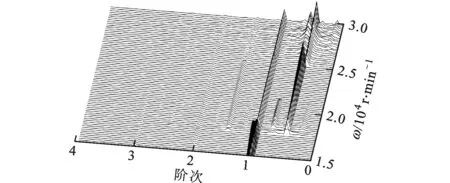
(b)頻譜轉速圖

(c)不同轉速下輪盤位置軸心軌跡圖

3.2 軸承外滾道歪斜對全局動力特性的影響

軸承外滾道繞豎直方向發生一定程度的歪斜,相當于以外滾道豎直方向端點沿周向到水平方向端點的徑向間隙逐漸減小(見式(8)),甚至在水平位置形成負間隙。因此,從動力特性上看,歪斜是對系統水平方向的約束,并產生一個極小的繞y軸的附加力矩。由此,本文從動力學角度出發,探討了軸承外滾道歪斜后的非線性動力特性(忽略溫升因素)。實際中,間隙的設置通常是為了抵消軸承熱膨脹,防止軸承抱死。雖然外滾道歪斜后系統的水平方向約束得以加強,但是間隙由于非設計因素而減小,所以軸

承溫升加劇。

外滾道在不同程度歪斜時系統全局動力特性如圖8所示。從圖8可以看出,隨著軸承外滾道繞y軸歪斜的角度φ的增大,系統在小間隙范圍內獲得的穩定周期解區域增大,以D1為代表的失穩區域出現時要求γ增大,本文坐標系中表現為整體上移,同時Q1和D2隨著φ的增大而逐漸消失。在高轉速區域,Q2表現出整體上移,并在小間隙時出現一個新的倍周期區域D3。從圖8還可以看出:當系統的軸承間隙較大時,受φ的影響,系統極有可能發生倍周期或者偽周期失穩;當系統的軸承間隙較小時,φ反而容易使系統穩定的周期運動區域擴大。但是,需要指出,外滾道歪斜很可能使得小間隙系統變為負間隙,軸承溫升將明顯加劇。

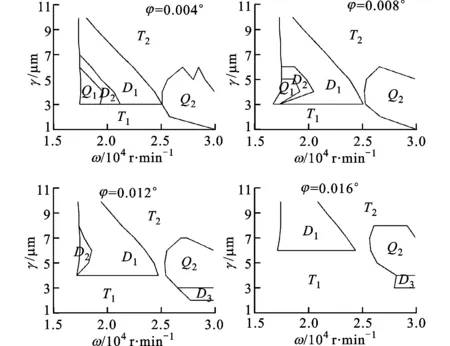
圖8 外滾道在不同程度歪斜時系統全局動力特性

3.3 軸承外滾道歪斜對系統振動特性的影響

對于機床主軸來說,除了動力穩定性外,振動幅值也是影響加工工件質量的關鍵因素。振動量過大必然導致加工質量下降,因此有必要對歪斜軸系的振動規律進行探討。為了排除間隙引起非線性失穩的影響,置徑向間隙γ=1,輪盤不平衡量為1 μm,結果如圖9所示。從圖9可以看出,φ使得系統在x方向的振動峰明顯右移且峰值增加了146%,而在y方向的振動峰稍微左移且略有減小。可見,在一臨界前,系統歪斜后振動較小,在一臨界后,x方向上振動明顯增大。從圖9還可以看出:歪斜后系統振動峰值減小,同時豎直方向上軸心位置變形減小,表明外滾道歪斜后約束加強,軸的擾度減小;在一臨界后,x方向上的系統振幅遠大于正常安裝系統,而y方向上變化不大。

圖9 外滾道在不同程度歪斜時的系統振動特性

4 結 論

本文建立了組配軸承支承主軸動力學模型,推導了軸承外滾道繞豎直方向歪斜時軸承非線性力表達式,并借助打靶法和Floquet理論進行了穩態響應求解和失穩判別,繪制了軸承徑向間隙-工作轉速工況參數圖,討論了軸承間隙和外滾道歪斜對組配軸承支承系統的全局非線性動力特性的影響規律。

仿真結果表明,對于正常安裝的主軸系統,偽周期分叉和倍周期分叉為系統主要失穩形式。軸承外滾道發生歪斜時,隨著歪斜量增大,大間隙工況系統易發生倍周期失穩和偽周期失穩,而小間隙工況的非線性穩定性可以得到改善。同時,隨著歪斜量的增大,系統在水平方向上一臨界振動峰明顯右移且峰值增大,而在豎直方向上的變化較小,所以系統在高速區域時水平方向的振動明顯增大。

[1] GAO S H, MENG G, LI H G, et al. Non-linear dynamics of an unbalanced machine-tool spindle system supported by ball bearings [J]. Proceedings of the Institution of Mechanical Engineers: Part K Journal of Multi-Body Dynamics, 2008, 222(3): 201-214.

[2] YAMAMOTO T. On the vibration of a shaft supported by bearings having radial clearances [J]. Transactions of the JSME, 1955, 21(103): 182-192.

[3] TIWARI M, GUPTA K, PRAKASH O. Effect of

radial internal clearance of a ball, bearing on the dynamics of a balanced horizontal rotor [J]. Journal of Sound and Vibration, 2000, 238(5): 723-756.

[4] TIWARI M, GUPTA K, PRAKASH O. Dynamic response of an unbalanced rotor supported on ball bearings [J]. Journal of Sound and Vibration, 2000, 238(5): 757-779.

[5] HARSHA S P, SANDEEP K, PRAKASH R. Non-linear dynamic behaviors of rolling element bearings due to surface waviness [J]. Journal of Sound and Vibration, 2004, 272(3/4/5): 557-580.

[6] 袁茹, 趙凌燕, 王三民. 滾動軸承-轉子系統的非線性動力學特性分析 [J]. 機械科學與技術, 2004, 23(10): 1175-1177.

YUAN Ru, ZHAO Lingyan, WANG Sanmin. Analysis of the nonlinear dynamic behaviors of a rolling bearing-rotor system [J]. Mechanical Science and Technology, 2004, 23(10): 1175-1177.

[7] 白長青, 許慶余, 張小龍. 考慮徑向間隙的滾動軸承平衡轉子系統的非線性動力穩定性 [J]. 應用數學與力學, 2006, 27(2): 159-169.

BAI Changqing, XU Qingyu, ZHANG Xiaolong. Nonlinear stability of balanced rotor due to the effect of ball bearing internal clearance [J]. Applied Mathematics and Mechanics, 2006, 27(2): 159-169.

[8] AINI R, RAHNEJAT H, GOHAR R. A 5degrees of freedom analysis of vibrations in precision spindles [J]. International Journal of Machine Tools & Manufacture, 1990, 30(1): 1-18.

[9] RAHMAN A K, AINI R, GOHAR R. On the performance of multi-support spindle-bearing assemblies [J]. Proceedings of the Institution of Mechanical Engineers: Part K Journal of Multi-Body Dynamics, 2002, 216(2): 117-32.

[10]羅平, 劉恒, 景敏卿. 錯位安裝對多聯組配軸承轉子系統動力學特性的影響 [J]. 西安交通大學學報, 2011, 45(7): 106-111.

LUO Ping, LIU Heng, JING Minqing. Influence of misdisplacement on dynamic characteristics system of rotor supported by combined ball bearings [J]. Journal of Xi’an Jiaotong University, 2011, 45(7): 106-111.

[11]HARRIS T A. Rolling bearing analysis [M]. New York, USA: John Wiley & Sons, 1984: 160-162.

[12]KRAMER E. Dynamics of rotors and foundations [M]. Berlin, Germany: Springer, 1993: 140-141.

(編輯 苗凌)

InfluenceofInstalledOuterRaceonNonlinearDynamicCharacteristicsforMatchedBearings-RotorSystem

YI Jun,LIU Heng,LIU Yi,JING Minqing

(School of Mechanical Engineering, Xi’an Jiaotong University, Xi’an 710049, China)

For a skewing installed matched bearings-rotor system, an expression of the nonlinear supporting force is deduced when the outer race skews around the vertical axis. Timoshenke elements are chosen to model the flexible rotor, and shooting method is used to analyze the global nonlinear dynamic stability and vibration characteristics following Floquet theory. Compared with the normally installed bearing rotor system, the skewing with large internal clearance usually leads to multi-periodic behaviors in low speed region, and quasi-periodic behaviors in high speed region; the stable parameter region is widened for small clearance. The skewing makes vibration peak obviously right shift and magnified, and violent vibration then occurs horizontally in high speed region.

skewing installation; rolling bearing; matched bearings; clearance; stability

2013-12-31。

易均(1986—),男,博士生;劉恒(通信作者),男,教授。

國家自然科學基金資助項目(51175410);河南煤化基礎重大科研資助項目(2011LYC01-01)。

時間:2014-06-23

10.7652/xjtuxb201409018

TH113

:A

:0253-098X(2014)09-0107-05

網絡出版地址:http:∥www.cnki.net/kcms/detail/61.1069.T.20140623.1126.001.html