基于定子電流的MRAS轉速估計方案

張笠君， 阮 毅， 吳曉新， 柳 巍

(上海大學 機電工程與自動化學院，上海 200072)

0 引 言

無速度傳感器矢量控制需要準確估算轉速和磁鏈信息。目前，應用較廣的有模型參考自適應系統(Model Reference Adaptive System，MRAS)、Kalman濾波、人工神經網絡等[1-2]。基于MRAS的轉速估算發展到現在可以分成：(1)基于轉子磁鏈誤差的MRAS轉速估算方案，也是目前最常用的一種MRAS轉速估算方案，稱為傳統MRAS轉速估算[2-3]；(2)基于反電動勢的MRAS轉速估算方案，將計算的反電動勢和測量的反電動勢的誤差進行比較，得到轉速誤差[4]；(3)基于定子電流誤差的MARS轉速估算方案。通過定子電流模型計算出定子電流，與測量的定子電流進行比較，得到轉速誤差信號[5]。

文獻[2-3]將電壓模型作為參考模型，電流模型作為可調模型，為傳統的MRAS轉速估算方案。該方案結構并不復雜 、計算較簡單，但是電壓模型中存在純積分環節，會產生積分誤差和飽和，影響轉子磁鏈輸出。文獻[3]提出了一種改進方法，用高通濾波器替換純積分環節，再補償一個轉子磁鏈誤差，可以抑制積分漂移。文獻[4]是基于反電動勢的MRAS轉速估算方案。該方案提高了系統的魯棒性，但是同樣使用電壓模型作為參考模型，在計算轉子磁鏈時，由于定子電阻壓降作用明顯，測量誤差淹沒了反電動勢，使得觀測精度較低。

本文在基于傳統MRAS的基礎上，將參考模型改為感應電機本身，即通過感應電機的定子電流構造轉速辨識模型。這種方法對電機參數依賴比較小、動態響應快，不含純積分環節。通過MATLAB/Simulink對傳統MRAS轉速估算方案和本方案進行仿真。比較結果表明，本文介紹的這種方法具有較高的轉速辨識精度和動態響應。

1 傳統MRAS轉速估算方案

傳統的模型參考自適應是將電壓模型作為參考模型，電流模型作為可調模型，在電流模型中有轉速信號，通過自適應律使可調模型與參考模型的輸出宏偏差盡可能小，使計算的轉速盡可能接近于實際的轉速[5-6]。傳統的MRAS原理如圖1所示。

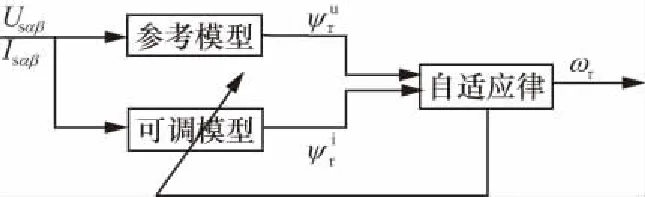
圖1 傳統MRAS原理圖

電壓模型方程為[2]

(1)

電流模型方程為[2]

(2)

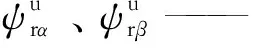
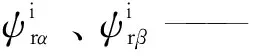
Lr——轉子電感；

Lm——互感；

Ls——定子電感；

usα、usβ——兩相定子電壓；

isα、isβ——兩相定子電流；

Rs——定子電阻；

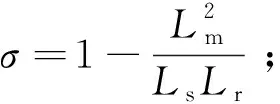
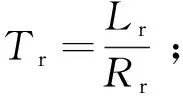
ωr——轉子角頻率。

根據Popov 超穩定理論，按MRAS 參數的結構，速度估算子模塊將估算轉速取為比例積分形式。自適應律為

(3)

2 基于定子電流的轉速估算方案

由式(1)可知，電壓模型并不是一個最理想的參考模型，尤其是在低速的時候，定子電阻壓降不可忽略，造成轉速估算不準確。

因此提出了基于定子電流的MRAS轉速估算方案。該方案是將電機本身作為參考模型，通過測量的電機實際電流與通過定子電流模型計算得出的電流偏差εis，經過自適應律調節，使偏差εis盡可能小，即計算出的電流與測得的電流盡可能接近，轉速就盡可能接近于實際轉速。沒有純積分環節，轉子磁鏈計算不需要定子電阻參數，因此在中低速時辨識精度也較高。

根據異步電機在α、β坐標系中的狀態方程得定子電流計算式[7]：

(4)

估算電流為

(5)

將實際定子電流減去估算電流得電流誤差為

(6)

(7)

由式(7)得

(8)

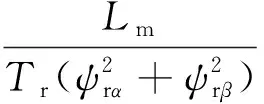
(9)

由式(2)、式(6)、式(9)得到基于定子電流的MRAS轉速估算原理圖如圖2所示。

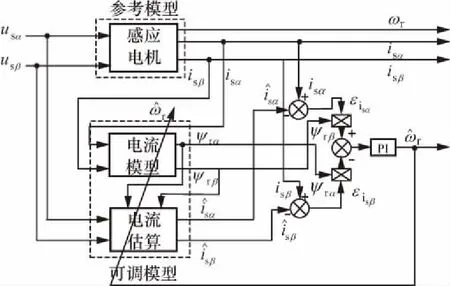
圖2 基于定子電流的MRAS轉速估計原理圖

3 基于定子電流的MRAS轉速估算矢量控制模型

速度反饋信號由MRAS速度辨識模塊輸出，采用電氣系統模塊庫和Simulink模塊可以建立仿真模型，其系統框圖如圖3所示。

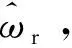
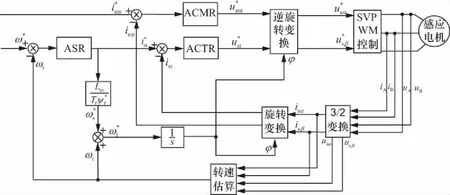
圖3 基于定子電流的MRAS轉速估算矢量控制系統框圖

4 與傳統方案仿真結果比較及分析

為驗證上述速度估算法的正確性及可行性，在MATLAB /Simulink 下建立了無傳感器矢量控制仿真系統，并進行仿真。同時與傳統的MRAS轉速估算方案進行比較。仿真采用的異步電機額定參數：PN=3 kW、fN=50Hz、np=2、UN=380 V、Rs=2.22 Ω、Rr=3.108 Ω、Lm=0.232 4 H、Ls=Lr=0.008 3 H、J=0.142 5 kg·m2。

仿真時空載起動，在系統運行到t=1 s時，突加一個階躍負載轉矩，大小為10 N·m。加載響應仿真結果如圖4所示。圖4(a)為轉速波形，圖4(b)為轉矩波形，圖4(c)為實際轉速與估算轉速誤差波形。

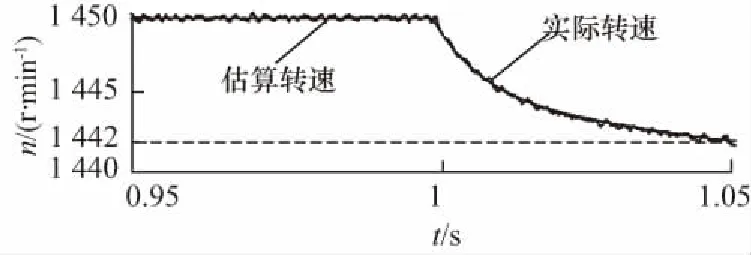
(a) 轉速波形

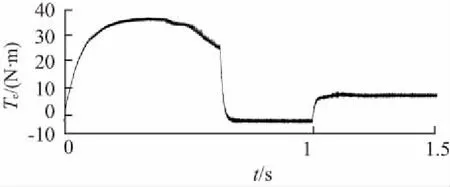
(b) 轉矩波形

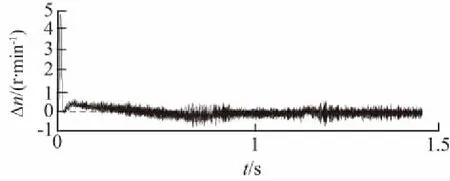
(c) 實際轉速與估算轉速誤差圖4 加載響應仿真結果

由圖4可知，給定轉速為1 450 r/min，加載之后，實際轉速下降至1 442 r/min，偏差εn=0.5%，略微下降，實際轉速與估算轉速誤差為Δn=1.2 r/min。說明系統在加載之后還能夠保持穩定。

兩種方案的動態響應如圖5所示。電機從給定轉速1 200 r/min起動，1 s之后給定突加到1 450 r/min的動態響應曲線。

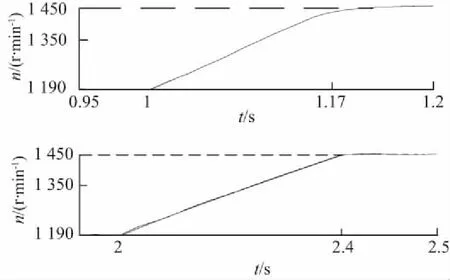
(a) 轉速波形

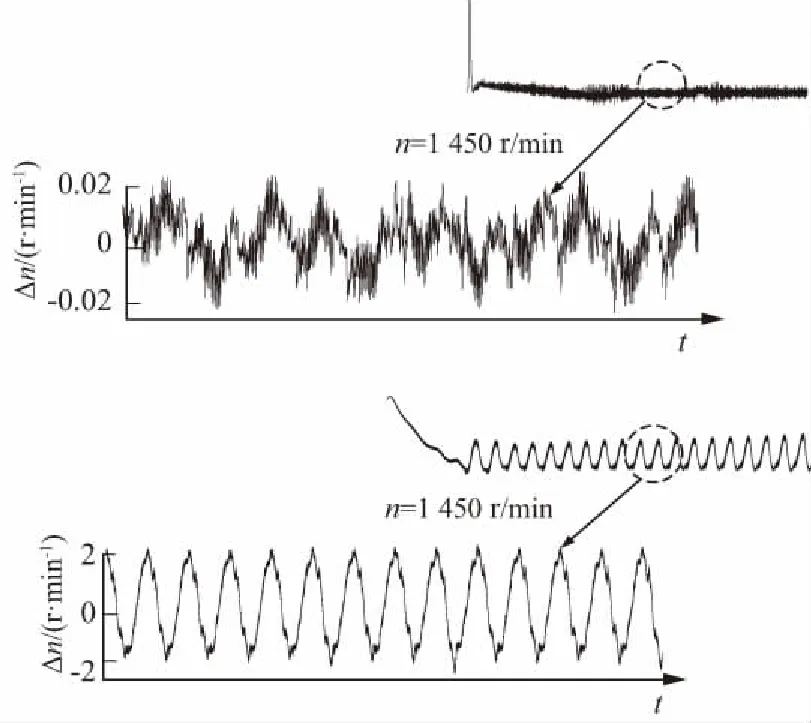
(b) 實際轉速與估計轉速誤差圖5 動態響應

圖5(a)是基于定子電流的MRAS轉速估算仿真圖。圖5(b)是基于傳統的MRAS轉速估算仿真圖。定子電流MRAS轉速從1 200 r/min上升到1 450 r/min，所用時間為0.17 s，穩態誤差Δn=0.04 r/min；傳統MRAS上升時間為0.4 s，穩態誤差Δn=4 r/min。從上述數據可以看出，高速時兩種估算方法的誤差都不是很大，但本文介紹的方法誤差更小，響應更快。

轉速200 r/min時，兩種方案的仿真結果如圖6所示。

從圖6可看出，在轉速為200 r/min的中低速階段，定子電流方案的實際轉速與估算轉速誤差Δn=3 r/min，而傳統方案的實際轉速與估算轉速誤差Δn=50 r/min，誤差很大，并且穩態時轉速不穩定。說明本文介紹的基于定子電流方案在中低速階段估算準確，誤差小，穩定性好。

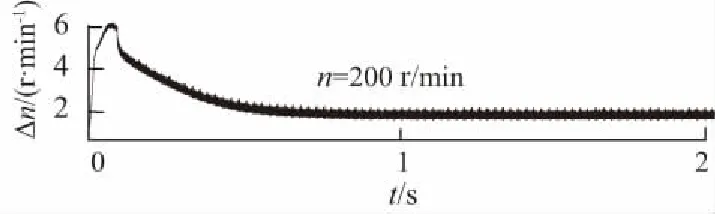
(a)定子電流方案實際轉速與估計轉速誤差

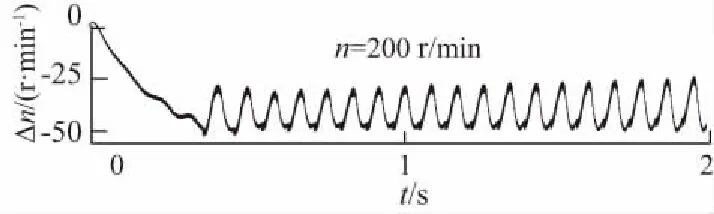
(b)傳統方案實際轉速與估計轉速誤差圖6 轉速為200 r/min時，兩種估算方案實際轉速與估算轉速誤差

5 結 語

本文根據定子電流和轉子磁鏈方程在兩相坐標系上推導出了異步電動機MRAS轉速辨識方法，利用電流偏差和磁鏈幅值進行轉速偏差的計算，系統魯棒性強，且結構簡單。仿真試驗結果表明系統速度估計準確、穩定性好、收斂速度快、對給定信號的跟蹤能力強，能夠滿足現代交流調速的高性能要求。

【參考文獻】

[1] KOWALSKA T O，DYBKOWSKI M． Stator-current-based MRAS estimator for a wide range speed-sensorless induction-motor drive[J]．IEEE Trans Ind Electron，2010，57( 2) : 1296-1308．

[2] SCHAUDER C. Adaptive speed identification for vector control of induction motors without rotational transducers[J]. IEEE Trans Ind Appl, 1992，28(5):1054-1061.

[3] 陳名輝，阮毅，宗劍,等. 無速度傳感器在礦用電機車矢量控制系統中的應用[J]．電機與控制應用，2012,39(2)：17-20.

[4] PENG F Z, FUKAO T. Robust speed identification for speed-sensorless vector control of induction motors[J]. IEEE Trans Ind Appl, 1994,30(5):1234-1240.

[5] 祝龍記，王賓. 基于MRAS矢量控制系統的仿真研究[J]．電工技術學報，2005,20(1)：60-65.

[6] 張毅，阮毅，張毅鳴,等. 基于dsPIC6010 的牽引型變頻器控制系統設計[J]． 電機與控制應用，2009( 2) : 3-6．

[7] 劉福才，陳龍，韓會山. 基于定子電流的MRAS矢量控制系統轉速辨識[J]．控制工程，2007(7):189-191.