一類三階常微分方程的兩點邊值問題的正解

頓調霞，李永祥

(西北師范大學數學與統計學院，甘肅蘭州730070)

1 預備知識

三階微分方程有著深刻的力學與物理背景，可以利用它研究電磁波或者重力流等.近年來對各類三階微分方程邊值問題的研究十分活躍，多種非線性分析的工具與方法被應用于三階微分方程邊值問題的研究當中［1-14］，主要有基于微分不等式的方法、拓撲度方法、上下解方法與單調迭代技巧等.文獻［1］在非線性項滿足超線性或次線性增長的情況下，考察了問題

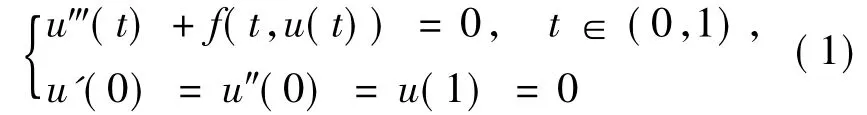
正解的存在性.文獻［2］利用 Krasnoselskii不動點定理討論了當非線性項f(t，u)可以在t=0，t=1及u=0處奇異時邊值問題(1)正解的存在性與多解性.文獻［3］應用上下解方法討論了三階兩點邊值問題

其中f:［0，1］×R→R連續，獲得了一些解的存在性結果.受上述文獻的啟發，本文利用Krasnoselskii不動點定理，在用不等式條件描述非線性項增長的條件下，研究三階常微分方程兩點邊值問題

正解的存在性，其中f:［0，1］×［0，∞)→［0，∞)連續.函數u*稱為問題(3)的正解，如果u*是(3)式的解，并且u*(t) ＞0，0 ＜t≤1.

2 預備工作

設C［0，1］為定義在［0，1］上的連續函數全體按范數構成的 Banach 空間.

引理 1［4］對?h∈C［0，1］，線性兩點邊值問題

引理2通過直接計算可得，由(6)式定義的函數G(t，s)具有下列性質

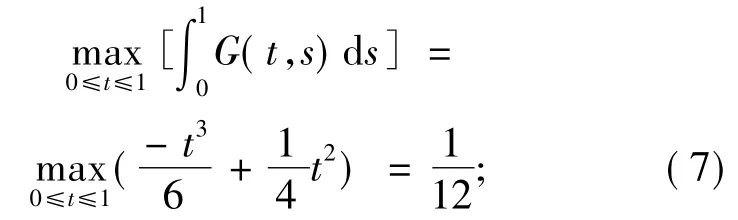
假設f:［0，1］×［0，∞ )→［0，∞ )連續，對?u∈C［0，1］，定義

則F:C［0，1］→C+［0，1］連續.這里C+［0，1］={u∈C［0，1］|u(t)≥0，t∈［0，1］}為C［0，1］中的正元錐.

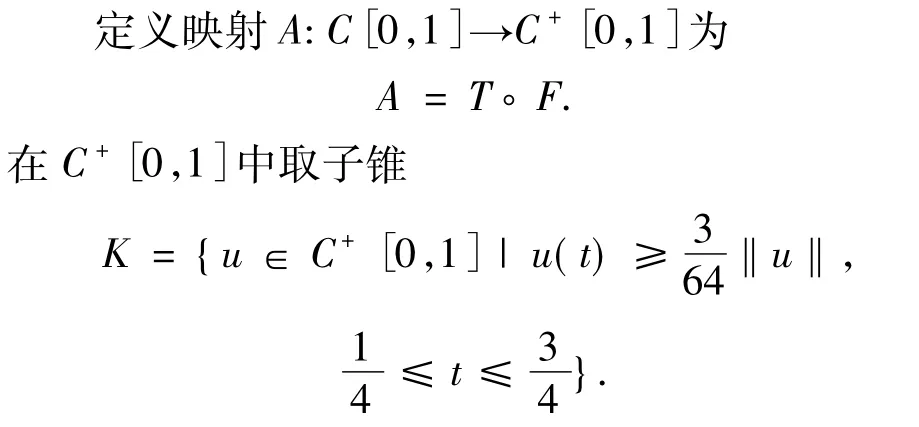
引理 3設f:［0，1］×［0，∞)→［0，∞)連續，則A(C［0，1］)?K且A:K→K全連續.

證明設u∈C［0，1］，對，根據(8)式有

因此Au∈K，從而A(C［0，1］)?K，A的全連續性可由Arzela-Ascoli定理推出.證畢.

于是由算子T的定義，邊值問題(3)的正解等價于A在錐K中的不動點.

本文的主要工具是下面的錐拉伸與錐壓縮型的Krasnoselskii不動點定理.

引理4［7］設E為Banach空間，K是E中的一個閉凸錐，Ω1、Ω2都是K中的有界子集滿足θ∈Ω1，ˉΩ1?Ω2，T:K∩(ˉΩ2Ω1)→K為全連續映射，若下列條件之一成立:

1) ‖Tu‖≤‖u‖，?u∈K∩?Ω1，‖Tu‖≥‖u‖，?u∈K∩?Ω2；

2) ‖Tu‖≥‖u‖，?u∈K∩?Ω1，‖Tu‖≤‖u‖，?u∈K∩?Ω2.則T在K∩(ˉΩ2Ω1)中至少有一個不動點.

3 主要結果

定理 1設f:［0，1］×［0，∞)→［0，∞)連續，若下列條件之一成立:

(H1)1) ?δ＞0，使得當x∈Kδ時，f(t，x)≤12x；

2)及H＞0，使得當x≥H時，f(t，x)≥mx，

(H2)1)及 δ＞0，使得當x∈Kδ時，f(t，x)≥mx；

2) ?H＞0，使得當x≥H時，f(t，x)≤12x，則邊值問題(3)至少存在一個正解，其中Kδ=K∩ˉB(0，δ).

證明假設(H1)成立，取0＜r＜R＜+∞，令

則 θ∈Ω1且 ˉΩ1?Ω2.

首先證明，當r適當小時，有‖Au‖≤‖u‖，u∈?Ω1∩K.

取r∈(0，δ)，其中 δ為條件(H1)的 1)中的常數.從而，當u∈?Ω1∩K時，有0＜u(s)≤‖u‖ =r＜δ，?s∈(0，1)，由條件 (H1)的 1)知:對?s∈(0，1)，f(s，u(s))≤12u(s)≤12‖u‖，所以

［1］蔣達清.三階非線性微分方程正解的存在性［J］.東北師范大學學報:自然科學版，1996，28(4):6-10.

［2］姚慶六.一類奇異三階微分方程的兩點邊值問題的正解［J］.南開大學學報:自然科學版，2011，44(1):92-96.

［3］Yao Q，Feng Y.The existence of solutions for a third order two-point boundary value problem［J］.Appl Math Lett，2002，15:227-232.

［4］Jackon L K.Existence and uniqueness of solutions of boundary value problems for third order differential equations［J］.J Diff Eqns，1973，13:432-437.

［5］Cabada A.The method of lower and upper solutions for second，third，fourth and higher order boundary value problems［J］.J Math Anal Appl，1994，185:302-320.

［6］姚慶六.三階常微分方程的某些非線性特征值問題的正解［J］.數學物理學報，2003，A23(5):513-519.

［7］Li S.Positive solutions of nonlinear singular third-order two-point boundary value problem［J］.J Math Anal Appl，2006，323:413-425.

［8］姚慶六.一類非線性三階兩點邊值問題的單調迭代方法［J］.云南大學學報:自然科學版，2011，33(1):1-5.

［9］張立新.三階邊值問題的3個正解的存在性［J］.四川師范大學學報:自然科學版，2011，34(4):466-470.

［10］陳麗，胡良根，馬曉丹.奇異三階微分方程特征值問題正解的存在性［J］.應用泛函分析學報，2012，14(4):377-387.

［11］馮育強，劉三陽.一類非線性三階邊值問題的可解性［J］.工程數學學報，2007，24(3):543-546.

［12］姚慶六.一類非線性三階三點邊值問題的解和正解［J］.數學雜志，2007，27(6):704-708.

［13］孫建平，彭俊國，郭麗君.非線性三階三點邊值問題的正解［J］.蘭州理工大學學報:自然科學版，2009，35(1):139-142.

［14］趙薇.奇異三階微分方程m點邊值問題的正解［J］.四川師范大學學報:自然科學版，2013，36(2):252-257.

［15］李永祥.二階非線性常微分方程的正周期解［J］.數學學報，2002，45:481-488.

［16］郭大鈞.非線性泛函分析［M］.濟南:山東科學技術出版社，1985.