大機動飛行的魯棒自適應控制

周志久 劉 波 孫 勇

北京航天自動控制研究所，北京100854

?

大機動飛行的魯棒自適應控制

周志久 劉 波 孫 勇

北京航天自動控制研究所，北京100854

針對飛機大機動飛行時存在的模型氣動參數不確定性和外界擾動等影響因素，提出了一種基于反步法的魯棒自適應滑模控制方法。基于反步的思想，適當選取李亞譜諾夫函數回饋遞推得到不確定參數自適應律，并在最后一步結合線性滑模設計滑模控制器。對某飛機六自由度模型的大機動仿真驗證了該方法的有效性。

大機動飛行；反步自適應；滑模控制

現代高性能飛機的一個主要特點是機動性和敏捷性，其中一個重要環節是在大機動下對飛機進行控制。在大機動飛行時，氣動力和氣動力矩均成明顯的非線性特性，三軸慣性動力學嚴重耦合，不能采用常規的線性小擾動方程處理，必須采用非線性控制方法處理耦合的運動方程，才能保證飛行安全。

滑模變結構控制[1]能夠實現解耦控制，而且由于滑動模態的存在，使它對外界干擾和參數攝動具有強魯棒性，已被用于非線性飛行控制系統的設計[2]，但是系統的不確定性要滿足匹配條件[1]，而飛機在大機動時不確定性往往是不匹配的。

反步法[3]是20世紀90年代出現的自適應控制方案，是一種由前往后遞推的設計方法，以Lyapunov能量函數的收斂性為目標，設計過程中保留了系統中有用的非線性特性，既可以處理匹配不確定性又可以處理非匹配不確定性，且具有良好的過渡過程品質，然而，反步法要求系統確定性滿足可參數化表示的假設，且存在“計算膨脹”問題[3]。將滑模控制與反步控制方法相結合，既可以簡化反步控制的“計算膨脹”問題[3]，又增加了系統對非匹配不確定性的魯棒性。

文中針對非線性飛機塊嚴格反饋模型，將反步法與線性滑模相結合，設計了大機動飛行控制律。針對飛機模型中存在的氣動參數不確定性、輸入增益矩陣不確定性及未知有界干擾，基于Lyapunov穩定性理論，以一種遞歸的方式選取參數自適應律和滑模控制器。將所設計的飛控系統進行大機動仿真研究，結果證明該控制方案能控制飛機跟蹤大機動指令飛行，且具有較強魯棒性。

1 非線性飛機模型

本文的研究對象為戰斗機六自由度非線性模型，控制目的是實現姿態輸入指令φ,α,β的跟蹤，因此主要考慮由φ,α,β,p,q,r,θ構成的姿態控制系統，數學模型如下[4]：

(2)

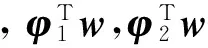
控制器設計的目的是在大機動時，在氣動參數、控制增益矩陣未知及外界干擾存在的情況下，設計控制輸入u,使得閉環系統的輸出y(t)=(φ,α,β)T漸近跟蹤期望的參考輸入yd(t)=(φd,αd,βd)T。

2 控制器設計

為滿足后續控制系統設計算法推導，在設計控制系統之前先給出如下的假設條件：

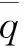
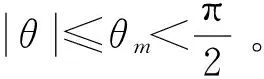
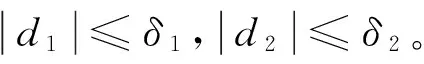
首先利用虛擬反饋定義跟蹤誤差狀態變量，對于位置跟蹤有

z1=y-yd=x1-x1d

(3)

z2=x2-x2d

(4)

其中，x2d為中間級虛擬控制變量。

對方程(3)求導得

(5)

為使每一狀態分量具有適當的漸近特性，選擇Lyapunov函數：

(6)

沿狀態軌跡對式(6)求導得，

(7)

取中間級虛擬控制變量[5]

(8)

式中，k1是對稱正定矩陣，a>0,ε>0。

將式(8)代入式(7)得

(9)

接下來與線性滑模相結合設計控制器，定義如下滑動流形

s=m1z1+z2，m1>0

(10)

對式(4)求導得

(11)

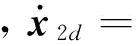
(12)

則

(13)

選擇Lyapunov函數

(14)

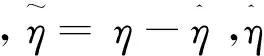
則

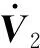
(15)

取參數自適應律為：

(16)

(17)

自適應滑模控制器：

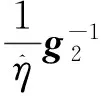
λsgn(s)+cs+m1v1s+v2s)

(18)

(19)

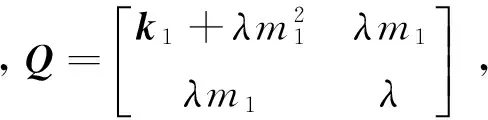
令

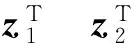
(20)

因此

(21)

對式(21)兩邊積分[6]得，

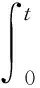
(22)

因此

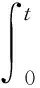
(23)

且

(24)

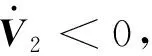
3 大機動飛行仿真

易見，即使存在較大的建模誤差和外界擾動，控制系統仍能較理想地完成大機動動作，過渡過程良好，穩態側滑小，魯棒性強。圖2是各個控制舵面偏轉的仿真曲線，可見各個舵面變化均在限幅之內，未進入飽和狀態。

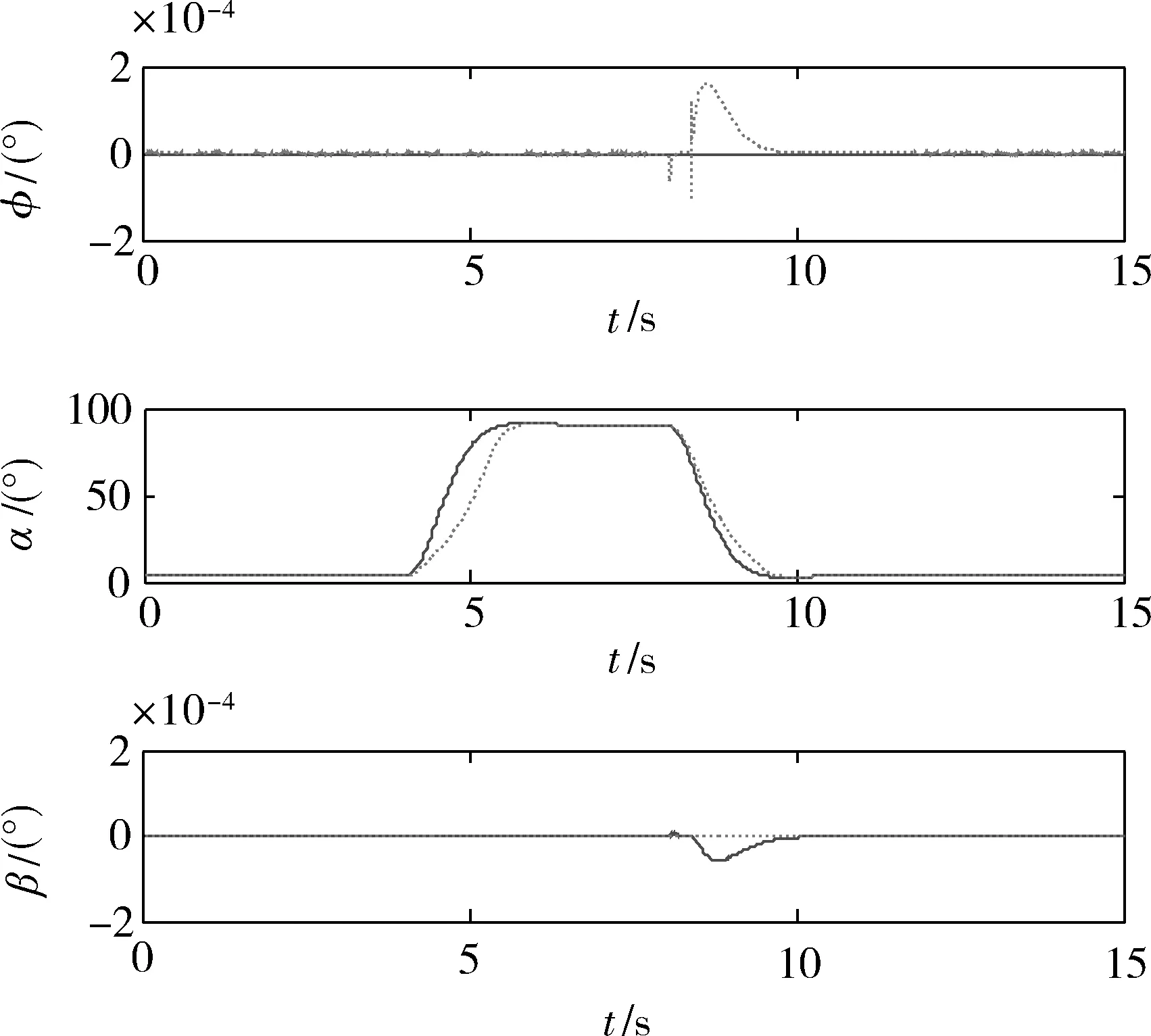
圖1 φ,α,β響應曲線

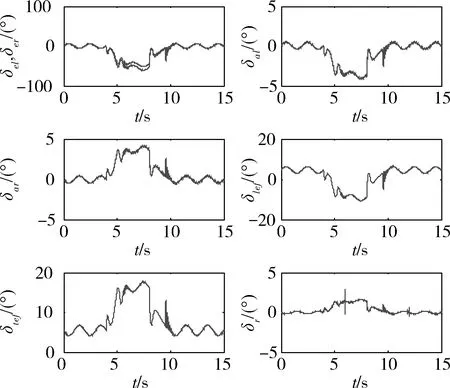
圖2 控制舵面偏轉曲線

注1：在大機動飛行時，常數空速的假設是不現實的，然而如果把空速也看作一個輸出變量，油門控制可以添加作為一個控制輸入來控制空速，文中的設計方法仍然適用。

注2: 由于滑模控制中不連續符號函數的引入，控制舵面存在抖振現象，可以在控制律式(18)中用sat函數取代符號函數消除控制抖陣。

4 結論

提出了一種基于反步法的魯棒自適應滑模控制方法以解決大機動飛行時飛機非線性動力學模型具有的參數不確定性和不確定外部干擾問題。通過數值仿真，該控制系統可以理想地跟蹤飛機大機動參考指令，具有較強的魯棒性。

[1] 高為炳.變結構控制理論基礎[M].北京：中國科學技術出版社, 1990,3.

[2] Shkolnikov I A, Shtessel Y B. Aircraft Nonminimum Phase Control in Dynamic Sliding Manifolds[J]. Journal of Guidance, Control and Dynamics, 2001，24 (3): 566-573.

[3] Krstic M, Kanellakopoulos I, Kokotovic P V. Nonlinear and Adaptive Control Design [M]. John Wiley & Sons Inc, New York, 1995.

[4] E R van Oort, L Sonneveldt, Q P Chu. A Comparison of Adaptive Nonlinear Control Designs for an Over-actuated Fighter Aircraft Model [C]. AIAA Guidance, Navigation and Control Conference and Exhibit,AIAA Inc, 2008.

[5] Ali J. Koshkouei, Alan S. I. Zinober. Adaptive Backstepping Control of Nonlinear Systems with Unmatched Uncertainty[C]. Proceedings of the 39thIEEE Conference on Decision and Control,2009: 4765-4770.

[6] 吳玉香，周東霞，胡躍明. 一類不確定非線性系統的魯棒自適應控制[J].控制理論與應用，2008,25(6):1053-1058.(Wu Y X，Zhou D X，Hu Y M.Robust Adaptive Control of a Class Uncertain Nonlinear Systems[J].Control Theory & Applications，2008,25(6):1053-1058.)

[7] Slotine J E, Li W P. Applied Nonlinear Control[M]. Engle-wood Cliffs, New Jersey: Prentice Hall, 1991.

[8] S A Snell, D F Enns. Nonlinear Inversion Flight Control for a Supermaneuverable Aircraft[J]. Journal of Guidance, Control and Dynamics, 1992,15(4):976-984.

The Robust Adaptive Control for High Maneuvers Flight

ZHOU Zhijiu LIU Bo SUN Yong

Beijing Aerospace Automatic Control Institue，Beijing 100854, China

Arobustadaptiveslidingmodecontrollerbasedonbacksteppingisproposedforhighmaneuversflightregardingmodelparametersuncertaintiesandunknowndisturbance.TheuncertainparametersadaptivelawisobtainedrecursivelyviaanappropriatechoiceofLyapunovfunctionbasedonbacksteppingprocedure,andslidingmodecontrollerisdesignedwiththelinearslidingmodeinthelaststep.Thehighmaneuversflightsimulationresultsfornon-linear6-DOFaircraftmodelshowtheeffectivenessofthecontrolmethod.

Highmaneuversflight;Backstepping;Slidingmodecontrol

2013-01-25

周志久(1982-),男，煙臺人，工程師，主要研究方向為控制系統綜合設計；劉 波(1976-),男，山東青州人，高級工程師，主要研究方向為航天器控制系統綜合設計；孫 勇(1984-),男，煙臺人，工程師，主要研究方向為飛行器控制系統綜合設計。

TP273；V249.1

A

1006-3242(2014)01-0035-05