基于貝葉斯分析框架下的VAR和DSGE模型①
陽曉明
(湘潭大學(xué)商學(xué)院,湖南湘潭411105)
1 引言
宏觀經(jīng)濟學(xué)在20世紀30年代“凱恩斯革命”中成為獨立的研究領(lǐng)域。應(yīng)用宏觀經(jīng)濟學(xué)一直是宏觀經(jīng)濟學(xué)中最為活躍的研究領(lǐng)域之一,各種新思路、新方法層出不窮。“凱恩斯革命”之后的幾十年中,由凱恩斯理論導(dǎo)出的結(jié)構(gòu)方程方法成為宏觀經(jīng)濟學(xué)實證研究的主要方向。但是20世紀70年代由于受到盧卡斯批判(Lucas critique)和宏觀經(jīng)濟模型商業(yè)應(yīng)用的沖擊,考爾斯委員會(Cowles commission)結(jié)構(gòu)性聯(lián)立方程組模型逐漸失去其在應(yīng)用宏觀經(jīng)濟學(xué)中的統(tǒng)治地位。20世紀80年代以后,由于Kydland and Prescott(1982)和Long and Plosser(1983)的開創(chuàng)性工作,第一代動態(tài)隨機一般均衡(DSGE)模型以(Kydland and Prescott為代表的RBC模型)成為宏觀經(jīng)濟學(xué)的主流理論方法,許多實證宏觀計量方法也圍繞如何估計和評價DSGE模型展開[1]。
在實證宏觀計量方法方面,經(jīng)濟學(xué)家提出了許多正式和非正式的數(shù)量方法,如向量自回歸(VAR)方法、校準(calibration)方法、一般矩估計方法(GMM)及完全信息極大似然估計(MLE)方法等等。為了減輕“經(jīng)濟理論施加的難以置信的限制”,Sims(1980)提出較少運用經(jīng)濟理論而以數(shù)據(jù)為中心的VAR方法,該方法自提出以來得到了廣泛的運用,并成為宏觀經(jīng)濟建模的基本分析工具。DSGE模型是一個數(shù)據(jù)生成過程的多元隨機表示系統(tǒng),這使我們很容易將其近似表示為VAR模型[2]。但是,簡單的DSGE模型對數(shù)據(jù)施加了很強的限制和約束條件,因而存在嚴重的模型誤設(shè)定(mis-specificaiton)問題,這使得由DSGE模型所導(dǎo)出的VAR模型常常被實際數(shù)據(jù)所拒絕(An and Schorfheide,2007)。正是由于模型誤設(shè)定和識別等問題,經(jīng)濟學(xué)家們在80年代對DSGE模型的評價一直沒有有效的正式統(tǒng)計學(xué)方法,這也是Kydland and Prescott(1982,1996)放棄正式的(概率)計量方法,轉(zhuǎn)而使用非正式的計量方法-校準方法的原因。與概率方法對計量經(jīng)濟模型的估計、檢驗和統(tǒng)計推斷不同,校準方法通過選擇宏觀經(jīng)濟數(shù)據(jù)(如國內(nèi)生產(chǎn)總值、通貨膨脹等)的一些特征化事實(如一階矩、二階矩等),設(shè)定DSGE模型的參數(shù)使模型理論矩與觀測到數(shù)據(jù)的相應(yīng)矩(特征化事實)相一致,并驗證模型能否解釋剩下的特征化事實(如各種高階矩)。但是在校準方法中,參數(shù)值和特征化事實的選取往往是任意的,沒有固定的選擇程序;而且該方法沒有參數(shù)估計結(jié)果的概率度量和統(tǒng)計檢驗。上述問題都使得校準方法缺乏穩(wěn)健性和統(tǒng)計推斷能力,而對于引入大量剛性和沖擊的大規(guī)模新凱恩斯主義DSGE模型來講,校準方法就變得更加難以執(zhí)行,而且上述缺點將變得更為嚴重。
Hansen(1982)提出的GMM方法則從一定程度上緩解了校準方法缺乏概率描述的缺點。GMM方法從某些總體距條件(正交條件)出發(fā),使樣本距與總體距盡量相一致或靠近,以此估計模型參數(shù)。但是由于工具變量的可獲得性、小樣本偏差和最優(yōu)權(quán)重矩陣的估計等問題使得GMM方法缺乏可行性和穩(wěn)健性。而且在宏觀經(jīng)濟運用中,由于該方法使用DSGE模型的歐拉方程矩條件而無需解出模型,這就使模型的識別問題顯得更為突出(Canova,2007)。Linde(2005)使用模擬數(shù)據(jù)發(fā)現(xiàn)即使沒有測量誤差,新凱恩斯主義菲利普斯曲線模型的GMM估計量在小樣本時也有嚴重的偏差,而且偏差程度隨貨幣政策行為的變化而變化,而此時完全信息極大似然估計則更具有吸引力。傳統(tǒng)的完全信息極大似然估計方法首先需要對DSGE模型的外生沖擊設(shè)定一個概率分布,然后根據(jù)模型的結(jié)構(gòu)方程推導(dǎo)出似然函數(shù),并在一定的參數(shù)空間內(nèi)極大化該似然函數(shù)。Linde(2005)發(fā)現(xiàn)無論在模型誤設(shè)定還是非正態(tài)測量誤差條件下,完全信息極大似然估計都比有限信息方法(如GMM)表現(xiàn)更好。但是由于DSGE模型非線性解的計算負擔(dān),使得大多數(shù)經(jīng)驗文獻僅僅能估計線性化的DSGE模型。而且非高斯擾動的DSGE模型、似然函數(shù)的扁平性(flatness)和多重局部極大值問題等也常常使得極大似然估計難以進行。另外極大似然估計方法對模型誤設(shè)定非常敏感,只有在模型有很好的線性近似,且模型誤設(shè)定很小時才能運行良好[3]。
同時宏觀經(jīng)濟學(xué)家們通過不斷引入一些更為實際的假定條件,使得模型的設(shè)定能進一步逼近現(xiàn)實經(jīng)濟運行,這大大改善了第一代DSGE模型的誤設(shè)定問題,也使得一些傳統(tǒng)的計量經(jīng)濟技術(shù)能用來估計、評價和預(yù)測DSGE模型。如貝葉斯VAR方法、貝葉斯DSGE方法、基于DSGE和VAR沖擊響應(yīng)函數(shù)差距的最小距離估計方法等等,其中貝葉斯VAR和貝葉斯DSGE方法得到了學(xué)術(shù)領(lǐng)域和中央銀行實際工作者的廣泛認可。
2 貝葉斯分析方法
貝葉斯分析方法是指在進行參數(shù)估計時,將參數(shù)的某些先驗信息考慮進來,將這些先驗信息與樣本信息相結(jié)合,運用貝葉斯定理得出(或更新)參數(shù)估計的統(tǒng)計學(xué)方法。假定我們要估計的參數(shù)為θ,貝葉斯估計方法將其看作隨機變量,并假定其概率密度為p(θ)。假定YT表示T個隨機樣本觀測值,則p(YT|θ)為樣本的條件概率密度,也是樣本觀測值的似然函數(shù)。p(YT,θ)為樣本觀測值和待估參數(shù)的聯(lián)合概率密度函數(shù),p(θ|YT)為給定樣本信息后參數(shù)θ的后驗概率密度,由貝葉斯定理有:
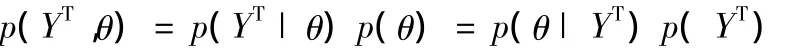
其中P(YT)≠0。由于P(YT)與θ無關(guān),可視為常數(shù),將上面表達式寫為:
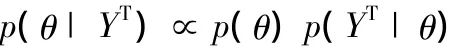
其中∝表示“成比例”,即在給定樣本信息后,待估參數(shù)的后驗概率密度與參數(shù)先驗概率密度和樣本似然函數(shù)的乘積成比例。該公式表明先驗信息通過先驗密度進入后驗密度,樣本信息通過似然函數(shù)進入后驗密度,聯(lián)合后驗密度則將所有先驗和樣本信息歸納融合其中(Zellner,1971)。在貝葉斯觀點下,待估計參數(shù)被看作隨機變量,關(guān)于參數(shù)的推斷都是以概率形式出現(xiàn)的,這使我們可以考慮盡可能大的參數(shù)空間,使模型的估計更為穩(wěn)健。許多數(shù)值模擬方法如馬爾可夫鏈蒙特卡洛方法(Markov Chain Monte Carlo)都能被用來從參數(shù)后驗分布中進行抽樣,基于這些抽樣我們可以通過數(shù)值方法來估計后驗分布的各種矩,并對參數(shù)進行統(tǒng)計推斷[4]。
經(jīng)濟學(xué)家將貝葉斯觀點運用到了許多宏觀經(jīng)濟學(xué)模型中,近年最主要的進展是貝葉斯向量自回歸(貝葉斯VAR)模型和貝葉斯動態(tài)隨機一般均衡(貝葉斯DSGE)模型。貝葉斯DSGE和貝葉斯VAR方法就是將先驗信息引入DSGE和VAR模型,運用貝葉斯觀點,使先驗信息與數(shù)據(jù)信息相結(jié)合,進而對模型的參數(shù)進行后驗推斷和預(yù)測的一種統(tǒng)計推斷方法。貝葉斯DSGE和貝葉斯VAR方法不僅有貝葉斯估計方法的一般優(yōu)點,相對于一般的DSGE和VAR模型,貝葉斯估計方法在模型的估計、評價和計算上也有較多優(yōu)勢。而且貝葉斯估計方法將經(jīng)濟理論、數(shù)據(jù)和政策分析非常好地融為一體,已成為宏觀經(jīng)濟建模和預(yù)測,歐、美國家中央銀行制定和執(zhí)行貨幣政策的基本分析框架。下面以貝葉斯VAR模型和貝葉斯DSGE模型為例,說明其基本原理和運用。
3 貝葉斯VAR和貝葉斯DSGE模型方法
3.1 貝葉斯VAR模型方法
20世紀80年代以后,經(jīng)濟學(xué)家廣泛運用VAR方法對時間序列進行分析、預(yù)測和政策分析。但是,對于由標準DSGE模型得出的限制性簡約VAR或擁有較小自由度的VAR來講,運用非限制性VAR方法進行的實證估計往往不太準確,或預(yù)測時有很大的標準差,而且難以形成良好的經(jīng)濟學(xué)理論解釋。而當數(shù)據(jù)較少,或樣本信息較弱,或待估計參數(shù)數(shù)量較多時,非限制性VAR估計將帶來過度擬和(overfitting)問題及因此導(dǎo)致的較差的預(yù)測效果(Canova,2007)。貝葉斯VAR模型則可以很好地解決非限制性VAR模型的樣本外預(yù)測表現(xiàn)、模型誤設(shè)定及數(shù)據(jù)和經(jīng)濟理論一致性等問題。
3.1.1 Minnesota先驗分布貝葉斯VAR模型
假定有T個樣本觀測值的n×1向量yt有以下p階簡約VAR模型表示:
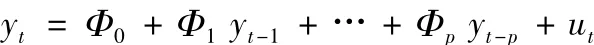
其中Φ0,Φ1,...,Φp為VAR系數(shù)參數(shù),ut為向前一步預(yù)測誤差,ut-N(0,Σu)為了改善VAR模型的樣本外預(yù)測表現(xiàn)和識別問題,Doan,Litterman and Sims(1984)和Litterman(1986)針對非限制性VAR模型的系數(shù)參數(shù)提出了Minnesota(或 Litterman)先驗分布。定義Φ =[Φ0,Φ1,…,Φ]'、α =vec(Φ)和 YT= [y1,…,yT]',Minnesota先驗分布假定α-N(0,Σα),其中α是n2(p+1)×1向量,對角陣Σα是先驗方差協(xié)方差矩陣,且是少數(shù)幾個超參數(shù)(hyperparameter)的函數(shù)。實際上Minnesota先驗分布是按逐條方程對簡約VAR模型系數(shù)參數(shù)設(shè)定先驗信息,因而在多方程結(jié)構(gòu)VAR模型占主要比重的宏觀經(jīng)濟研究中有一定局限性。針對多方程結(jié)構(gòu) VAR模型,Sims and Zha(1998)進一步發(fā)展了Litterman的思想,使用“正態(tài) -逆Wishart”先驗分布作為結(jié)構(gòu)參數(shù)的先驗信息,該先驗分布也適用于過度識別的結(jié)構(gòu)VAR模型。在實證研究方面,Robertson and Tallman(1999)根據(jù)美國主要宏觀經(jīng)濟數(shù)據(jù),使用 Minnesota、擴展的 Minnesota和 Sims and Zha(1998)等多種先驗分布,證實帶有先驗分布的貝葉斯VAR模型可以很好地提高非限制性VAR模型的預(yù)測表現(xiàn)。Cogley and Sargent(2001,2005)和 Canova et al.(2008)等則進一步放松了VAR模型的系數(shù)限制。他們允許VAR模型的系數(shù)隨時間而變化,即時間可變系數(shù)貝葉斯VAR模型(TVC-BVAR),以解釋觀察到的宏觀經(jīng)濟時間序列中結(jié)構(gòu)變化和區(qū)制轉(zhuǎn)換現(xiàn)象。Minnesota先驗BVAR模型可以在一定程度上回避VAR模型中的“維度詛咒”問題,能很好地平衡VAR模型估計中的可靠性和計算負擔(dān)問題,而且可以提供較好的短期時間序列預(yù)測[4]。當然Minnesota先驗分布的設(shè)定較多地依賴經(jīng)驗方法,缺少經(jīng)濟學(xué)解釋和理論支撐。先驗分布如太松則易造成過度擬合問題,如太緊則易造成數(shù)據(jù)信息缺失問題,而且忽視了內(nèi)生變量的聯(lián)動效應(yīng)(co-movements)信息[5]。
3.1.2 DSGE -VAR 分析方法
DSGE模型對其移動平均表示參數(shù)施加了很強的約束,盡管DSGE模型沒有有限階的VAR表示,我們?nèi)匀豢梢允褂胮階VAR模型作為DSGE模型移動平均表示的近似。DSGE模型p階VAR近似表示的滯后階數(shù)越長,則該近似表示與DSGE模型的誤差越小。非限制性VAR模型參數(shù)向量比DSGE模型參數(shù)向量的緯度大得多,因此DSGE模型對其近似VAR表示施加了很強的結(jié)構(gòu)約束。近年來,越來越多的實證研究表明DSGE模型中潛在的模型誤設(shè)定問題是不容忽視的Del Negro et al.(2007),因而由非限制性VAR模型推出的沖擊響應(yīng)函數(shù)往往與誤設(shè)定的DSGE模型推出的沖擊響應(yīng)函數(shù)有相當大的差距。為了解決DSGE模型的誤設(shè)定及數(shù)據(jù)和經(jīng)濟理論的一致性問題,Del Negro and Schorfheide(2004)提出了DSGEVAR分析方法。假定DSGE模型n×1內(nèi)生可觀測向量yt有如(4)式定義的p階簡約VAR近似表示形式,向量θ表示DSGE模型的待估計深層參數(shù),用基于參數(shù)θ的DSGE模型產(chǎn)生的T*個模擬樣本增廣實際樣本數(shù)據(jù),引入超參數(shù)λ=T*/T作為模型誤設(shè)定的度量指標。假定以參數(shù)θ為條件,VAR模型參數(shù)的先驗分布服從“正態(tài) -逆Wishart”分布形式,則運用貝葉斯定理可以得出VAR模型參 數(shù) Φ 和 Σu的 后 驗 估 計 量。DelNegroand Schorfheide(2004)認為可以使用數(shù)據(jù)驅(qū)動的方法確定超參數(shù)λ的取值,即最大化超參數(shù)λ的邊際似然函數(shù)
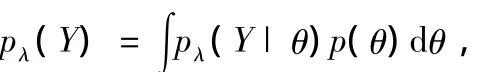
其中pλ(Y|θ)= ∫p(Y|Φ,Σu)p(Φ,Σu|θ)d(Φ,Σu)。
且是超參數(shù)λ的函數(shù)。函數(shù)pλ(Y)衡量了可以在多大程度上放松DSGE模型的限制,以平衡樣本內(nèi)擬合和DSGE模型的復(fù)雜性,也可以看作DSGE模型誤設(shè)定程度的時間序列證據(jù)(Del Negro et al.2007)。為了求得最優(yōu)的由超參數(shù)λ表示的模型設(shè)定形式,設(shè)定超參數(shù)λ的格點區(qū)間為∧ =(l1,l2,……,lq),l1=n(p+2)/T,lq= ∞。
對該格點區(qū)間極大化λ的邊際似然函數(shù),則λ的最優(yōu)估計量^λ由下式定義:
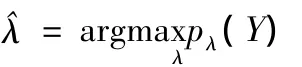
DSGE-VAR方法實際上是將DSGE模型作為VAR模型的先驗信息,一方面放松DSGE模型的參數(shù)限制,以提高DSGE模型的擬合程度,并修正DSGE模型的誤設(shè)定;另一方面限制VAR模型的參數(shù)自由度,以提高VAR模型的預(yù)測表現(xiàn),并提高VAR模型識別和擬合的精確度,取得理論和數(shù)據(jù)的一致性和平衡。DSGE-VAR估計方法使我們能夠考慮介于DSGE模型和非限制VAR模型之間的模型設(shè)定形式,可以在由超參數(shù)λ代表的一個連續(xù)統(tǒng)的中間模型空間中選擇最好的模型設(shè)定形式[6]。通過極大化λ的邊際似然函數(shù)選擇超參數(shù)λ,此時深層參數(shù)θ的后驗分布可以被解釋為用作相應(yīng)VAR先驗分布的最好DSGE模型設(shè)定形式的后驗估計,而超參數(shù)λ的后驗分布則給出了DSGE模型可靠性及所代表的經(jīng)濟約束經(jīng)驗相關(guān)性的度量指標。Adjemian and Paries(2008)改進了DSGE-VAR分析,他們認為 Del Negro and Schorfheide(2004)和Del Negro et al.(2007)使用少數(shù)幾個值以格點化超參數(shù)λ,在此基礎(chǔ)上通過極大化邊際似然函數(shù)以求得最優(yōu)超參數(shù)值的方法至少在計算上是無效率的,而且是非貝葉斯觀點的。與Del Negro and Schorfheide(2004)依照超參數(shù)λ的格點取值作循環(huán)估計不同,他們將超參數(shù)λ看作另一個深層參數(shù),并對其賦予一定的先驗分布信息p(Y),再與其他參數(shù)的先驗分布信息相結(jié)合對模型進行估計和推斷。
3.2 貝葉斯DSGE模型方法
在DSGE-VAR方法中,參數(shù)由最小化非限制性VAR系數(shù)和由DSGE模型導(dǎo)出的近似VAR系數(shù)(帶有跨方程約束)的差距所決定。與DSGE-VAR方法相比,貝葉斯DSGE估計方法則要求直接擬合所有觀測到的時間序列數(shù)據(jù),在一定程度上是校準方法和極大似然估計方法的折衷,是動態(tài)經(jīng)濟理論、計量經(jīng)濟方法和計算機技術(shù)的有機融合。Geweke(1999)認為DSGE模型有兩種不同的計量經(jīng)濟解釋:弱計量解釋和強計量解釋。弱計量經(jīng)濟解釋主要是指Kydland and Prescott(1982,1996)的校準方法,該方法僅僅提供了數(shù)據(jù)生成過程的部分描述。而強計量經(jīng)濟解釋則提供了數(shù)據(jù)生成過程的整體描述,因而也更為可信和穩(wěn)健,主要指的是傳統(tǒng)極大似然估計方法和貝葉斯估計方法。
假定用 YT=[y1,...,yT]'表示DSGE模型中n ×1階可觀測向量yt的T個觀測值,其聯(lián)合條件概率密度函數(shù)(模型的后驗核)為
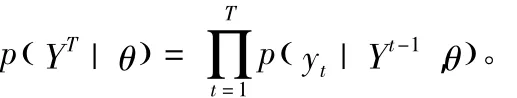
我們可以由DSGE模型的線性狀態(tài)空間表示形式,使用卡爾曼濾波(Kalman filter)算法推導(dǎo)聯(lián)合概率密度函數(shù)、卡爾曼濾波更新公式和預(yù)測公式。假定DSGE模型深層參數(shù)向量θ的先驗概率密度為p(θ),由貝葉斯定理及L(θ|YT)=p(YT|θ)
可得參數(shù)θ的后驗密度函數(shù)為
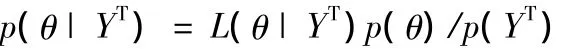
其中L(θ|YT)是基于觀測數(shù)據(jù)的似然函數(shù)。首先運用數(shù)值方法最大化對數(shù)似然函數(shù)及對數(shù)參數(shù)先驗密度的和(邊際數(shù)據(jù)密度函數(shù)是常數(shù)),以獲得參數(shù)的后驗眾數(shù)θmode:

相對傳統(tǒng)極大似然估計方法,㏑p(θ)可以被看作對似然函數(shù)的懲罰函數(shù)(penalty function)。再將后驗眾數(shù)θmode作為初始值(或其他給定初始值),由MCMC抽樣方法(如隨機游走Metropolis-Hastings算法),從后驗分布中獲取抽樣,由數(shù)值積分方法計算所需參數(shù)的各階后驗距和置信區(qū)間,并檢驗其收斂性[7]。最后根據(jù)計算的各階距、置信區(qū)間和沖擊響應(yīng)函數(shù),由設(shè)定的損失函數(shù)(loss function)對模型進行推斷和評價。以貝葉斯VAR模型類似,貝葉斯DSGE模型使用參數(shù)的一個先驗分布作為似然函數(shù)的懲罰函數(shù),將數(shù)據(jù)信息和先驗信息相結(jié)合,對模型作出估計和推斷。與DSGE模型的傳統(tǒng)極大似然估計相比,貝葉斯DSGE模型對參數(shù)賦予了更為合理的空間,有效地避免了傳統(tǒng)極大似然估計中似然函數(shù)在某些參數(shù)空間的扁平性問題和多重局部極大值問題。而且當模型的誤設(shè)定程度很高時,極大似然估計方法常常得出荒謬的估計結(jié)果,而貝葉斯DSGE估計方法可以有效地應(yīng)對這類“錯誤的”模型,它可以運用信息性先驗(informative prior)分布,充分考慮到模型的不確定性和模型誤設(shè)定問題,得出相對合理的估計結(jié)果。Smets and Wouters(2003,2007)發(fā)展了一個粘性價格和工資的新凱恩斯主義DSGE模型,他們用貝葉斯估計方法分別估計了歐元區(qū)和美國的主要宏觀經(jīng)濟數(shù)據(jù),他們發(fā)現(xiàn)新凱恩斯主義DSGE模型能很好地擬合歐元區(qū)和美國的時間序列數(shù)據(jù)。在樣本外預(yù)測方面,貝葉斯DSGE模型比VAR模型或貝葉斯VAR模型表現(xiàn)更好(有更大的似然函數(shù)值)。值得注意的是貝葉斯實證文獻中的很多作者都來自美國和歐元區(qū)的中央銀行,他們估計的貝葉斯DSGE模型正在成為中央銀行進行宏觀經(jīng)濟分析和預(yù)測,并依此制定和執(zhí)行貨幣政策的基本分析框架。如Smets and Wouters(2003,2007)估計的新凱恩斯主義DSGE模型,該框架已成為歐州中央銀行分析宏觀經(jīng)濟波動和經(jīng)濟周期,制定、執(zhí)行和評價貨幣政策的重要分析工具[8]。
由此看來,當代應(yīng)用宏觀經(jīng)濟方法經(jīng)歷了一個由比較強調(diào)經(jīng)濟理論和政策分析,如RBC模型的校準方法;到比較強調(diào)樣本數(shù)據(jù)生成機制和模型擬合程度,如VAR模型;進一步到比較強調(diào)預(yù)測表現(xiàn)、模型比較和政策分析,如貝葉斯VAR模型和DSGE-VAR方法;再到經(jīng)濟理論和數(shù)據(jù)相結(jié)合,模型擬合、預(yù)測與政策分析并重(如貝葉斯DSGE模型和DSGE-VAR方法)的發(fā)展道路。所使用的宏觀經(jīng)濟模型也由確定性模型轉(zhuǎn)變?yōu)槌浞煮w現(xiàn)經(jīng)濟中不確定性的隨機模型,由假定模型就是正確的數(shù)據(jù)生成過程到充分考慮到模型誤設(shè)定和靈活性等問題的更為貼近現(xiàn)實的經(jīng)濟模型。在這個過程中,各種理論和方法相互借鑒,也體現(xiàn)了應(yīng)用宏觀經(jīng)濟方法進一步“融合”的趨勢。正如Blanchard(2008)指出的,在過去的20年中宏觀經(jīng)濟學(xué)無論在圖景和方法論上都有廣泛的“收斂”跡象[9]。
4 貝葉斯估計方法在我國宏觀經(jīng)濟建模中的適用性
4.1 宏觀經(jīng)濟運行機制和模型設(shè)定
我國經(jīng)濟運行正處于由計劃經(jīng)濟向市場經(jīng)濟的轉(zhuǎn)軌時期,社會經(jīng)濟結(jié)構(gòu)和國家宏觀經(jīng)濟政策的制定和執(zhí)行也處于不斷演化過程中。這種經(jīng)濟的“過渡性”導(dǎo)致了利益分配機制及資源約束條件等的不斷變化,也因此導(dǎo)致經(jīng)濟主體的行為很不穩(wěn)定,宏觀經(jīng)濟運行常常大起大落并處于不同的體制區(qū)(regime)中。經(jīng)濟主體行為的不穩(wěn)定使得宏觀經(jīng)濟運行的結(jié)構(gòu)參數(shù)也很不穩(wěn)定,常常出現(xiàn)跳躍,并處于不斷變化過程中。因此我國宏觀經(jīng)濟運行中常常會出現(xiàn)結(jié)構(gòu)斷點,宏觀經(jīng)濟的數(shù)據(jù)生成過程和參數(shù)出現(xiàn)結(jié)構(gòu)變化。一般經(jīng)典計量方法都假定經(jīng)濟運行服從一個數(shù)據(jù)生成過程,結(jié)構(gòu)參數(shù)被假定為固定不變的常數(shù),從而使用普通最小二乘(OLS)或傳統(tǒng)極大似然方法(MLE)對參數(shù)進行估計和統(tǒng)計推斷。而我國的宏觀經(jīng)濟數(shù)據(jù)可能不同時期服從不同的數(shù)據(jù)生成過程和參數(shù)結(jié)構(gòu),因此使用經(jīng)典計量方法(一般僅假定一個數(shù)據(jù)生成過程)對我國的宏觀經(jīng)濟數(shù)據(jù)進行的計量分析和統(tǒng)計推斷往往是不妥當?shù)模纱说贸龅暮暧^經(jīng)濟政策建議往往也是不正確的。而貝葉斯估計方法將模型參數(shù)看作是隨機變量,并對待估計的模型參數(shù)賦予一個先驗概率分布,根據(jù)貝葉斯定理得出(更新)對模型參數(shù)的概率推斷。可以看出,貝葉斯估計方法特別適用于像我國這樣的轉(zhuǎn)軌經(jīng)濟國家的經(jīng)濟數(shù)據(jù)建模和政策分析,該方法可以充分考慮經(jīng)濟處于不同體制區(qū)的“過渡性”,并能允許經(jīng)濟參數(shù)的結(jié)構(gòu)變化。
4.2 宏觀經(jīng)濟數(shù)據(jù)的可獲得性和質(zhì)量
相對于經(jīng)典估計方法,貝葉斯估計方法對于小樣本的估計是更為穩(wěn)健的(Zeller,1971)。在大樣本下貝葉斯估計方法等價于經(jīng)典估計方法,使用不同先驗信息的貝葉斯估計結(jié)果的差別在大樣本下也將消失。在實證研究中,宏觀經(jīng)濟時間序列的數(shù)據(jù)一般較短(小樣本),即使在美國這樣宏觀經(jīng)濟數(shù)據(jù)較為豐富的國家也是如此,我國的宏觀經(jīng)濟時間序列數(shù)據(jù)在這方面的矛盾就更為突出(如我國1992年以后才有較完整的主要宏觀經(jīng)濟變量的季度數(shù)據(jù))。較短的宏觀經(jīng)濟數(shù)據(jù)使得以往運用經(jīng)典計量方法(如OLS或MLE)估計的中國宏觀經(jīng)濟模型往往是不穩(wěn)健的,而貝葉斯方法能很好地解決我國宏觀經(jīng)濟時間序列較短的問題。另外,貝葉斯估計方法使我們可以結(jié)合許多國內(nèi)微觀計量研究的成果及其他宏觀研究文獻(可作為先驗信息),對模型進行估計、推斷和評價,并獲得更為穩(wěn)健的計量估計結(jié)果。而且,我國的宏觀經(jīng)濟數(shù)據(jù)存在統(tǒng)計口徑不一致和相當程度的測量誤差,貝葉斯估計方法則可將這些誤差看作隨機擾動,并賦予一定的先驗信息結(jié)構(gòu),從而在一定程度上克服我國宏觀經(jīng)濟數(shù)據(jù)的口徑不一致和測量誤差問題。綜上所述,貝葉斯估計方法非常適合我國轉(zhuǎn)軌經(jīng)濟的特征,可以很好地解決我國宏觀經(jīng)濟數(shù)據(jù)的可獲得性和質(zhì)量等問題。該方法將成為我國宏觀經(jīng)濟建模和估計,中央銀行制定和執(zhí)行貨幣政策的有力工具。
5 結(jié)論
本文回顧了應(yīng)用宏觀經(jīng)濟學(xué)的主要方法和新進展后認為:現(xiàn)有校準、向量自回歸、一般矩方法和極大似然估計等方法都存在諸多缺點,而貝葉斯分析框架的引入能有效地應(yīng)對這些問題。貝葉斯分析框架是宏觀經(jīng)濟學(xué)從更為現(xiàn)實的微觀基礎(chǔ)出發(fā),充分考慮到模型不確定性和結(jié)構(gòu)變化,以更為切實可行的政策分析為目標取得的重大方法論進展。該方法能很好地將理論與數(shù)據(jù)、微觀文獻和宏觀研究相結(jié)合,能很好地解決DSGE模型估計中的識別和誤設(shè)定問題,而且很適合進行模型的比較和宏觀經(jīng)濟政策分析。由于我國宏觀經(jīng)濟體制和結(jié)構(gòu)的特殊性及宏觀經(jīng)濟數(shù)據(jù)的特點,貝葉斯方法將在我國宏觀經(jīng)濟建模和預(yù)測,中央銀行制定和執(zhí)行貨幣政策過程中發(fā)揮重要作用。
[1]Adjemian S.,M.Darracq Paries.Assessing the international spillovers between the US and the euro area:evidence from a two-country DSGE-VAR[Z].Working Paper,European Central Bank,January 2008.
[2]An,Sungbae,and Frank Schorfheide.Bayesian Analysis of DSGE Models[J].Econometric Reviews,2007,26(24):113–72.
[3]Blanchard Olivier J.The State of Macro[Z].NBER Working Paper,14259,2008.
[4]Canova,F(xiàn)abio.Methods for Applied Macroeconomic Research[M].NJ:Princeton University Press,2007.
[5]Canova,F(xiàn)abio,Luca Gambetti,and Evi Pappa.The Structural Dynamics of US Output and Inflation:What Explains the Changes[J].Journal of Money,Credit,and Banking,2008.
[6]Cogley,Timothy,and Thomas J.Sargent.Evolving Post- World War II U.S.Inflation Dynamics[C]//NBER Macroeconomic Annual,2001.
[7]Cogley,Timothy,and Thomas J.Sargent.Drifts and Volatilities:Monetary Policy and Outcomes in the Post WWII U.S.[J].Review of Economic Dynamics,2005(8):262-302.
[8]DeJong,David N.,Beth F.Ingram,and Charles H.Whiteman.A Bayesian Approach to Dynamic Macroeconomics[J].Journal of Econometrics,2000(98):203-223.
[9]Del Negro,Marco and Frank Schorfheide.Priors From General Equilibrium Models for VARs[J].International Economic Review,2004(45):643-673.

