Poisson方程三類問題的通解
郭時光
(1.四川理工學院理學院, 四川自貢643000;2.人工智能四川省重點實驗室, 四川自貢643000)
Poisson方程三類問題的通解
郭時光1,2
(1.四川理工學院理學院, 四川自貢643000;2.人工智能四川省重點實驗室, 四川自貢643000)
研究二維到四維空間上Poisson方程。采用求出其通解的方法,分別給出了該方程Cauchy問題、Direchlet問題和Neunmann問題的通解的解析表達式,從而得出其后面兩類問題均存在無限多個解的結論。
Poisson方程;Direchlet問題;Neunmann問題;推遲勢;正規解;降維法
對于半空間上Poisson方程Direchlet問題[1-2],如果應用Poisson公式[3-4]求解,一方面,很難判斷所得解[5-11]是否正規,另一方面,當定解區域是半空間時,就缺乏合理性,并且導致所得解不全等謬誤。作為改善,需要重新分析這個問題。
1 二維Poisson方程Cauchy問題
1.1二維Poisson方程的通解
考察二維空間Poisson方程:
uxx+uyy=f(x,y)(-∞ (1) 做變換ξ=x-jy,η=x+jy,得 uξη=F(ξ,η) (2) 其中,F(ξ,η)=f(x,y)。將η視為常數,方程(2)關于ξ從ξ到η積分,得 (3) 將ξ視為常數,方程(3)關于η從ξ到η積分,得 其中,g1是可積函數,h1是可微函數,而 將原自變數代回上式,得解 (4) 式(4)即是二維Poisson方程(1)的通解公式。 1.2二維推遲勢公式 設一維齊次Cauchy條件 u|y=0=0,uy|y=0=0(-∞ (5) 考察由方程(1)與條件(5)組成的Cauchy問題。將通解式(4)用條件(5)計算,分別得 g(x)+h(x)=0 g′(x)-h′(x)=0?g(x)-h(x)=c (6) 其中,積分路徑為直線段。解的這個表達式稱為二維推遲勢公式。 定理1對于由方程(1)與條件(5)組成的Cauchy問題,如果函數f具有連續的各個偏導數,則函數(6)是該問題的正規解。 證將式(6)的函數u=u(x,y)分別代入該問題中的各個項計算,得 f1[x-j(y-τ),τ]}dτ+f(x,y)- dτ=f(x,y) 由此可知,式(6)中的函數u=u(x,y)是所述問題的正規解。證畢。 二維Laplace方程非齊次條件Cauchy問題的一般形式為: (7) 為了求解,采用將Cauchy條件齊次化法。在問題(7)中,令 u=v+μ(x)+yψ(x) (8) 則 (9) 用二維推遲勢公式可求得問題(9)的解。將這個解代入式(8),化簡得 (10) 驗證即知,有: 定理2在問題(7)中,如果函數μ(x)與ψ(x)均具有二階導數,則表達式為式(10)的解是該問題的正規解。 1.3非齊次Cauchy問題 設非齊次條件Cauchy問題 (11) 用疊加原理,由定理1與定理2,可得: 定理3如果函數f具有連續的各個偏導數,函數μ與ψ均具有連續的各個二階偏導數,則該問題存在正規解,其表達式為: w=w(x,y)= (12) 例1求二維Laplace方程vxx+vyy=0在全平面上的所有解。 解用式(4),得方程vxx+vyy=0的復數通解 v=g(x+jy)+h(x-jy) (13) 由此可見,該方程的實通解可以表示為: (14) 其中,g,h均為可連續微分二次的任意函數。 例2求解上半平面Poisson方程Direchlet問題 uxx+uyy=f(x,y);u|y=0=μ(x) (15) 解 用公式(12),得問題的一個解為: (16) 設v的是問題(15)對應齊次定解問題的解,即 vxx+vyy=0;v|y =0=0 用泛定方程的通解式(14)代入,得 (17) 其中,h為可連續微分二次的任意函數。根據疊加原理,得問題(15)的通解為: u=u0(x,y)+v(x,y) 其中,u0(x,y),v(x,y)分別為式(16)與(17)所示。 例3求解上半平面Poisson方程Neumann問題 uxx+uyy=f(x,y);uy|y=0=ψ(x) (18) 解用公式(12),得問題的一個解為: (19) 設v是問題(18)所對應全齊次定解問題的解,即 vxx+vyy=0;vy|y=0=0 用式(14)代入,得 (20) 其中,g為可連續微分二次的任意函數。根據疊加原理,得問題(18)的通解為: u=u0(x,y)+v(x,y) 其中,u0(x,y),v(x,y)分別為式(19)與(20)所示。 2.1四維推遲勢公式 設四維無限區域Poisson方程 uxx+uyy+uzz+uww=f(x,y,z,w) (21) (22) 易知,如果u=u(x,y,z,w)連續,則有 (23) 球半徑還可以擴展到負數,且有 (24) 將球面平均值中的積分用球面坐標表示,得 (25) 其中, xr=x+rcosθsinφ yr=y+rsinθsinφ zr=z+rcosφ 設函數u=u(x,y,z,w)是方程(21)的解。用函數u(xr,yr,zr,w)關于θ的周期性,得 u(xr,yr,zr,w)dθdφ= u(xr,yr,zr,w)sinφdθ}dφ= 將上式兩邊同乘以r,得 (26) 引入三維齊次Cauchy條件 u|w=0=0,uw|w=0=0(-∞ (27) 則其球面平均值滿足 [ru(x,y,z,w;r)]|w =0=0 [ru(x,y,z,w;r)]w|w =0=0 (28) 考察由方程(25)與條件(27)組成的Cauchy問題。用二維推遲勢公式,得其解 (29) 令r→0,式(28)左邊用式(22),右邊用L/Hospital法則,交換極限與積分次序,得 將f的球面平均值積分表達式代入,并使用球面坐標,化為重積分,即可得 (x+jτcosθsinφ,y+jτsinθsinφ,z+jτcosφ,w-τ)dθ (30) 式(29)就是方程(21)與條件(26)所組成Cauchy問題解的表達式,稱為四維推遲勢公式。驗證即知,有: 定理4方程(21)與條件(26)組成的Cauchy問題中,如果函數f具有連續的各個二階偏導數,則函數(29)是該問題的正規解。 2.2四維Kirchhoff公式 設有四維空間Laplace方程的Cauchy問題 (31) 采用將Cauchy條件齊次化法,然后利用四維推遲勢公式計算,得其解 u=u(x,y,z,w)= jwsinθsinφ,z+jwcosφ)]+ wψ(x+jwcosθsinφ,y+jwsinθsinφ,z+ jwcosφ)}dθ (32) 驗證即知,有: 定理5在問題(30)中,如果函數μ與ψ均具有連續的各個三階偏導數,則函數(31)是該問題的正規解。 2.3四維Cauchy問題 設四維Cauchy條件 u|w=0=μ(x,y,z),uw|w=0=ψ(x,y,z) (33) 根據定理4和定理5,用疊加原理,得 定理6方程(21)與條件(32)組成的Cauchy問題中,如果函數f具有連續的各個二偏導數,函數μ與ψ均具有連續的各個三階偏導數,則該問題存在正規解,其表達式為式(29)與式(32)的兩個函數之和。 3.1三維推遲勢公式 考察三維空間Poisson方程 uxx+uyy+uzz=f(x,y,z)(-∞ (34) 設三維齊次Cauchy條件為: u|z=0=0,uz|z=0=0(-∞ (35) 用Hadamard降維法。去掉四維推遲勢公式中關于變量z的因素,然后換w→z,并將積分作代換sinφ=ρ,這樣就能得到方程(33)與條件(34)組成的Cauchy問題解的表達式 (x+jτρcosθ,y+jτρsinθ,z-τ)dθ (36) 表達式(35)稱為三維推遲勢公式。驗證即知,有: 定理7方程(33)與條件(34)組成的Cauchy問題中,如果函數f具有連續的各個二階偏導數,則函數(35)是該問題的正規解。 3.2三維Poisson公式 設三維空間Laplace方程Cauchy問題 (37) 采用將Cauchy條件齊次化方法,用推遲式公式,得其解 zψ(x+jzρcosθ,y+jzρsinθ)}dθ (38) 驗證即知,有: 定理8在問題(36)中,如果函數μ與ψ均具有連續的各個三階偏導數,則表達式為式(37)的解是該問題的正規解。 3.3三維Cauchy問題 設三維非齊次Cauchy條件 u|z=0=μ(x,y),uz|z=0=ψ(x,y) (39) 根據定理7和定理8,用疊加原理,可得: 定理9方程(33)與條件(38)組成的Cauchy問題中,如果函數f具有連續的各個二偏導數,函數μ與ψ均具有連續的各個三階偏導數,則該問題存在正規解,其表達式為式(35)與式(37)的兩個函數之和。 由方程(33)與條件(38)組成的Cauchy問題中,如果去掉條件項uz|z=0=ψ(x,y),則問題變為Direchlet問題,其通解仍然如定理3所述,但是其中ψ則為任意函數;如果去掉條件項u|z=0=μ(x,y),則問題變為Neumann問題,其通解仍然如定理3所述,但是其中μ則為任意函數。 如果函數f具有連續的各個二偏導數,函數μ與ψ均具有連續的各個三階偏導數,則驗證可知,這樣所得的解是正規解。 由此可見,Poisson方程Direchlet問題和Neumann問題若存在解,則其解均為無窮多。 [1] 李明奇,覃思義.平面中Poisson方程的Dirichlet問題[J].大學數學,2009,25(4):146-150. [2] 黃永水.隨機Poisson方程Dirichlet大地邊值問題的隨機積分解[J].武漢大學學報:信息科學版,2005,30(10):33-38. [3] 柳志千,黃端山.Poisson方程Dirichlet問題的解在角點附近的性質[J].韶關學院學報:自然科學版,2005(3):23-27. [4] 復旦大學數學教研室.數學物理方程[M].上海:復旦大學出版社,2001. [5] 錢偉長.格林函數和變分法在電磁場和電磁波計算中的應用[M].上海:上海大學出版社,2000. [6] 王元明.數學物理方程與特殊函數[M].4版.北京:高等教育出版社,2012. [7] 沈婷婷,馬和平.二維Poisson方程的Legendre Tau方法的誤差估計[J].上海大學學報:自然科學版,2011,17(3):33-38. [8] Li Guozhen.The existence theorems of the random solutions for random Hammerstein equation with random kernel[J].applied mathematics letters,2002,15(1):103-105. [9] Zhu Chuanxi,Chen Chunfang Calculations of random fixed point index[J].Jaurmal of mathematical analysis and applications,2008,339(2):839-844. [10] 周 敏,高 挺,陳艷霞.基于BP神經網絡的液壓缸市場價格估算模型[J].中國科技論文在線,2014,7(10):1010-1014. [11] 馮雪飛,丁日佳.基于人工神經網絡的單因素特種設備事故預測[J].中國科技論文在線,2014,7(10):1002-1009. General Solution of Three Problems for Poisson Equation GUOShiguang1,2 (1.School of Science, Sichuan University of Science & Engineering, Zigong 643000, China; 2. Artificial Intelligence of Key Laboratory of Sichuan Province, Zigong 643000, China) Researching the Poisson equations on 2 d to 4 d spaces. Through the method of finding out their general solutions, the analytic expressions of the general solutions of Cauchy problem, Direchlet problem and Neunmann problem for the equation are given respectively. Thus the conclusion that there are an unlimited number of solutions for the two behind types of problems is obtained. Poisson equation;Direchlet problem; Neunmann problem; Retarded potential; Formal solution; Dimension reduction method 2014-05-27 人工智能四川省重點實驗室開放基金項目(2012RYY04) 郭時光(1955-),男,重慶榮昌人,副教授,主要從事數學物理方程方面的研究,(E-mail)youare20002000@qq.com 1673-1549(2014)06-0075-05 10.11863/j.suse.2014.06.19 O175.13 A





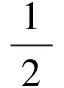
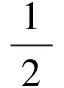
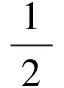
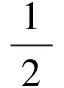


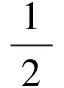
2 四維Poisson方程Cauchy問題










3 三維Poisson方程Cauchy問題


4 結束語

