大型液壓挖掘機的動力系統(tǒng)靜彎矩超限問題分析

李佳林，李 光

（太原重工技術(shù)中心，山西 太原 030024）

引言

康明斯發(fā)動機[1]在安裝時對后端面的靜彎矩有上限要求，用戶在使用時必須予以考慮。對于中小功率發(fā)動機來說，通常的安裝布置即能滿足靜彎矩要求。但對于大功率發(fā)動機，采用通常的安裝布置往往不能滿足靜彎矩要求。以某大型液壓挖掘機[2]的動力系統(tǒng)的安裝布置為例，對多種安裝布置方案進行了深入的分析和對比。動力系統(tǒng)包含QSK50發(fā)動機、分動箱和泵總成，其中發(fā)動機包含發(fā)動機主體和飛輪殼，發(fā)動機主體與飛輪殼的連結(jié)面處要求的最大靜彎矩為6 100 N?m，發(fā)動機通過飛輪殼的法蘭口與分動箱固定連接，其安裝布置示意簡圖見圖1，其中發(fā)動機質(zhì)量為6 717 kg，分動箱質(zhì)量為3 200 kg，泵總成質(zhì)量為

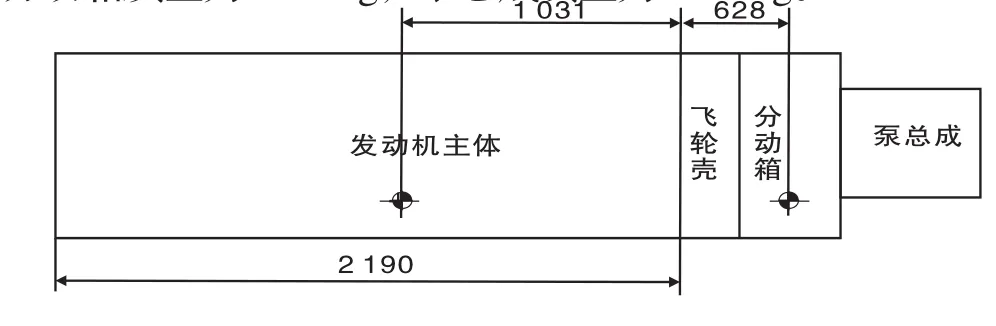
圖1 某大型液壓挖掘機的動力系統(tǒng)示意圖（mm）

1 通常的安裝布置方案分析

通常的安裝布置方案為發(fā)動機前端左右做安裝點，發(fā)動機后端飛輪殼處不做安裝點，分動箱地腳做安裝點，俗稱“兩點支撐”，圖2為該方案的安裝布置示意圖。

圖2 方案1的安裝布置示意圖

由于分動箱殼體為鑄鐵，所以可以忽略分動箱輸出側(cè)泵總成對輸入側(cè)的彎矩影響。根據(jù)材料力學中靜定結(jié)構(gòu)原理，建立力學模型（見圖3）。

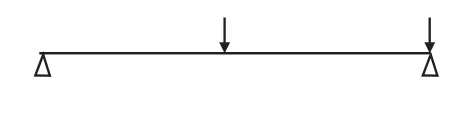
圖3 方案1的力學模型簡圖

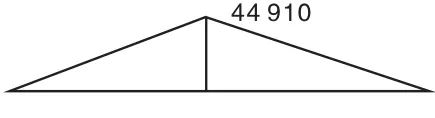
圖4 方案1的彎矩圖（N·m）

設(shè)左側(cè)支點處支反力為RA，以右側(cè)支點為力矩中心列出力矩平衡方程式：

繪制的彎矩圖如圖4所示。

由圖4可知連結(jié)面的靜彎矩M為：

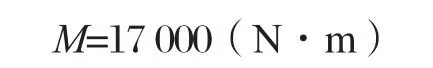
2 在飛輪殼兩側(cè)加安裝點的方案分析（方案2）

此方案是在“兩點支撐”的基礎(chǔ)上，在飛輪殼兩側(cè)各加一個輔助安裝點，以期降低連結(jié)面的靜彎矩，俗稱“三點支撐”，圖5為該方案的布置示意圖[1]。

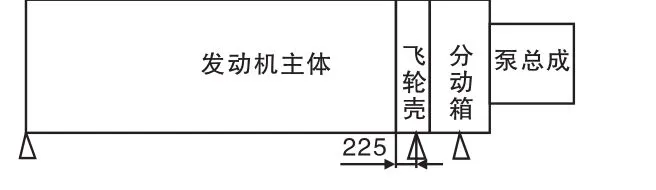
圖5 方案2的安裝布置示意圖（mm）

同理，由于分動箱殼體為鑄鐵，所以可以忽略分動箱輸出側(cè)泵總成對輸入側(cè)的彎矩影響。根據(jù)材料力學中靜不定結(jié)構(gòu)原理，建立力學模型（見圖6）。

圖6 方案2的力學模型簡圖

圖7 方案2的彎矩圖（N·m）

將中間支點改為自由鉸鏈，并加等價約束（彎矩M1和支反力R1），則連續(xù)梁變?yōu)?個簡支梁，根據(jù)三彎矩方程可求得：

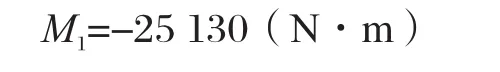
設(shè)左側(cè)支點處支反力為RA，再以中間支點為力矩中心對左側(cè)簡支梁列出力矩平衡方程式:

繪制彎矩圖如圖7所示。

由圖7可知連結(jié)面的靜彎矩為：

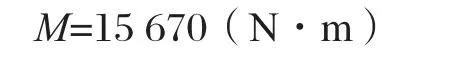
3 安裝點可平移調(diào)整的方案分析（方案3）

該方案是將飛輪殼與分動箱用橫梁固定連接后，在橫梁上做安裝點，安裝點可根據(jù)需要布置在橫梁的合適位置，從而實現(xiàn)了安裝點可沿軸向做適量平移調(diào)整的效果，圖8為此方案的布置示意圖。

同理，由于分動箱殼體為鑄鐵，所以可以忽略分動箱輸出側(cè)泵總成對輸入側(cè)的彎矩影響。根據(jù)材料力學中靜定結(jié)構(gòu)原理，建立力學模型如圖9所示[2]。

圖8 方案3的安裝布置示意（mm）

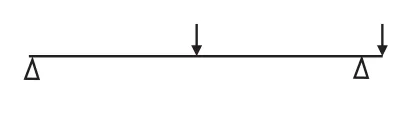
圖9 方案3的力學模型簡圖

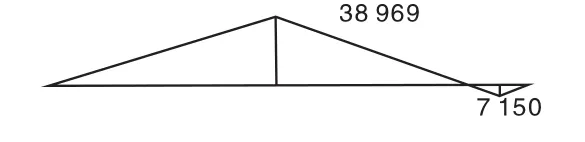
圖10 方案3的彎矩圖（N·m）

設(shè)左側(cè)支點處支反力為RA，以右側(cè)支點為力矩中心列出力矩平衡方程式：

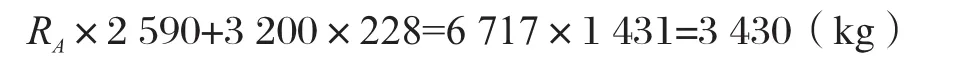
發(fā)動機重心處的彎矩MG1為

右側(cè)支點處的彎矩MB為

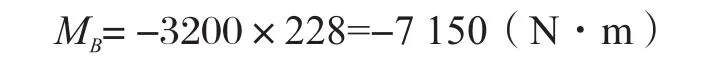
繪制彎矩圖如圖10所示。

由圖10可知連結(jié)面的靜彎矩為：

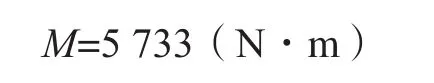
4 結(jié)語

根據(jù)以上計算可知，方案1中聯(lián)結(jié)面的靜彎矩約為允許值的2.79倍；方案2中聯(lián)結(jié)面的靜彎矩約為允許值的2.57倍；方案3中聯(lián)結(jié)面的靜彎矩小于允許值。據(jù)此，可以得出新安裝布置方案方案3是有效可行的。

[1] 王文山.柴油發(fā)動機管理系統(tǒng)[M].北京:機械工業(yè)出版社,2010.

[2] 同濟大學方,等.單斗液壓挖掘機[M].北京:中國建筑工業(yè)出版社,1980.