關于對大型圓弧板件的技術攻關

山西省長治市清華機械廠 (046012) 胡秀文

1.板件的結構特點

如圖1所示，該件為方330 mm×330 mm的弧形板件，表面粗糙度值Ra=3.2 μm，270 mm×266 mm的方形是由45°的斜面延伸形成的，且45°斜面根部為R10的圓弧銜接過渡。立體圖如圖2所示。整體形狀偏大，如果采用傳統的銑圓弧方法加工，需要的刀具比較長，加長刀具有剛性低的缺點，不僅影響加工效率，還容易產生振刀現象，從而影響產品的表面質量。所以，只能采用參數編程，用短刀具進行快速的對大面積零件的切削，因此也增加了編程難度。

圖1

2.加工分析

由于零件結構形狀偏大，無法直接用銑圓弧編程方法來加工，所以采用參數編程，通過用微小直線段來逼近圓弧的形成。選用球頭銑刀，銑削順序如立體圖編號。零件表面粗糙度值要求Ra=3.2 μm，在編制程序中，把加工圓弧面旋轉步距記作繞圓弧圓心的旋轉角度，45°斜面的移動步距記作在任意一個坐標軸的每次走刀距離。以下是為保證Ra=3.2 μm表面粗糙度值的步距的計算方法:

圖2

圓弧面變化度數計算公式如下:

如圖3所示，A為變化的度數;Dr為球刀半徑;R為被加工圓弧半徑;H為表面粗糙度值。

圖3

其中:b=R+Hc=Dr+R;

a=Dr

45°斜面步距變化計算公式如下:

如圖4所示，P為變化的步距;Dr為球刀半徑;H為表面粗糙度值。

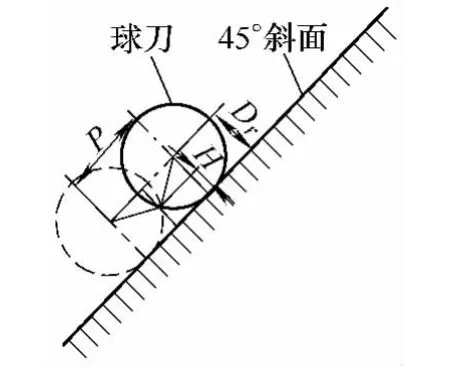
圖4

3.分析加工編程方法

結合圖1和圖2，現分別分析1、2、3、4各部分的編程方法和各個參數的計算關系式。

(1)第一部分加工的要素有:R1075，R10，45°，R1090，并且為對稱方向，所以另一個方向用鏡像功能。如圖5及放大圖B:R1075處X和Z的參數方程關系為:把起始角度8.24°到終點角度7.73°的角度變化記作α:

X=sinα × (1075+Dr)

Z=cosα × (1075+Dr)

Y為定值，Dr為球刀半徑 (下文同理)，R10處X和Z的參數方程關系為:

X=a－sinα× (10－Dr)

Z=b－cosα× (10－Dr)

Y為定值，45°斜面處X和Z的參數方程關系為把Z點的起點坐標到終點坐標的步距變化記作β:

X=a－tan45°×β+sin45°×Dr

Z=b+β+sin45°×Dr

Y為定值，R1090同理R1075的方程關系。

圖5

(2)第二部分加工的部位為R1075和R1075線條形成的R10和45°斜面。本部分只分析R10和45°的斜面。如圖6所示。分析得知，R10和45°斜面的形成分別是R1075線條沿著R10和45°做的軌跡，因此在編程時，要考慮圓弧半徑由小到大的變化。再者，由兩點和半徑可做出一個圓弧的道理并結合圖5得知，在圓弧半徑變化的同時，當前半徑的起點和終點也在變化。

R10處的參數方程關系為:

R=1075+10－cosα × (10－Dr)

X起點 (終點)=165;定值

圖6

45°斜面處的參數方程關系為:

R=1077.93+β+cos45°×Dr

X起點 (終點)=165;定值

(3)第三部分加工的是零件底面，屬于內圓弧，在處理該部分參數關系式時，和外圓弧不同之處是外圓弧是圓弧半徑加球刀半徑，內圓弧是圓弧半徑減球刀半徑，其余都相同。

4.結語

參數編程是通過分析圖形結構，找出一個變化的要素，并且該要素能影響其他要素的形成，最主要的是要找準變化要素和被變化要素之間的關系式，才能確定整個零件的形成。該件就是采用參數編程，在保證粗糙度的前提下，用多個微小的直線段逼近成整個零件，采用該方法可以加工形狀類似、尺寸無論多大的產品零件，有效地節約了后續產品的再次加工的編程時間。