三類方程在微積分中若干典型應用

嚴 慧，徐立峰

(湖北師范學院 數學與統計學院， 湖北 黃石 435002)

三類方程在微積分中若干典型應用

嚴 慧，徐立峰

(湖北師范學院 數學與統計學院， 湖北 黃石 435002)

討論以代數方程、微分方程、函數方法、差分方程為工具，解決微積分中的各類常見問題的典型方法，內容包括極限、定積分、重積分、變限積分、級數的展開與求和，輔助函數的構造等各方面的常見題型。在[1]中我們討論了代數方程，微分方程的應用，在此我們將著重討論函數方程，差分方程及微分方程在更廣泛的問題中的典型應用.

微積分；微分方程；差分方程；函數方程

方程是我們解決各類實際問題最重要的工具．在中國古代，即已出現用不定方程求解“雞兔同籠”等問題，15世紀意大利數學家以求解高次方程相互挑戰而風靡一時．在現代，隨機微分方程、偏微分方程、抽象空間中的微分方程等仍是現代數學中最具挑戰性的領域．因而在我們的數學教學中，從最基礎的教學開始，就注意訓練學生逐步掌握好這一工具是我們數學教學中一個有意義的課題．方程體系龐大，理論深邃，但本文的目的是訓練學生有效地掌握這一工具，并不涉及方程的理論，因而我們把所用到的知識限制在經濟類高等數學知識范疇(即所謂數學三)，例如高教版中國人民大學朱來義主編的《微積分》．

本文的寫法：用各類實例介紹用建立方程的技巧解決微積分中的各類問題，如極限、定積分、二重積分、變限積分、數項級數求和、冪級數求和函數、函數的冪級數展開、中值問題中輔助函數的構造等．以使學生在盡可能廣泛的知識領域中受到訓練，使學生在各種形式不同的問題中，有意識地自覺運用各類方程這一數學工具．為說明方法的代表性，我們大部分例子選自碩士研究生入學考試試題，我們將予以標注，例如“99年數學三”，即指1999年全國碩士研究生入學考試數學三試題．

由于本文的目的在于增強學生分析問題的能力，因此我們重在對解題思路的分析，而略去了解題的過程．

1 實例與分析

在文[1]中我們討論了代數方程、微分方程的應用．本文是[1]的繼續，將討論函數方程、差分方程的應用，然后討論微分方程在中值問題、函數零點唯一性問題、某些極限問題中構造輔助函數方面的應用．

首先我們討論冪級數中方程方法的應用，實際上在高中數學中已有這樣的技巧，但那是將問題轉化為代數方程，而在[1]中我們將問題轉化為一個微分方程，而在有些場合我們則需要構建函數方程或差分方程．

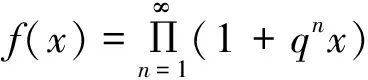
f(x)=(1+qx)(1+q2x)……(1+qnx)…

(1)

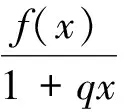
(2)

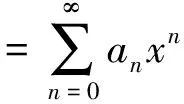
a0+(a1q+a0q)x+(a2q2+a1q2)x2+…+(anqn+an-1qn)xn+…

(3)

對比系數得anqn+an-1qn=an，于是得到遞推式

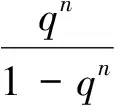
(4)

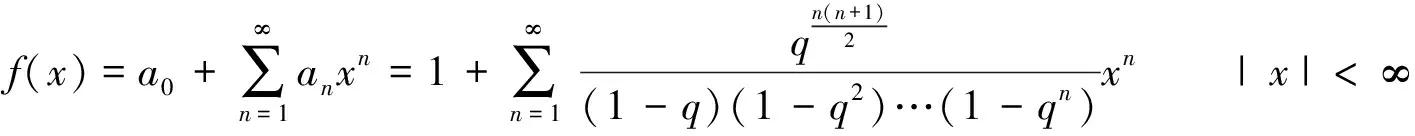
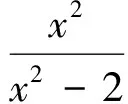
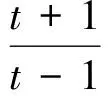
微分方程的離散化即成為差分方程，如果說積分和函數的極限問題常將微分方程作為工具的話，那么作為類比級數，數列的許多問題常以差分方程作為工具．但遺憾的是盡管差分方程已納入教學內容，但這方面不僅是學生的短板，在我們的教學與參考書籍中這方面的論述也很少．

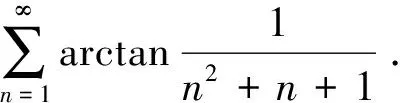
分析 這是課本[1]中原題，課本有如下提示：

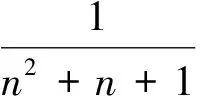
這種方法需較高的技巧。如將它轉化為一個差分方程的問題，則從思想方法上看，會簡單許多。借助裂項法的思路構造差分方程：

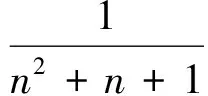
(5)

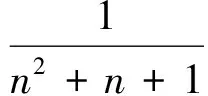
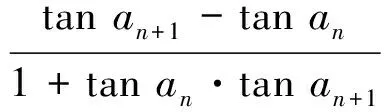
遞推數列極限的證明與計算是微積分中的一類典型問題，而遞推數列本身就是一類差分方程，差分方程的求解方法自然也就成為解決這類問題的工具．

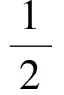
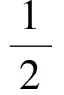
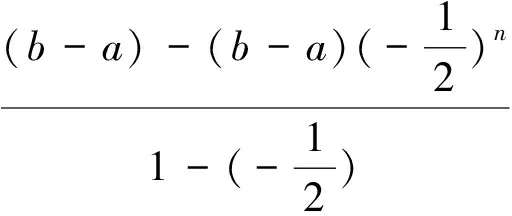
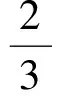
微分中值定理被稱為微分學基本定理，微分學大部分應用直接或間接地依賴于中值定理，因此中值定理的應用技巧被視為微積分教學與各類考試的重點也就是理所應當的了．而中值定理應用中的主要技巧就是輔助函數的構造.微分方程則是構造輔助基本的工具．

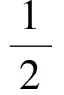
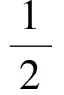
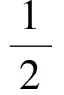
問題(2)的關鍵在于構造輔助函數，使f′(ξ)-λ[f(ξ)-ξ]-1 的零點問題轉化為某一個函數F(x) 的導函數的零點問題．由結論f′(ξ)-λ[f(ξ)-ξ]-1 =0 ，可構造微分方程f′(x)-λf(x)=1-λx，由求解公式得f(x)=eλx(xe-λx+c)(c為任意常數)分離常數c=[f(x)-x]e-λx，故構造輔助函數F(x)=e-λx[f(x)-x]，由于F(0)=0,F(η)=0 在[0,η] 上使用羅爾定理，存在ξ∈(0,η) 使F′(ξ)=0，即e-λξ[f′(ξ)-λ(f(ξ)-ξ)-1]=0，但e-λξ≠0，故f′(ξ)-λ[f(ξ)-ξ]=1 ．

輔助函數常常能使條件或結論更為集中，因此例5中構造輔助函數的方法不僅適用于中值問題，也適合于微積分中的其它各類問題．

例6 設f(x) 在R上可導，且f(x)+f′(x)>0 .試證：f(x)使至多只有一個零點．

分析 通常的思路是希望證得f′(x)>0 ，但這并不容易從條件中獲得，考慮構造輔助函數使條件更為集中．

先構造微分方程f(x)+f′(x)=0 ，解得f(x)=ce-x分離常量，c=exf(x)

故構造輔助函數F(x)=exf(x) ，由條件F′(x)=ex[f′(x)+f(x)]>0，故F(x)嚴格單調增加，F(x)至多只有一個零點，但ex無零點，于是f(x)至多只有一個零點．

2 結束語

由于篇幅所限，微積分又涉及如此龐大的體系，本文中的內容僅是九牛一毛而已，我們做這一專題討論是希望更進一步豐富課堂教學的內容，使學生能主動自覺地運用方程這一工具解決各種數學問題，我們相信經過不斷地研究、總結必能大大提高學生解題能力．并為今后運用它解決現實世界中各種實際問題打下了堅實的基礎，而這也正是我們數學教學的目的所在．

在第1部分中，我們使用了代數方程、微積分方程、函數方程、差分方程作為我們的解題工具，在應用中應仔細研究，捉摸各種應用場合的特點，作為本文的結束，我們再給出一個反例，其錯誤原因就在于混淆了不同類的方程，這也是初學者易犯的一個典型錯誤．

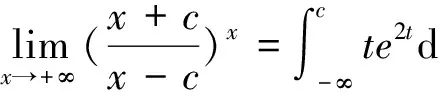
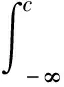
(6)

方程(6)兩端對c求導得2e2c=ce2c，故c=2 ．

上述解法的錯誤就在于把(6)當作微分方程(積分方程)而(6)實際上是一個代數方程，其中c并不是自變量，而是一個特定的數值，不能兩端求導，否則就如x=1 兩端求導而得到 1=0這樣荒謬的結果了．

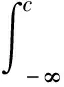
[1]嚴慧.方程在微積分中的應用[J]．湖北師范學院學報(自然科學版)，2011，31(3):115～118.

[2]朱來義.微積分(第三版)[M]．北京：高等教育出版社，2009.

[3]同濟大學數學系.高等數學(第五版)[M]．北京：高等教育出版社，2002.

[4]胡適耕，姚云飛.數學分析——定理·問題·方法[M]．北京：科學出版社，2007.

[5]華東師范大學數學系.數學分析(上、下冊)[M]．北京：高等教育出版社，2001.

[6]李永樂，劉西垣，袁蔭棠.數學(三)歷年試題解析[M]．北京：國家行政學院出版社，2009.

Ontheapplicationoffunctionequations,differenceequationsanddifferentialequationsindifferential-integralcalculus

YAN Hui, XU Li-feng

(Collage of Mathematics and Statistics, Hubei Normal University,Huangshi 435002,China)

In this paper, we discuss the methods to solve the problems in differential-integral calculus by the using of algebraic equations. The content include the limit, definite integral, multiple integral, variable limit of integral, series and the construction of auxiliary function.

differential-integral calculus; differential equation; difference equation; function equation

2014—04—03

湖北省教育廳資助項目(Q20122202)

嚴慧，女，湖北黃梅人，講師，碩士，主要從事概率論與數理統計研究.

O172.2

A

1009-2714(2014)03- 0100- 04

10.3969/j.issn.1009-2714.2014.03.023