一類具有非線性收獲率的捕食者-食餌生態經濟系統的分支分析
劉唯一,傅朝金,陳靜,柯于勝
(1.咸寧職業技術學院 機電工程系,湖北 咸寧 437100;2.湖北師范學院 數學與統計學院,湖北 黃石 435002)
一類具有非線性收獲率的捕食者-食餌生態經濟系統的分支分析
劉唯一1,2,傅朝金2,陳靜2,柯于勝2
(1.咸寧職業技術學院 機電工程系,湖北 咸寧 437100;2.湖北師范學院 數學與統計學院,湖北 黃石 435002)
研究了一類捕食者-食餌生態經濟模型的動力學行為.該模型具有非線性收獲率,這使得模型更具一般性.選取經濟利潤v作為分支參數,通過局部參數化方法,Hopf分支理論和形式級數方法研究了系統的Hopf分支.同時,改進的參數化計算過程更簡單,能夠處理更復雜的模型.最后,通過MATLAB仿真證明了我們的結果.
微分代數方程;穩定性;Hopf分支;非線性收獲率;改進的算法
0 引言
近年來,捕食者-食餌生態經濟系統受到數學工作者的廣泛關注和深入研究.文獻[1~4]研究了建立在微分方程基礎上具有人為收獲的捕食者-食餌系統,得到了復雜的動力學行為,如平衡點的穩定性[1~3],Hopf分支[2],Bogdanov-Takens分支[3],極限環[1,3,4]等.文獻[5~8]給出了基于微分代數方程的捕食者-食餌生態經濟系統,系統地研究了奇異誘導分支[6],狀態反饋控制[6],鞍結分支[6~8]等.文獻[9~11]研究了具有線性收獲率的捕食者-食餌生態經濟系統的中心穩定性和Hopf分支.然而,線性收獲率只是一種理想化的情形.本文研究一類具有非線性收獲率的系統,模型如(1)式
(1)

內討論系統(1).
本文將對系統(1)進行定性研究,以經濟利潤v作為分支參數,通過參數化方法,Hopf分支理論和形式級數方法討論系統的Hopf分支,然后通過MATLAB數值模擬驗證結果的正確性和合理性。
1 Hopf分支分析
為了方便,令
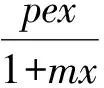
對于系統(1),易求得平衡點為
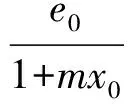
在文獻[9~11]中,作者均對原系統作了一個線性變換,轉而去分析變換后系統,事實上這是多余的,而且會導致后面的計算量增大.如果模型比較復雜,則很難計算出結果.所以我們去掉了這一過程而直接分析系統(1).
現考慮如下所定義的系統(1)的局部參數化Ψ:
X=Ψ(v,Y)=X0(v)+U0Y+V0h(v,Y),g(v,Ψ(v,Y))=0
其中
h:2→是一個光滑映射.于是(1)的參數化系統為
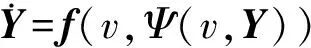
即
(2)
關于上述參數化系統(2)的詳細定義可參見文獻[12].系統(1)的正平衡點X0對應于參數化系統(2)的平衡點Y=0,參數化系統(2)在平衡點Y=0 處的特征方程為
λ2+a1(v)λ+a2(v)=0
(3)
其中
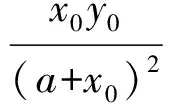
如果方程(3)存在零實部的特征根,系統(1)將會發生Hopf分支.
現在我們選擇經濟利潤v作為分支參數來研究系統(1)的Hopf分支.在方程(3)中,令a1(v)=0,得分支值v0,滿足
事實上,如果令a12(v)<4a2(v) ,方程(3)有一對共軛根:


為了計算Hopf分支,根據文獻[12,13],當v=v0,X=X0時,需要求出系統(1)的如下標準型
(4)

可以證明參數化系統(2)當v=v0,X=X0時可寫為
(5)
由鏈式法則可求得
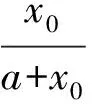
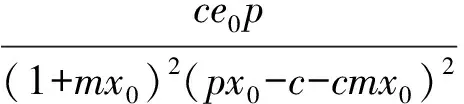
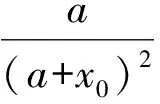




f2y1y2y2(v0,X0)=0f2y2y2y2(v0,X0)=0
對比(5)和(4),現對(5)進行如下非奇異線性變換
這樣就求出了標準型(4)的全部非零系數,其中



根據Hopf分支理論[13],需要計算16σ0的值.
由上面的結果,有如下定理
定理1 對系統(1),存在一個正常數ε和正平衡點X0(v)的兩個充分小的鄰域O,P,其中0<ε?1,O?P.
情形1:如果16σ0>0,那么
1) 當v0 情形2:如果 16σ0<0,那么 1) 當v0-ε 例 我們取系統(1)的系數如下 a=0.5,b=2,d=2,r=1,p=4,c=1,k=2,m=0.1 于是系統(1)為 (6) 容易求得正平衡點為X0=(0.5000000,0.6779619,0.3381400)T,分支值為v0=0.30594 .由定理1,當v 在圖1中,系統(6)的平衡點X0(v) 是局部漸近穩定的.在圖2中,系統(6)在X0(v) 處產生一個周期軌道.在圖3中,系統(6)的平衡點X0(v) 是不穩定的. 圖1 當初值為x0=0.499 ,y0=0.666,e0=0.333 ,經濟利潤v=0.27999 圖2 當初值為x0=0.499,y0=0.666,e0=0.333,經濟利潤v=0.30590 圖3 當初值為x0=0.499,y0=0.666,e0=0.333,經濟利潤v=0.31890>v0時的Hopf分支圖 [1]Gakkhar S,Singh B.The dynamics of a food web consisiting of two preys and a harvesting predator [J].Chaos,Solitons and Fractals,2007,34(4):1346~1356. [2]Kar T K,Pahari U K.Modeling and analysis of a prey-predator system with stage structure and harvesting [J].Nonlinear Analysis: Real World Applications,2007,8(2):601~609. [3]Xiao Dongmei,Li Wenxia,Han Maoan.Dynamics in ratio-dependent predator-prey model with predator harvesting [J].Journal of Mathematical Analysis and Applications,2006,324(1):14~29. [4]Yang Kuang,Feedman H I.Uniqueness of limit cycle in cause-type predator-prey systems [J].Mathematical Biosciences,1988,88(1):67~84. [5]Liu Chao,Zhang Qingling,Duan Xiaodong.Dynamical behavior in a harvested differential-algebraic prey-predator model with discrete time delay and stage structure [J].Journal of the Franklin Institute,2009,346(10):1038~1059. [6]張 悅,張慶靈,趙立純.階段結構廣義生物經濟模型的分岔及控制 [J].系統工程學報,2007,22(3):11~16. [7]張 悅,張慶靈.基于廣義生物經濟系統的混沌控制 [J].控制與決策,2007,22 (4):445~448. [8]Zhang Xue,Zhang Qingling,Zhang Yue.Bifurcations of a class of singular biological economic models [J].Chaos,Solitons and Fractals,2009,40(3):1309~1318. [9]Liu Wei,Fu Chaojin,Chen Boshan.Hopf bifurcation for a predator-prey biological economic system with Holling typeⅡ functional response [J].Journal of the Franklin Institute,2011,348(6):1114~1127. [10]Liu Wei,Fu Chaojin,Chen Boshan.Hopf bifurcation and center stability for a predator-prey biological economic model with prey harvesting [J].Communications in Nonlinear Science and Numerical Simulation,2012,17(10):3989~3998. [11]Zhang Guodong,Zhu Lulu,Chen Boshan.Hopf bifurcation and stability for a differential-algebraic biological economic system [J].Applied Mathematics and Computation,2010,217(1):330~338. [12]陳伯山,廖曉昕.微分代數系統的標準型和分支 [J].應用數學學報,2000,23(3):429~443. [13]Guckenheimer J,Holmes P.Nonlinear Oscillations,Dynamical Systems,and Bifurcations of Vector Fields [M].New York:Springer-Verlag,1983. Bifurcationanalysisofapredator-preybiologicaleconomicsystemwithnonlinearharvestingrate LIU Wei-yi1,2,FU Chao-jin2,CHEN Jing2,KE Yu-sheng2 (1.Department of Mechanical and Electrical Engineering,Xianning Vocational Technical College,Xianning 437100,China;2.College of Mathematics and Statistics,Hubei Normal University,Huangshi 435002,China) In this paper,we analyze a biological economic system with harvesting effort on prey.Different from previous researchers' models,this model with nonlinear harvesting rate is more general.By employing local parameterization method,Hopf bifurcation theory and the formal series method,the Hopf bifurcation of the proposed system is investigated.Here we choose economic revenue as a positive bifurcation parameter.And the improved calculation process of parameterization is much more simple and it can handle more complex models which could not be dealt with by previous algorithms due to extensive calculation.Finally,by MATLAB simulation,the validity and feasibility of obtained results are illustrated. differential-algebraic equations;stability;Hopf bifurcation;nonlinear harvesting rate;improved algorithm 2013—12—11 劉唯一(1979— ),男,湖北黃石人,碩士研究生,主要研究方向為微分方程與控制論. O193 A 1009-2714(2014)02- 0046- 06 10.3969/j.issn.1009-2714.2014.02.011

2 數值仿真