基于自回歸法的滑坡監測數據Kalman濾波的應用

徐愛功,張建龍,隋 心,劉 偉,張兆南

(1.遼寧工程技術大學 測繪與地理科學學院，遼寧 阜新 123000；2.洛陽電子裝備試驗中心，河南 洛陽 471000；3.東北煤田地質局物探測量隊，遼寧 沈陽 110101)

(1.School of Geomatics, Liaoning Technical University, Fuxin 123000, China; 2.Luoyang Electronic Equipment Test Center, Luoyang 471000, China; 3.Physical Exploration and Surveying Team, Northeast Coalfield Geology Bureau, Shenyang 110101, China)

基于自回歸法的滑坡監測數據Kalman濾波的應用

徐愛功1,張建龍1,隋 心1,劉 偉2,張兆南3

(1.遼寧工程技術大學 測繪與地理科學學院，遼寧 阜新 123000；2.洛陽電子裝備試驗中心，河南 洛陽 471000；3.東北煤田地質局物探測量隊，遼寧 沈陽 110101)

介紹了卡爾曼濾波的基本模型，針對運動學方法以監測點位置參數、速率參數為狀態向量，以加速度為噪聲向量建立觀測方程和狀態方程的過程比較復雜。把自回歸法引入狀態方程和觀測方程的建立中，并結合某露天礦滑坡動態監測數據分析了模型的應用。結果表明，濾波值和觀測值之間差值保持在1～3 cm之間，濾波后圖像較原觀測值圖像更為光滑，表明所建模型是合適的，能夠反映滑坡動態變化過程，從而為礦滑坡監測預報提供數學工具。

自回歸模型；卡爾曼濾波；滑坡；預報

我國露天礦數量眾多，高陡邊坡穩定性一直是影響露天礦生產安全的重要問題。據統計，不穩定邊坡或具有潛在滑坡危險的邊坡占邊坡總長度可達15%～20%，甚至更高[1]。由于滑坡具有時間上的突發性和后果上的嚴重性，因而加強對滑坡體的監測，對滑坡作短期、中期和長期預報，具有重要的現實意義[2]。

Kalman濾波是美籍匈牙利數學家卡爾曼在濾波理論中引入狀態空間分析方法提出的一種處理動態數據的方法，是一種線性無偏且以均方誤差最小為準則的最優估計算法,由于其具有可遞推實現，利于計算機運算等優點，已成為目前處理動態觀測數據的一種常用方法。滑坡是一個動態發展過程，適合采用卡爾曼濾波處理觀測數據，并作出預報。文獻[3-6]在建立濾波模型時以監測點的位置、速率和加速度等參數構建狀態向量、觀測向量，這種方法能夠反映變形體的運動狀態，但是構造過程較為復雜。本文將監測點高程變化看做是一個依賴于時間的變量，監測前后各期之間具有一定的相關性，利用自回歸法建立卡爾曼濾波的狀態方程和觀測方程，并在某露天礦滑坡動態數據處理中的應用做了研究。

1 Kalman濾波模型

1.1 Kalman濾波模型的建立

Kalman濾波方程的建立，需要已知系統模型和觀測模型，并且要給出噪聲的先驗統計性質，以及系統狀態的初始值。進而根據建立的方程實時獲得系統的狀態變量和輸入信號的最優估值。下面給出離散Kalman濾波模型的建立過程[7]：

狀態方程xk=Φk,k-1xk-1+Γk,k-1ωk-1.

(1)

觀測方程zk=Hkxk+vk.

(2)

式中:Φk,k-1為狀態轉移矩陣；Γk,k-1為狀態噪聲系數陣；Hk為觀測向量系數陣；ωk-1,vk分別表示狀態噪聲與觀測噪聲，且具有如下統計特性：

E(ωk-1)，E(vk)為ωk-1，vk的期望；Rωω(k,j)，Rvv(k,j)為ωk，vk的自協方差；Rωv(k,j)為ωk，vk的互協方差；E(x0)，var(x0)為已知的初值；R(x0,ωk-1)，R(x0,vk)為x0與ωk-1和vk的協方差。由于動態噪聲和觀測噪聲均是零均值的白噪聲序列，且互不相關,故以上建立的模型可以稱為完全不相關的白噪聲作用下的Kalman濾波。在滿足均方誤差最小的前提下可以得出以下濾波遞推公式[7]：

狀態估計校正

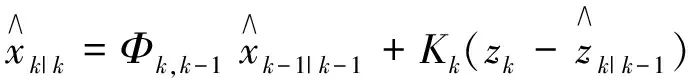
(3)

卡爾曼增益

(4)

誤差協方差預測

(5)

誤差協方差估計校正

Pk|k=(I-KkHk)Pk|k-1.

(6)

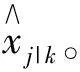
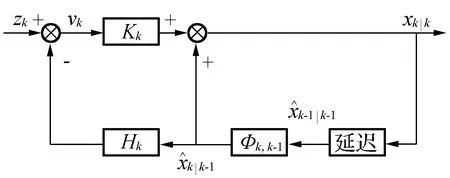
圖1 卡爾曼濾波示意圖

1.2 狀態方程和觀測方程的建立

在處理滑坡監測數據時，狀態方程和觀測方程的建立是關鍵的一步，盡管Kalman濾波模型狀態方程和觀測方程的建立方法很多，但多數文獻是以監測點的運動學模型為基礎建立的。例如，文獻[3-5]是以監測點的位置參數(水平坐標和高程)及三維坐標速率作為狀態向量，以三維坐標加速度為噪聲向量建立的。文獻[6]將某時刻變形量對上一時刻展開成泰勒級數取至三次方，仍然是采用運動學模型。該方法能夠反映變形體的運動狀態，但方程建立過程較為復雜。本文采用一種較為簡單的方法建立狀態方程和觀測方程，即自回歸法，避免了計算點位變化過程的速度和加速度，建立過程如下：

自回歸模型

xk=η1xk-1+η2xk-2+…+ηnxk-n+ωk-1.

(7)

η1,η2,…,ηn是n階加權系數，ωk-1是白噪聲序列[8]，將該模型引入Kalman濾波中。

令x1(k)=xk，x2(k)=xk-1…

xi(k)=xk-i+1，xn(k)=xk-n+1.

則狀態方程為

即xk+1=Φk+1,kxk+Γk+1,kωk.

其中:

觀測方程為

zk+1=[1 0 … 0]·[x1(k+1)x2(k+1) …

xn(k+1)]T+v(k+1).

即zk+1=Hk+1xk+1+vk+1.

其中：Hk+1=[1 0 … 0]。

至此，就完成了狀態方程和觀測方程的建立。

這里，對加權系數ηi(i=1,2,…,n)的求法通常有矩估計法、最小二乘法、最小方差法、極大似然估計法等[8]，通常采用最小二乘法，將式(7)改寫成矩陣形式為

即V=Aη-L.

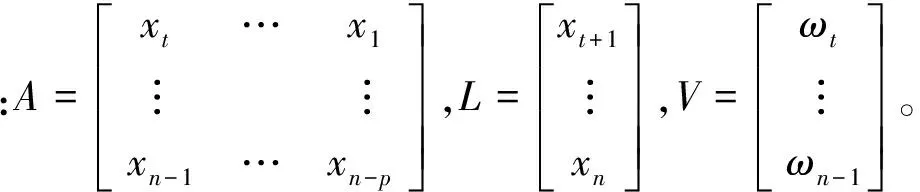
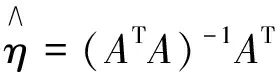
(8)

1.3 狀態初值的確定

卡爾曼濾波是由一組遞推公式給出的，在濾波前需要給定初值x0和P0。x0可以根據前面幾組觀測值給定，P0可以由初始測量值經過統計方式給出，通常P0應為對角陣[9]。

2 實例分析

2.1 概 況

阜新礦業集團白音華某露天礦位于內蒙古西烏珠穆沁旗境內，在不斷開挖過程中邊坡受采礦爆破影響強烈，加之大型機械作業震動及長期雨水侵蝕，以及不斷堆積擴大的排土場對滑坡體壓力不斷增大[10]，穩定性逐漸變差，最終導致滑坡的發生。

通過監測獲取的數據采用Kalman濾波模型處理。濾波模型是通過已知觀測值建立的，模型系數矩陣在模型確定的前提下即可得到。本文首先采用某監測點前30期的高程觀測值(見表1)求解自回歸方程，建立基于自回歸法的Kalman濾波模型，通過分析確定轉移矩陣及觀測矩陣，建立狀態方程和觀測方程。再對后面10期觀測數據進行濾波，檢驗模型的正確性及濾波效果。

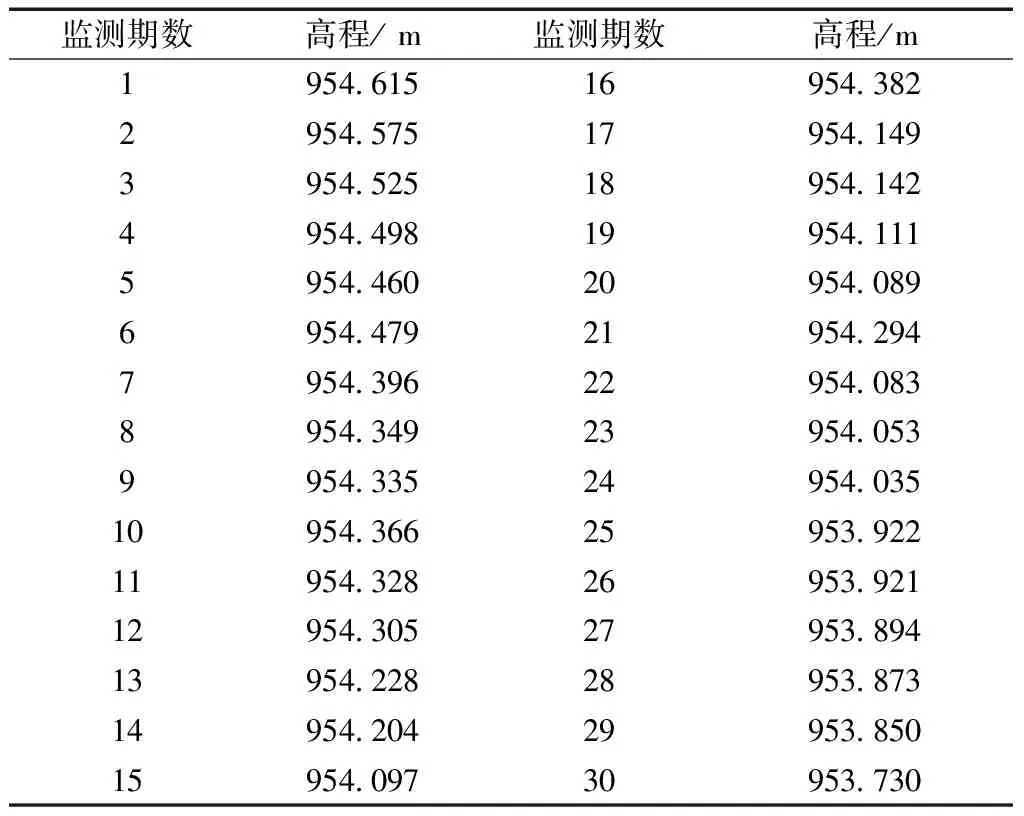
表1 某監測點各期觀測值高程

2.2 模型建立

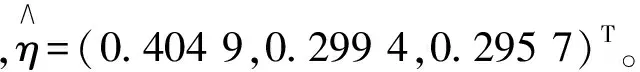
Γ=[1 0 0]T，H=[1 0 0].

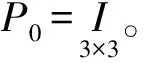
2.3 程序設計

由于Matlab具有變量定義簡單、編程效率高、作圖方便等優點[11]，故對上述建立的卡爾曼濾波采用Matlab進行程序設計，Kalman濾波程序如下：

clc;

close all;

z1=xlsread(′data.xls′,′sheet1′,′A1:A30′); %觀測值

p0=eye(3); %初值方差陣賦初值

p=p0;

phik=[0.4049,0.2994,0.2957;1,0,0;0,1,0]; %狀態轉移矩陣

Qk=eye(3); %狀態噪聲矩陣

Hk=[1,0,0]; %觀測向量系數矩陣

Rk=1; %觀測向量噪聲矩陣

x0=[954.615,954.575,954.525]′;

Xk=x0; %狀態矩陣賦初值

for k=1:30

Pk=phik*p*phik′+Qk; %誤差協方差

Kk=Pk* Hk′*inv(Hk*Pk*Hk′+Rk); %增益矩陣

Zk=z1(k);

Xk=phik*Xk+Kk*(Zk-Hk*phik*Xk); %最優估計值

x1(k)=Xk(1);

p=(eye(3)-Kk*Hk)*Pk; %誤差協方差估計校正

end

2.4 數據分析

由圖2、圖3可以看出濾波值和原始測量值保持一致的下降趨勢，且最大偏差為6.28 cm，是由于第16和21兩次觀測值可能含有較大誤差，大部分差值保持在1～4 cm。濾波后圖像比原測量曲線要平滑，說明模型建立的是合理的，能夠達到消除測量中干擾誤差的目的，經過預測、修正所得到的濾波最優估值能夠更好地反映滑坡動態變化過程。

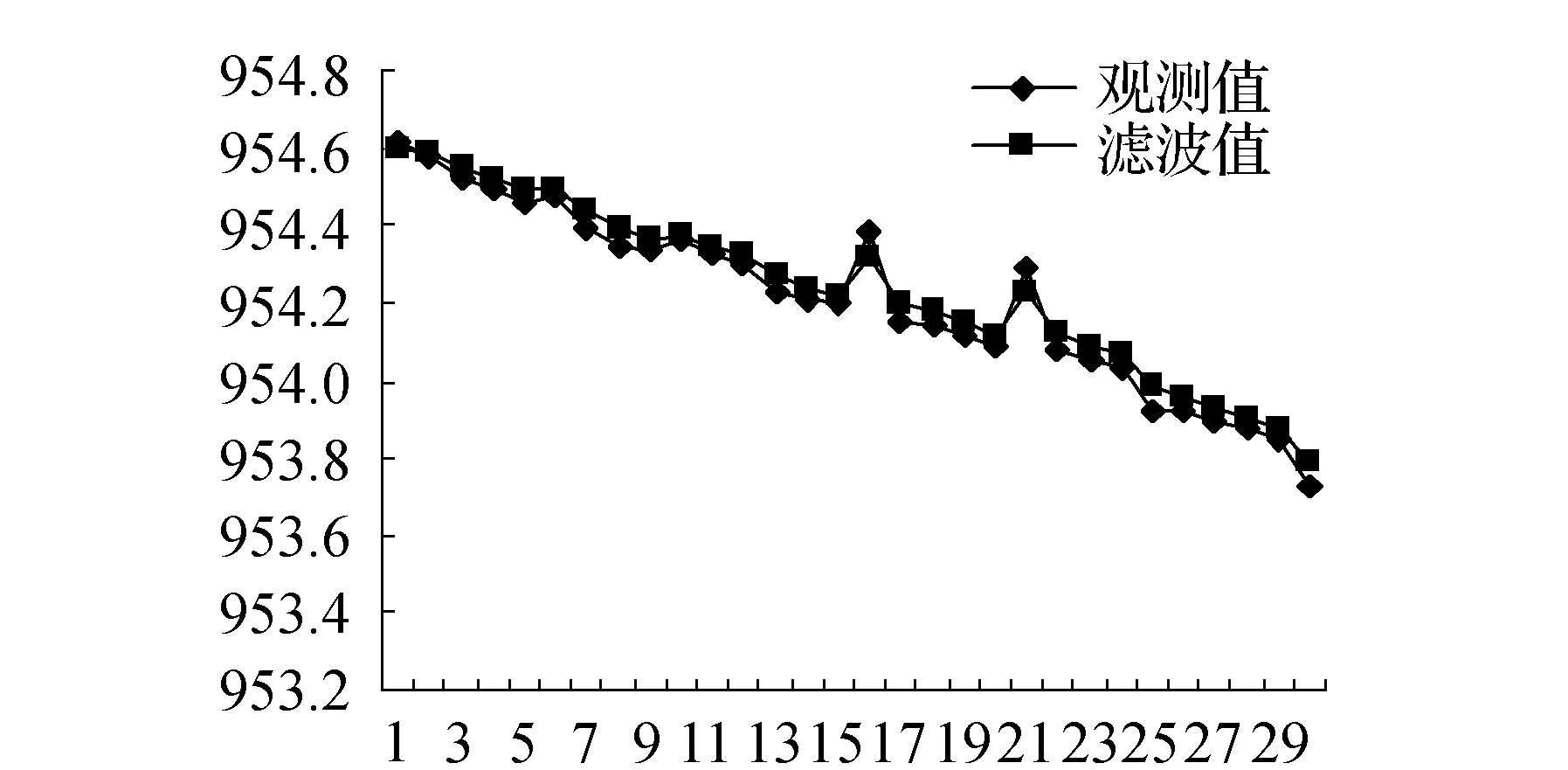
圖2 觀測值與濾波值對比

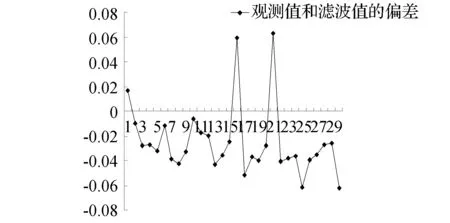
圖3 觀測值與濾波值的偏差

通過以上建立的濾波模型再對未來10期(31～40期)觀測數據做出預測，初值的確定采用以上數據最后3期，即x0=[953.873,953.850,953.730]。觀測值與估計值如表2所示。觀測值與估計值對比和差值如圖4、圖5所示。可以看出，僅預測初始2期偏差較大，這是由于遞推過程初始值選取與實際觀測值之間有一定的偏差造成的，之后幾期偏差都在1～3 cm，說明初值的選取僅會影響前面較少幾期的預測結果，而不會對之后幾期有影響；濾波估計值呈一致的下降趨勢，而原始觀測值由于存在觀測誤差并沒有呈一致下降趨勢，說明濾波后能夠較好反映滑坡動態發展規律，濾波對滑坡的預測效果良好。

表2 未來10期高程觀測值與估計值對照

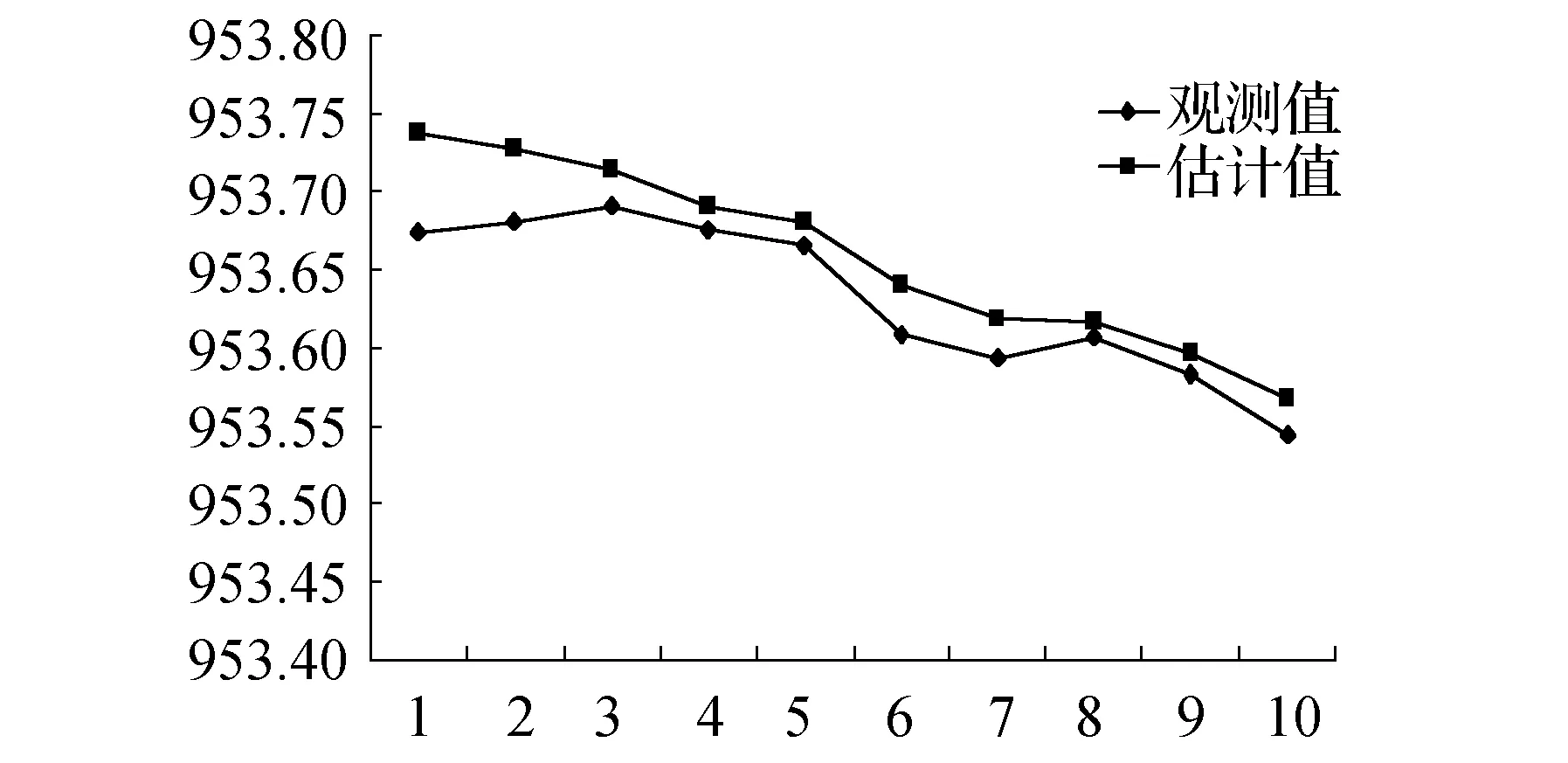
圖4 未來10期觀測值與估計值對比

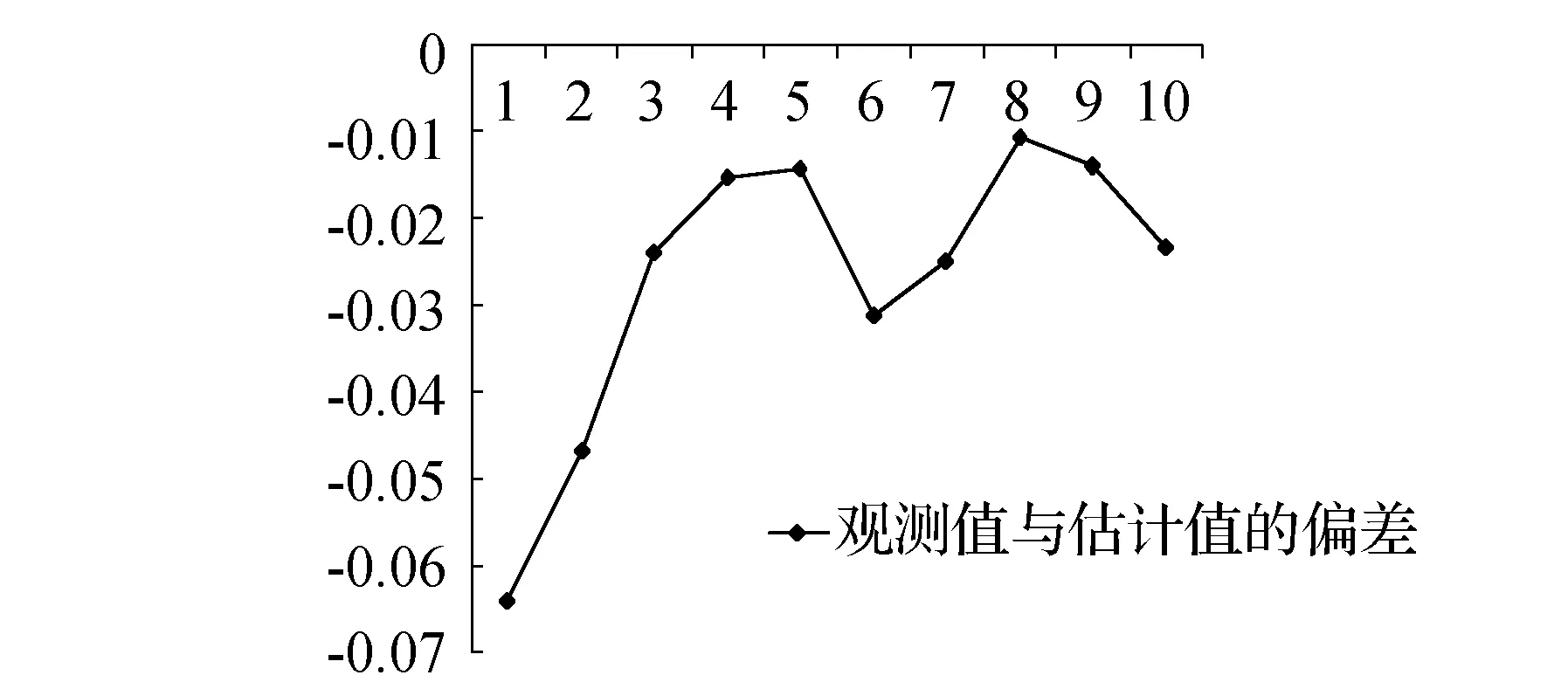
圖5 未來10期觀測值與估計值的差值

3 結 論

通過以上模型的建立及數據處理結果分析可以得出以下結論：

1)將自回歸法引入狀態方程和觀測方程的建立過程中，使得濾波模型的建立過程簡單化，避免采用運動學方法的復雜性。

2)Kalman濾波把參數的估計和預報結合起來，有效消除觀測噪聲，通過參數的不斷修正，增強模型適應不斷獲得的數據，可以實時計算濾波值，也可以對未來幾期做出預測，為預測滑坡的變形發展提供依據。

3)如果觀測不平穩，一些觀測值有較大起伏或觀測值含有較大誤差，濾波偏差會較大；初值選取與實際觀測值有一定偏差時，預報結果前面較少幾期偏差會較大，所以應用Kalman濾波也是有一定的局限性。

[1]姚潁康，周傳波，郭廖武，等.深凹露天礦山巖質邊坡穩定性預測[J].金屬礦山，2008(3):42-45.

[2]張正祿，黃全義，文鴻雁，等.工程的變形監測分析與預報[M].北京：測繪出版社，2007.

[3]高雅萍，馮曉亮.GPS變形監測動態數據處理中卡爾曼濾波的應用[J].海洋測繪，2006,26(4)：36-38.

[4]許國輝，余春林.卡爾曼濾波模型的建立及其在施工變形測量中的應用[J].測繪通報，2004(4):22-23.

[5]陳帥，趙麗，李超，等.卡爾曼濾波在壩體變形監測中的應用[J].全球定位系統，2011(5):83-84.

[6]陸付民，王尚慶，李勁.離散卡爾曼濾波法在滑坡變形預測中的應用[J].水利水電科技進展，2009,29(4):6-9.

[7]劉勝，張紅梅.最優估計理論[M].北京：科學出版社，2011：129-164.

[8]張樹京，齊立心.時間序列簡明教程[M].北京：清華大學出版社，北方交通大學出版社，2003：49-54.

[9]修延霞，候凱.卡爾曼濾波在大壩變形監測中的應用[J].城市勘測，2010(1):92-94.

[10]溫德娟，滕壽仁，楊子榮.白音華3號露天礦礦坑充水因素研究[J].煤炭技術，2006,25(7):97-98.

[11]劉衛國.Matlab程序設計教程[M].2版.北京：中國水利水電出版社，2010.

[責任編輯：劉文霞]

Application of Kalman filtering to the landslide monitoring data procession based on auto-regression method

XU Ai-gong1， ZHANG Jian-long1， SUI Xin1， LIU Wei2， ZHANG Zhao-nan3

It introduces a basic model of Kalman filtering.The kinematic method establishes the observation equation and state equation based on location parameters and rate as the state vector, acceleration as the noise vector.The auto-regression method is introduced into the establishment of the state equation and observation equation, simply compared with the kinematic method.Taking one opencast mine landslide dynamic monitoring data as an example, it analyzes the model application.The results show that the deviation of filtering value and observed value is between 1 to 3cm, and the filtering image is smoother than the original observation image.It shows that the model is appropriate, and it can reflect the dynamic change process of landslide.So the method provides a powerful mathematical tool for this opencast mine landslide monitoring and prediction.

auto-regression method; Kalman filtering; landslide; forecast

2013-08-30

精密工程與工業測量國家測繪地理信息局重點實驗室開放基金資助項目(PF2012-8)；現代城市測繪國家測繪地理信息局重點實驗室開放課題資助項目(20111203W)

徐愛功(1963-)，男，教授，博士生導師.

P642

：A

：1006-7949(2014)09-0052-04

(1.School of Geomatics, Liaoning Technical University, Fuxin 123000, China; 2.Luoyang Electronic Equipment Test Center, Luoyang 471000, China; 3.Physical Exploration and Surveying Team, Northeast Coalfield Geology Bureau, Shenyang 110101, China)