柔性濾波驅動機構的自適應動態面模糊控制

羅紹華，王家序，李俊陽，石珍

(1.重慶大學 機械傳動國家重點實驗室，重慶400044;2.湖南文理學院 機械工程學院，湖南 常德415000)

柔性濾波驅動機構［1-2］將具有可控界面彈性變形的濾波減速器組件、伺服電機與傳感器集成一體，具有參數未知、非線性、強耦合和多變量等特征，其機械結構上的彈性體產生彈性預緊來補償齒側間隙與回差。柔性濾波驅動機構工作時，受到柔性變形、摩擦及傳動誤差等非線性因素的影響，這些因素將嚴重影響系統的控制精度、穩定性以及動態響應。國內外對考慮諸多非線性項的柔性濾波驅動機構的控制研究較少，因此，研究其先進的控制策略進而改善動靜態性能具有重要的理論研究意義和工程應用價值。

LuGre模型［3-4］能全面描述摩擦力的動靜態特性，但該模型參數會隨著外界條件諸如機械磨損、溫度和潤滑條件等因素而變化。由于時變特性，其摩擦補償控制已成為理論和應用研究的熱點。有些學者應用神經網絡［5］與模糊控制方法［6-7］辨識未知摩擦力。Seyfferth等［8］提出了柔性關節機器人的非線性諧波傳動模型，然而模型中更多考慮磁滯的可塑性。MingChih等［9］針對時變不確定性柔性關節機器人提出魯棒自適應控制器解決跟蹤問題。Yong-ming等［10］研究了基于反步法的直流電機驅動單關節柔性機器人自適應模糊輸出反饋控制問題，但未考慮非線性因素。劉金琨［11］針對單連桿柔性關節機器人控制系統設計了反步控制技術，但虛擬項多次微分產生所謂“系數膨脹”問題。動態面［12-13］設計過程中增加n-1個低通濾波器，克服反步法的不足。文獻［14］將動態面與神經網絡控制相結合，針對具有任意不確定性的嚴格反饋三角形SISO系統，提出了一種新的控制方法。本文針對柔性濾波驅動機構的控制問題，考慮非線性項的影響，設計了自適應動態面模糊控制器，驗證了系統的有效性和優越性。

1 柔性濾波驅動機構

1.1 系統結構

如圖1所示，柔性濾波驅動機構包括濾波減速器組件、伺服電機及傳感器。與傳統剛性齒輪相對，柔性濾波齒輪具有可控界面彈性變形，即采用多層材料復合設計齒輪本體，在設計的傳動精度范圍內在外齒輪本體鑲嵌一層彈性材料，彈性體產生變形量進行彈性預緊，從而自動補償齒側間隙與回差，有效防止極端工況與特殊環境的影響而產生的非線性耦合振動，避免發生“卡澀”甚至“卡死”等可靠性問題，保證傳動件在所設計的傳動精度和承載能力范圍內工作。

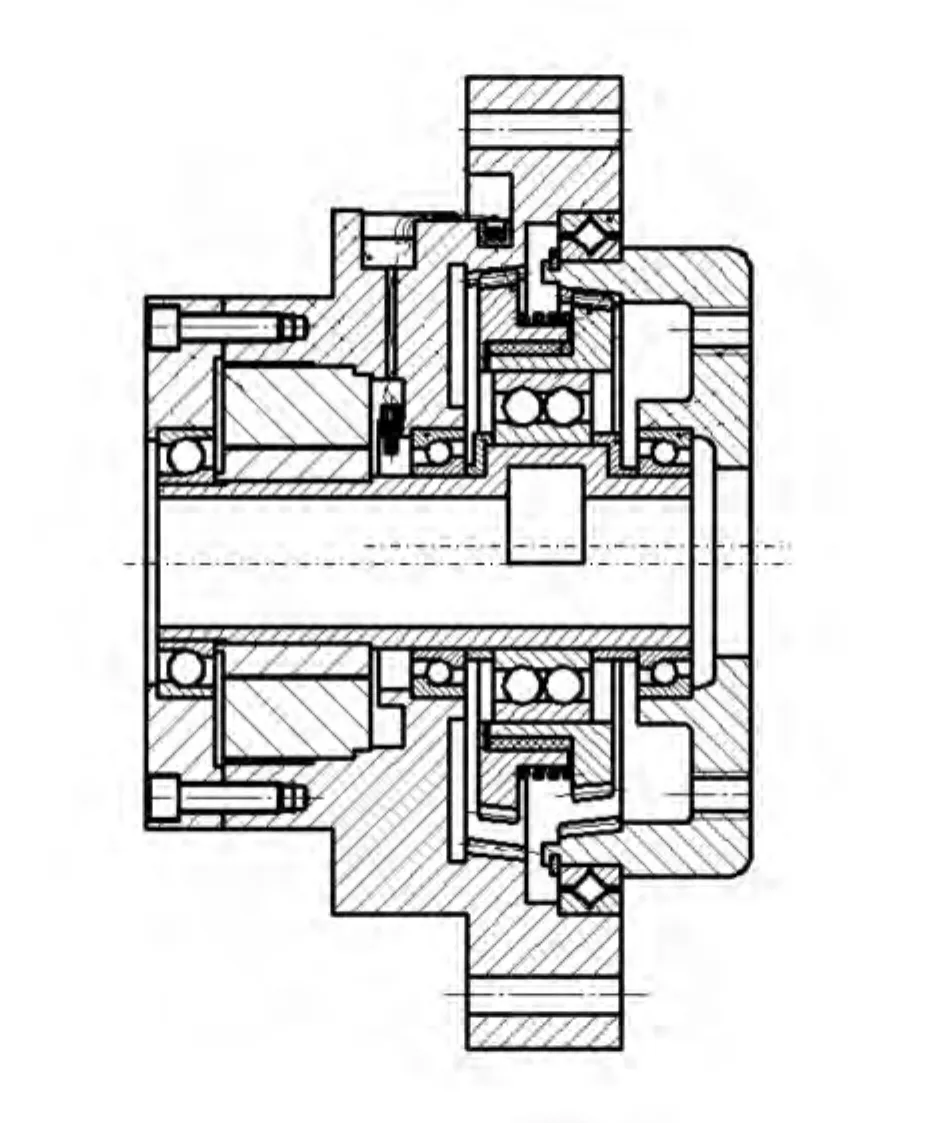
圖1 柔性濾波驅動機構Fig.1 The flexible filter driving mechanism

1.2 非線性摩擦特性

LuGre全面定義Stribeck特性、摩擦滯遲現象、stick-slip運動、靜摩擦力變化等各種摩擦特性。其模型表達式為

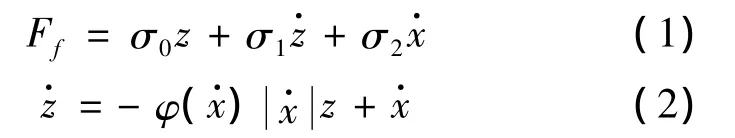
式中:σ0表示等效剛毛剛度，z表示剛毛變形量，σ1表示剛毛阻尼系數，σ2表示粘滯摩擦系數，表示接觸面相對速度，φ()表示速度函數:

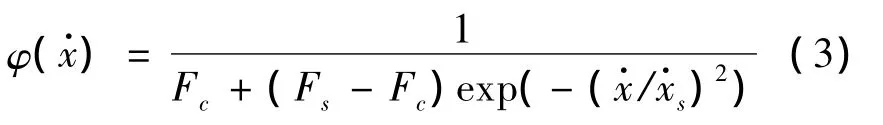
式中:Fc表示Coulomb摩擦力，Fs表示靜摩擦力，表示Stribeck速度。

1.3 動力學模型

對于柔性濾波驅動機構，考慮柔性變形、摩擦及傳動誤差等非線性因素的影響，建立二階非線性動力學模型如下

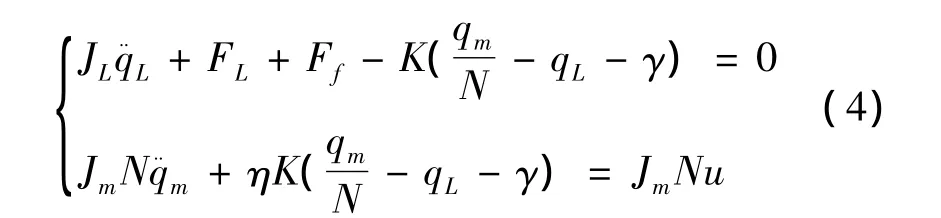
式中:Ff表示摩擦力矩，FL表示負載，K表示柔性剛度，JL、Jm表示驅動機構與電機轉動慣量，N表示減速器組件減速比，γ表示傳動誤差，u表示電機輸出力矩，η表示傳動系統效率，qL、和分別表示驅動機構位移、速度和加速度，qm、和分別表示電機位移、角速度、角加速度。

定義系統狀態變量x1=qL、x2、x3=qm、x4以及a=ηK/JmN和b=γ，則動態方程重寫如下

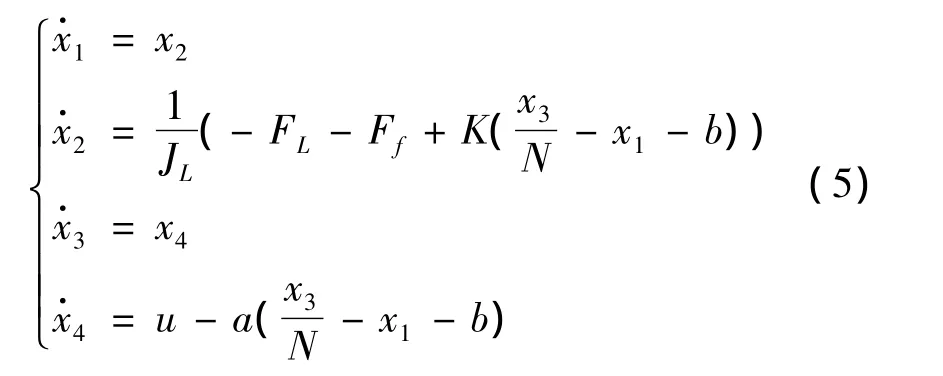
2 自適應動態面模糊控制器

2.1 模糊邏輯系統

模糊邏輯系統采用單點模糊化、乘積運算的模糊蘊涵關系、重心法解模糊和高斯函數的隸屬函數時，可以表示為

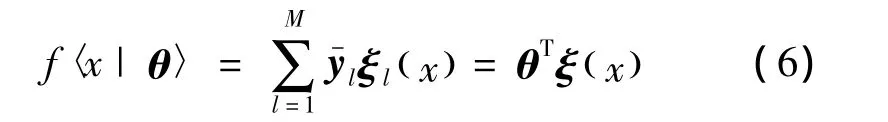
式中:f〈x|θ〉:Ωx?Rn→R表示模糊系統的輸出，表示未知參數向量，

選擇模糊基函數:

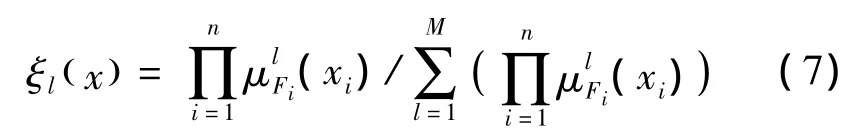
式中:μFi(xi)表示高斯型的隸屬函數。

對于緊集Ωy∈R中的連續非線性函數H(y)，存在模糊邏輯系統f和ε＞0，使得

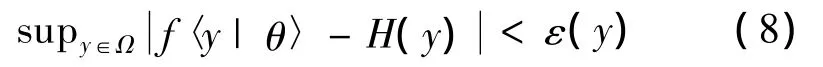
式中:ε(y)表示模糊逼近器的逼近誤差，并且滿足

2.2 控制器設計

控制器設計分為以下4個步驟:

1)定義面函數e1=x1-xd，則其導數為

取穩定化函數為

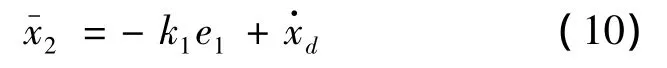
式中:k1為控制增益。為了消除對微分產生的大量導數項，引入另一個狀態變量x2f，并讓穩定化函數通過一階濾波器得到x2f，則

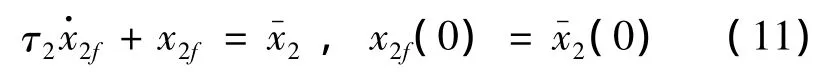
式中:τ2表示濾波器的時間常數。

2)定義面函數e2=x2-x2f，其動態方程為

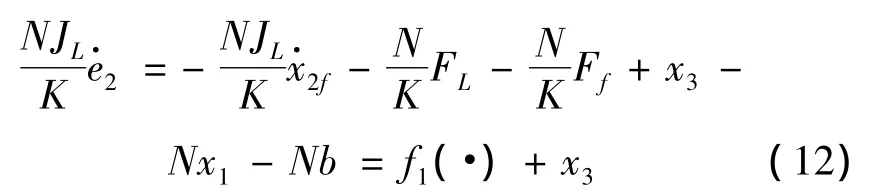
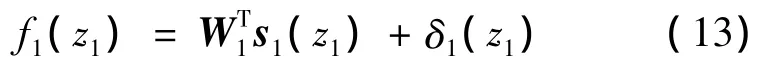
式中:δ1表示逼近誤差，并滿足不等式ε1＞0且任意小。

依據步驟1)的思想，取穩定化函數為

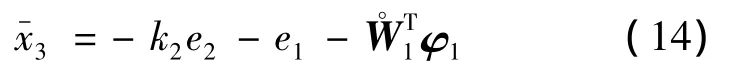
式中:k2表示控制增益，是W1的估計值。讓穩定化函數通過一階濾波器得到x3f，則

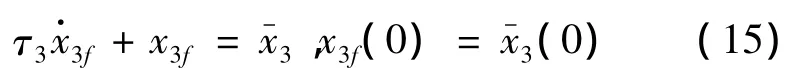
式中:τ3表示濾波器的時間常數。

3)定義面函數e3=x3-x3f，則它的導數為

根據步驟1)的思想，取穩定化函數為

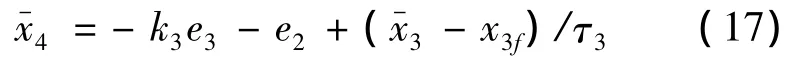
式中:k3表示控制增益。讓穩定化函數通過一階濾波器得到x4f，則

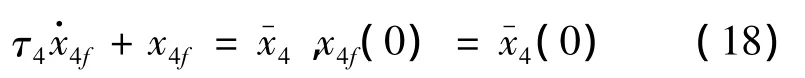
4)基于x4f定義面函數e4=x4-x4f，對其微分得

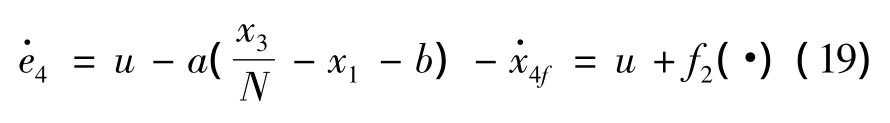
f2中既含有的導數，又含有未知量a、b和N，使得傳統方法設計控制器非常困難。利用模糊邏輯系統在一個緊集上以任意精度逼近任意連續函數的優點，即存在2(z)使得:

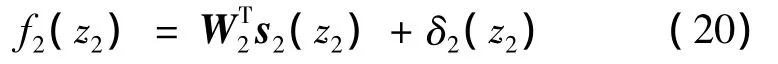
式中:δ2表示逼近誤差，并滿足不等式ε2＞0且任意小。

控制律設計為

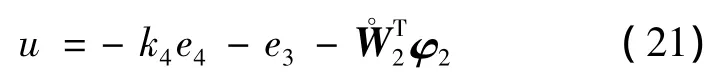
式中:k4表示控制增益，是W2的估計值。uf=G(s)u一階濾波器避開了代數循環問題，同時實際中執行器具有低頻特性，即uf≈u。

設計自適應律如下

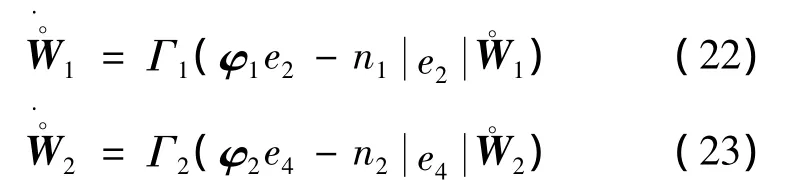
式中:n1、n2、Γ1和Γ2為正實數。

2.3 穩定性分析

濾波器誤差:

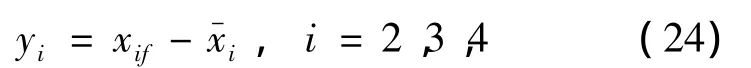
邊界層微分方程:

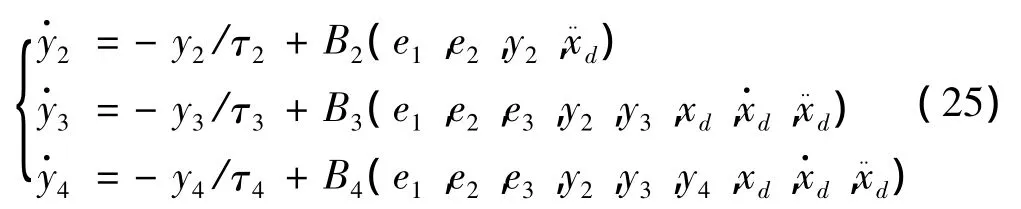
式中:

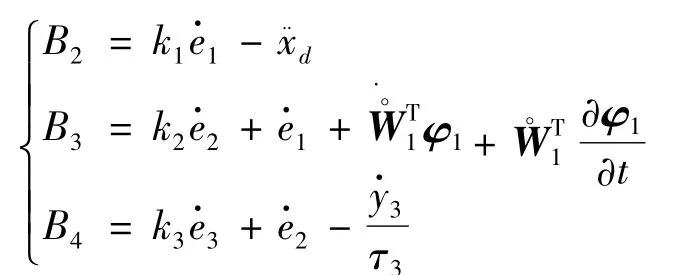
定義集合:

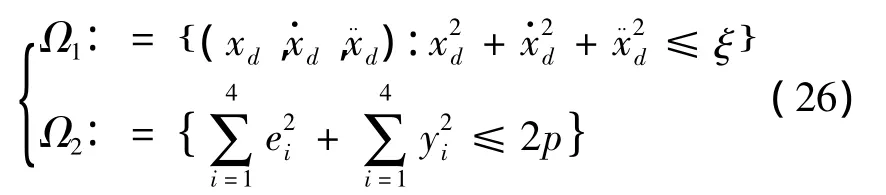
定理1 針對系統式(4)，給定一個正數p，對所有滿足初始條件V(0)≤p的情況，控制器式(21)和自適應律式(22)、(23)使得閉環系統信號半全局一致有界，跟蹤誤差收斂。

證明定義Lyapunov函數:

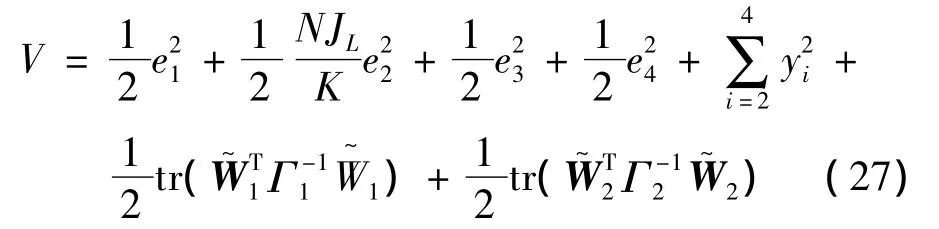
式中:tr(·)表示矩陣的跡。

對式(27)求導:

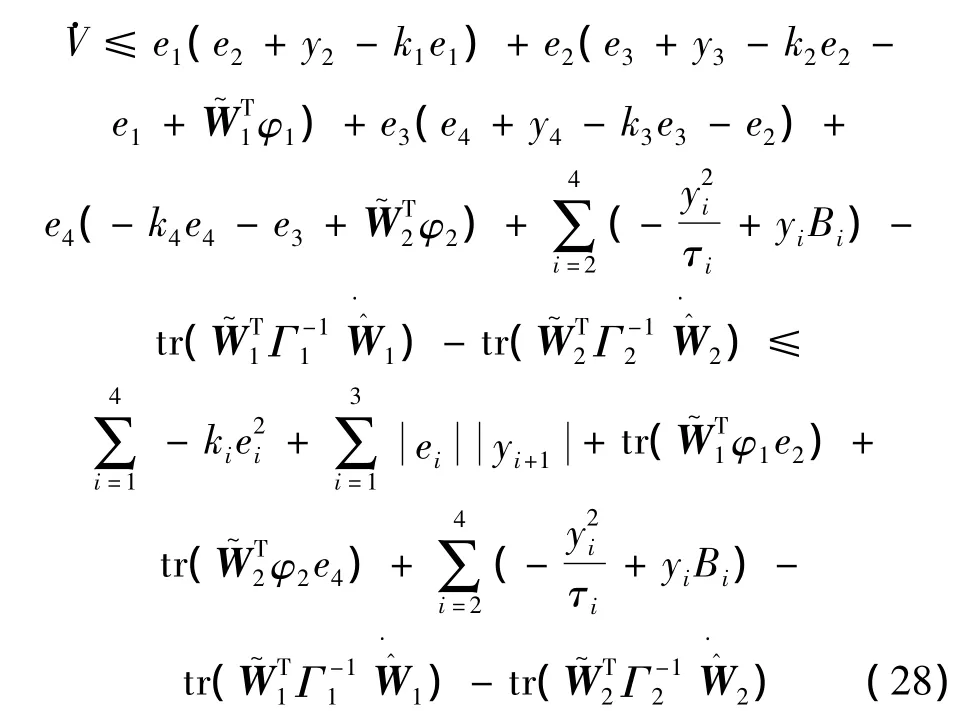
根據Young’s不等式，式(28)可得

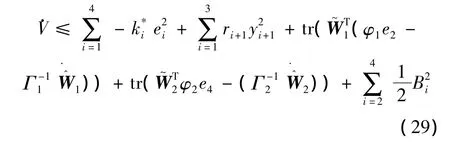
將自適應率代入可得

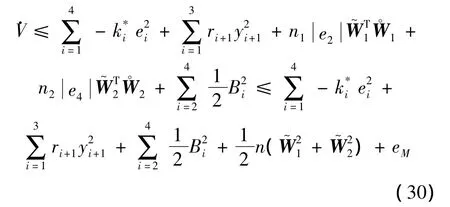
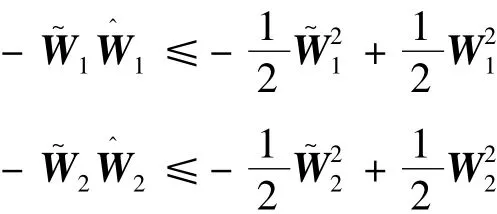
由式(30)可得

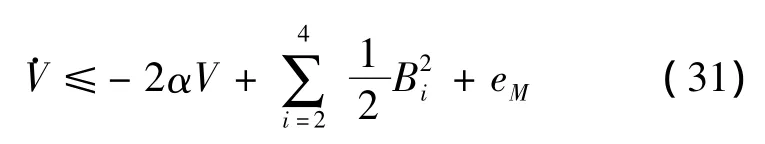
若，則≤0。如果V(0)≤p，?t≥0，系統誤差會在緊集內一致最終有界，且不大于

將式(31)求微分方程可得

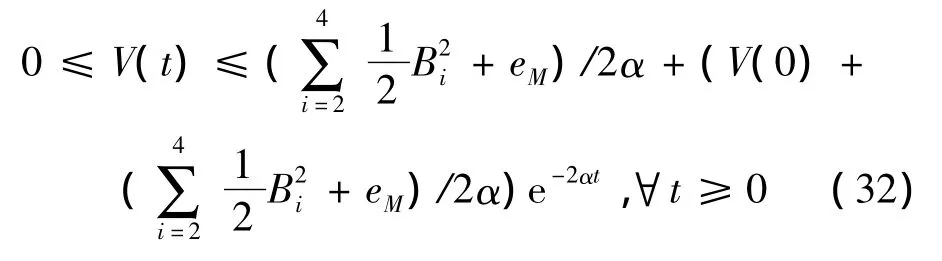
3 系統仿真實驗分析

本節將驗證柔性濾波驅動機構的自適應動態面模糊控制器的有效性和優越性。

選擇以下隸屬函數對系統輸入進行模糊化:

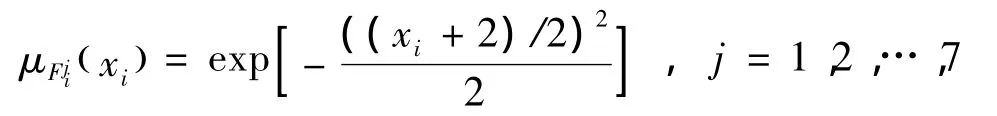
LuGre摩擦模型的參數值為

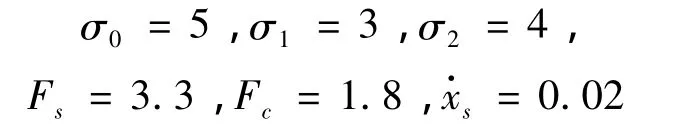
控制器參數為

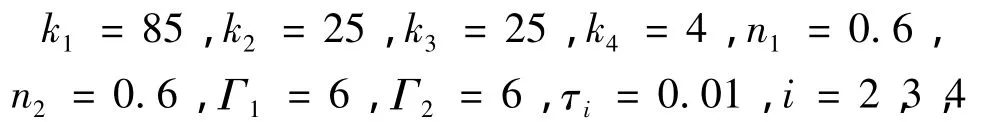
仿真實驗結果如圖2～5所示。圖2、3是系統對于正弦輸入的軌跡跟蹤效果，可以看出，由于摩擦等非線性項的作用，PID位置跟蹤存在“平頂”現象，速度跟蹤存在“死區”現象，控制魯棒性差，無法實現高精度控制。圖4中所提方案較PID實現高品質的軌跡跟蹤，其誤差迅速收斂在有界小區域內，體現了控制的有效性和優越性。

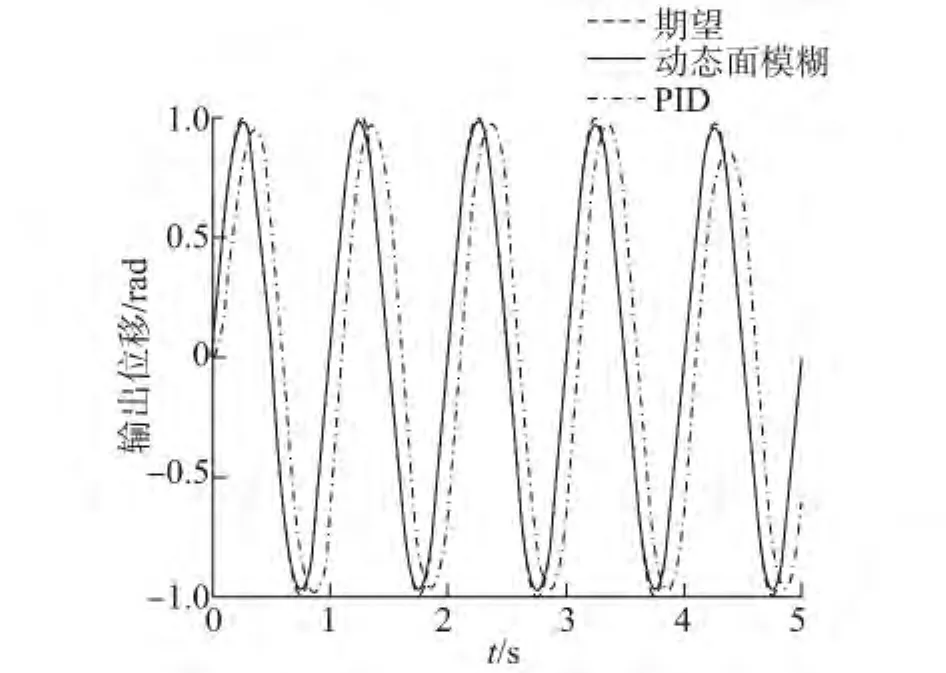
圖2 正弦位置跟蹤Fig.2 Sine position tracking

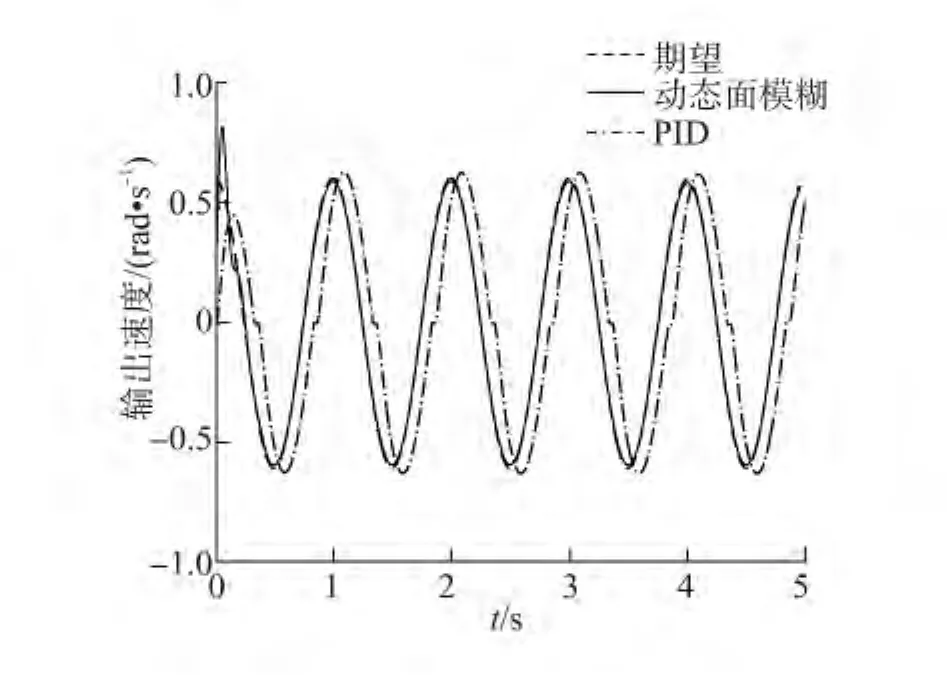
圖3 正弦速度跟蹤Fig.3 Sine velocity tracking

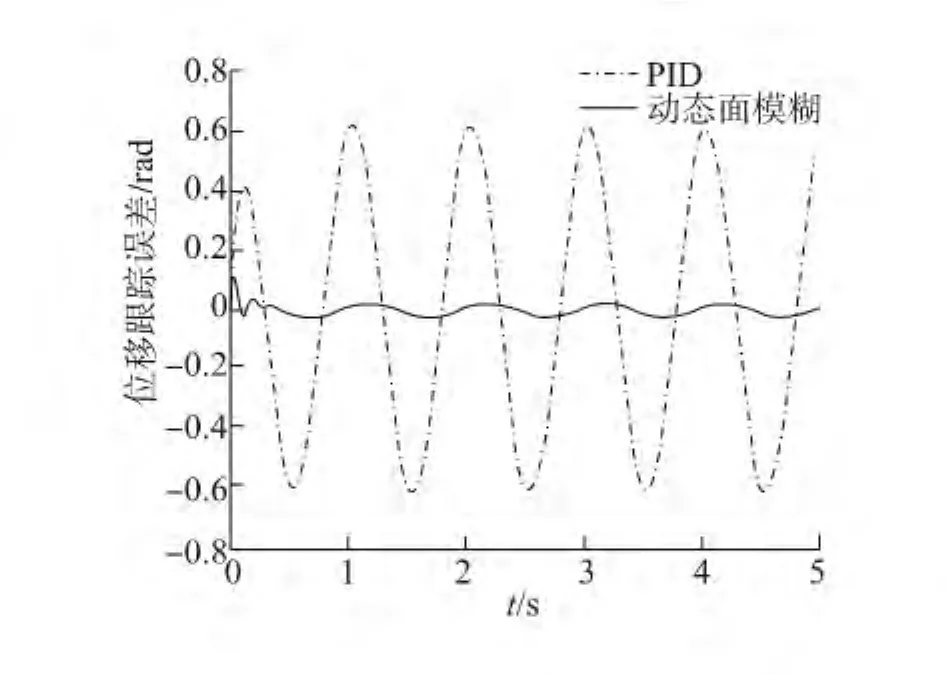
圖4 位移跟蹤誤差Fig.4 Position tracking error

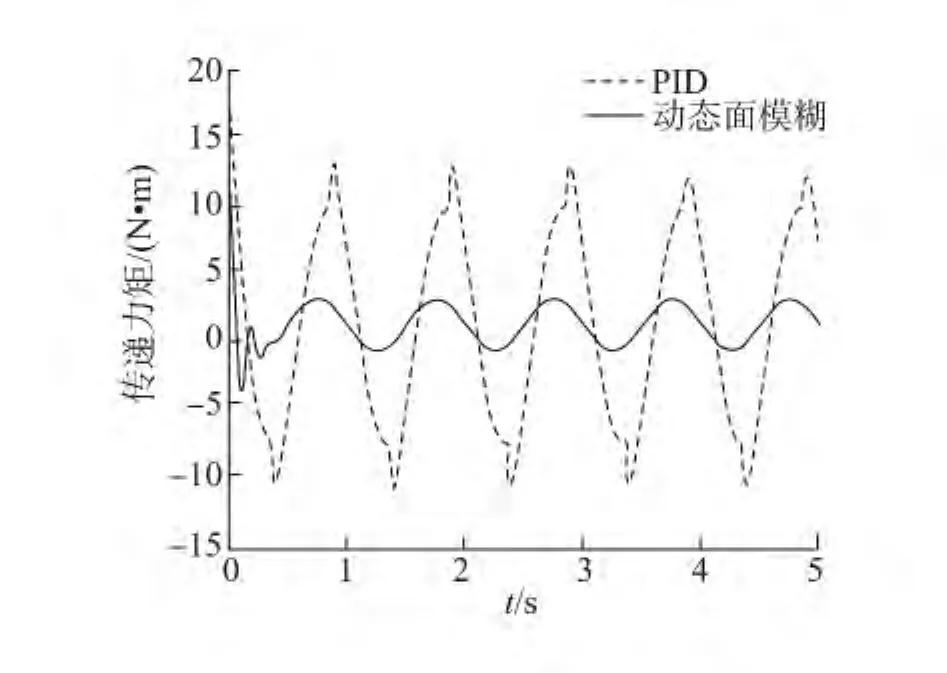
圖5 傳遞力矩Fig.5 Transmitted torque

從圖5狀態響應曲線可知，為加快系統的收斂速度，雖然控制輸入在初期需要的能量較大，但迅速趨于平衡狀態，抖動減小，所提方案較PID更能有效地抑制參數未知、擾動等，實現控制連續平穩。

4 結論

針對柔性濾波驅動機構的控制問題，本文利用模糊邏輯的萬能逼近特性，建立了柔性濾波驅動機構的自適應動態面模糊控制，并得出以下結論:

1)考慮非線性因素的影響，建立了合理的數學模型，所提控制器抑制了諸如摩擦等非線性項的影響，后續研究需要考慮體現溫度影響的摩擦模型和熱變形等影響因素。

2)將反步法控制的思想延伸到自適應動態面控制，克服相關文獻中“計算膨脹”的問題，同時利用Lyapunov理論證明了所提控制器的穩定性。

3)與傳統的PID對比，仿真實驗結果表明了所提控制器具有很好的跟蹤效果，使系統具有較強的魯棒性，從而使自適應動態面模糊控制技術具有一定地工程應用價值。

［1］王家序，李俊陽，周廣武，等.智能濾波驅動機構［P］.中國:ZL20111005460.7，2012-10-31.

［2］王家序，秦德成，張林川，等.濾波減速器輪齒表面瞬態微觀彈流潤滑模型［J］.四川大學學報:工程科學版，2013，45(1):202-207.WANG Jiaxu，QIN Decheng，ZHANG Linchuan，et al.Transient thermal micro-elastohydrodynamiclubrication model of filtering reducer［J］.Journal of Sichuan University:Engineering Science Edition，2013，45(1):202-207.

［3］王威，李瑰賢，宋玉玲.汽車轉彎高維非線性動力學特性研究［J］.哈爾濱工程大學學報，2009，30(6):676-685.WANG Wei，LI Guixian，SONG Yuling.High-dimensional nonlinear vehicular turning dynamics［J］.Journal of Harbin Engineering University，2009，30(6):676-685.

［4］DUAN H，LIU S，WANG D，et al.Design and realization of hybrid ACO-based PID and LuGre friction compensation controller for three degree-of-freedom high precision flight simulator［J］.Simulation Modeling Practice and Theory，2009，17(6):1160-1169.

［5］HAN S，LEE K.Robust friction state observer and recurrent fuzzy neural network design for dynamic friction compensation with backstepping control［J］.Mechatronics，2010，20(3):381-401.

［6］WANG Y，WANG D，CHAI T.Modeling and control compensation of nonlinear friction using adaptive fuzzy systems［J］.Mechanical Systems and Signal Processing，2009，23(6):2445-2457.

［7］LIN J，CHEN C.Positioning and tracking of a linear motion stage with friction compensation by fuzzy logic approach［J］.ISA Transactions，2007，46(3):327-342.

［8］SEYFFERTH W，MAGHZAL A，ANGELES J.Nonlinear modeling and parameter identification of harmonic drive robotic transmissions［C］//Proceedings-IEEE International Conference on Robotics and Automation.Nagoya，1995:3027-3032.

［9］CHIEN M，HUANG A.Adaptive control for flexible-joint electrically driven robot with time-varying uncertainties［J］.IEEE Transactions on Industrial Electronics，2007，54(2):1032-1038.

［10］LI Y，TONG S，LI T.Adaptive fuzzy output feedback control for a single-link flexible robot manipulator driven DC motor via backstepping［J］.Nonlinear Analysis:Real World Applications，2013，14(1):483-494.

［11］劉金琨.機器人控制系統的設計與Matlab仿真［M］.北京:清華大學岀版社，2008:345-401.LIU Jinkun.Robotics control system design and simulation via Matlab［M］.Beijing:Tsinghua University Press，2008:345-401.

［12］NA J，REN X，HERRMANN G，et al.Adaptive neural dynamic surface control for servo systems with unknown deadzone［J］.Control Engineering Practice，2011，19(11):1328-1343.

［13］HAN S，LEE J.Adaptive dynamic surface control with sliding mode control and RWNN for robust positioning of a linear motion stage［J］.Mechatronics，2012，22(2):222-238.

［14］WANG D，HUANG J.Neural network-based adaptive dynamic surface control for a class of uncertain nonlinear systems in strict-feedback form ［J］.IEEE Transactions on Neural Networks，2005，16(1):195-202.