欠驅動水面船舶非線性信息融合航跡跟蹤控制
胡洲,王志勝,甄子洋
(南京航空航天大學自動化學院,江蘇南京210016)
欠驅動系統是指控制輸入向量空間的維數小于其廣義坐標向量空間維數的系統[1]。近年來,有關欠驅動系統控制問題的挑戰性引起了控制學界的關注。常規船舶是一類典型的欠驅動系統,它依靠發動機轉速產生的推力和方向舵偏轉產生的轉彎力矩來實現水面上2個坐標位置和航向的控制。由于欠驅動水面船舶在橫向上未裝備驅動裝置,且其動力學方程帶有非完整約束條件,不滿足著名的Brockett定理的必要條件[2],所以要實現欠驅動船舶的航跡跟蹤控制較為困難[3]。目前,該問題已成為控制領域內的一個研究熱點。文獻[4-5]對欠驅動船舶的直線航跡跟蹤控制的穩定性進行了研究。文獻[6]利用反步技術和輸出重定義提出了一種全局指數穩定的直線航跡控制方法。文獻[7]基于反步法和Lyapunov直接法設計了曲線航跡跟蹤控制律。文獻[8]提出了一種新型的非線性滑模控制律設計方法,實現了船舶跟蹤虛擬船產生的參考軌跡。文獻[9]采用了一種魯棒自適應控制策略解決了帶不確定動態的船舶路徑跟蹤控制問題。
以上方法都不同程度的存在著局限性,或者比較簡單,只考慮了直線航跡跟蹤控制問題[4-6,10],或者過于復雜[7-9],難于實現。本文采用了一種非線性信息融合控制方法[11]用于解決欠驅動水面船舶的曲線航跡跟蹤控制問題,該方法基于被控對象的離散狀態模型實現,具有良好的工程應用前景。
1 欠驅動水面船舶控制系統建模
圖1為一個欠驅動水面船舶的運動示意圖。對于多數船舶的控制問題,通常只考慮船舶在水平面內的運動,即只關注縱蕩、橫蕩和艏搖運動,而忽略垂蕩、縱搖及橫搖運動,本文旨在為欠驅動水面船舶的航跡跟蹤控制問題找到一種新的解決方法,為了避免船舶的數學模型過于復雜,船舶水平面運動方程和動力學方程均基于如下假設條件:
1)船體坐標系的軸位于船的慣性主軸上;
2)原點在船體重心上;
3)船體質量均勻分布;
4)船關于2個坐標軸對稱;
5)不考慮水流速度。
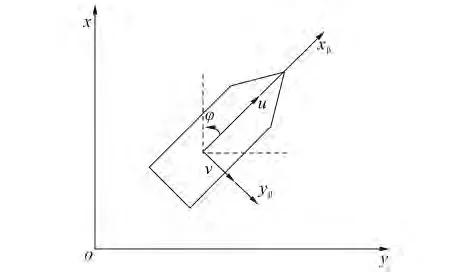
圖1 欠驅動水面船舶運動示意圖Fig.1 Themotion diagram of underactuated vessel
根據文獻[7-8,12],欠驅動水面船舶的運動學方程和動力學方程可以表示為
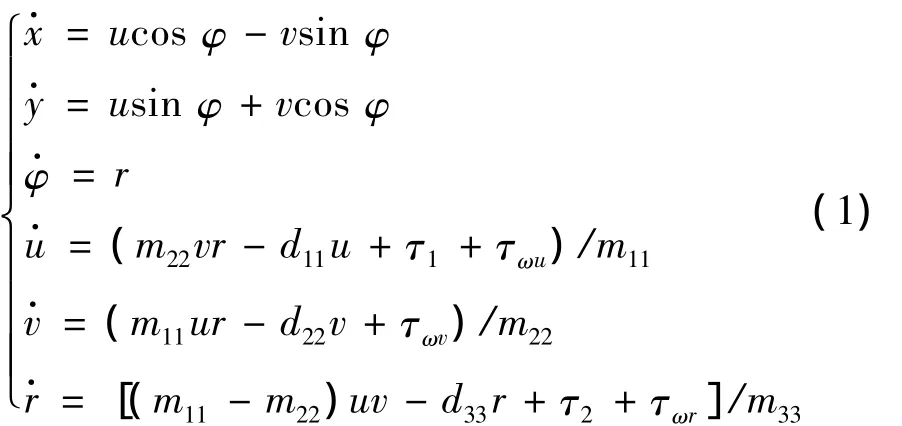
式中:m11、m22、m33為慣性參數,d11、d22、d33為水動力阻力參數,x、y為船舶在水平面參考坐標系中的位置參數,φ為航向參數,u、v分別為船舶沿本體坐標系xβ軸和yβ軸方向上的線速度,r為船舶的航向角速度,τ1、τ2分別為縱向推進力和轉向力矩,τωu、τωv和 τωr為風、浪和流等環境因素引起的外界干擾,且滿足有界條件 τωu≤ τωu(max)< ∞,τωv≤ τωv(max)< ∞, τωr≤ τωr(max)< ∞。
令x1=x,x2=y,x3= φ,x4=u,x5=v,x6==r,u1=τ1,u2=τ2。則式(1)變為

定義狀態向量x=[x1x2x3x4x5x6],控制向量u=[u1u2],可將船舶控制模型簡化為
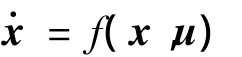
非線性信息融合控制算法需要基于被控對象的離散化數學模型實現,本文采用泰勒級數法[13]:
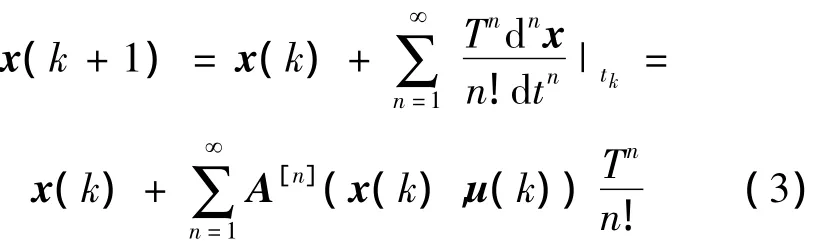
將式(2)離散化。式中:A[n](x,u)可由如下的遞歸表達式依次求出:
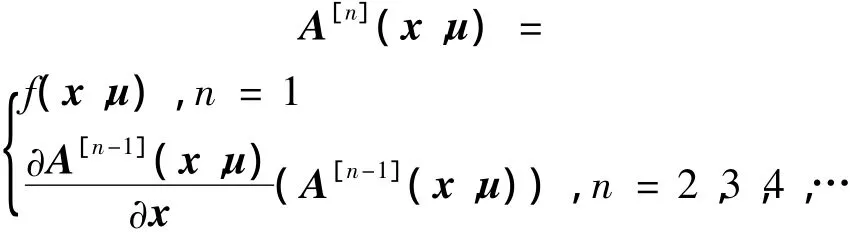
離散化后的模型可表示為如式(3)所示的級數形式。如果采樣時間T取值較大,則需要保留二階項或更高階項以獲得較為精確的模型。一般來說,如果T≤0.1 s,則式(3)中的一階項為主要部分,二階及二階以上的項可忽略。在本文中,取T=0.02 s,對式(3)保留一階項,可得船舶系統的非線性離散狀態方程如下

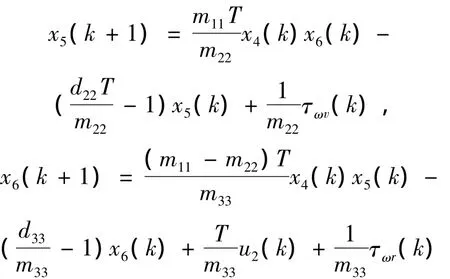
大多數船舶的控制問題通常只考慮船舶在水平面內的運動,可構造輸出方程如下

2 非線性信息融合控制方法
2.1 控制問題描述
考慮非線性離散控制系統[11]:
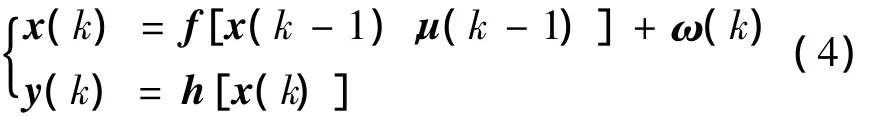
式中:x(k)∈Rn為狀態量,u(k)∈Rm為控制量,ω(k)為干擾輸入,y(k)∈Rp為輸出量,f(·,·)為Rn×Rm上的n維光滑向量場,h(·)是Rp上的p維光滑單調向量場。x(0)=x0。對于信息融合最優跟蹤控制問題,可以建立控制性能指標:
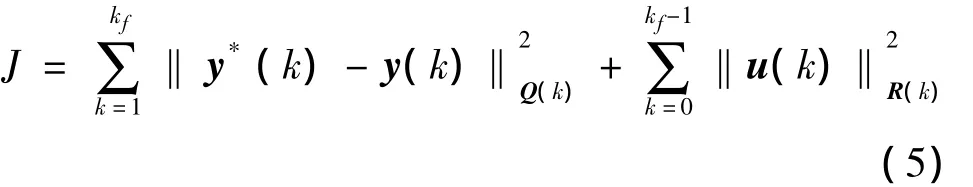
即求出一組控制序列u(k),使該式達到極小值。式中:y*(k)為期望軌跡,上式第一項表示在控制過程中,要求各維實際輸出都必須跟蹤期望輸出,跟蹤誤差要最小,Q(k)陣表示對各維輸出跟蹤誤差的約束要求,可以看作是關于跟蹤誤差的信息量;第二項表示在整個控制過程中,對各維控制量的能量要求,在輸出量滿足指標要求的前提下,控制能量要最小,R(k)陣表示對各維控制量的能量約束要求,可以看作是關于控制能量的信息量,R(k)和Q(k)陣均為正定對稱陣。
2.2 非線性信息融合控制算法設計
若將性能指標函數式(5)表示為統一的信息模式,則有y*(k)=h[x(k)]+m(k),m(k)為均值為零,方差為Q-1(k)的白噪聲;0=u(k)+n(k),n(k)為均值為零,方差為R-1(k)的白噪聲。
從信息融合的角度,上述控制問題共包含3部分信息:1)由式(4)所決定的等式約束信息;2)期望跟蹤軌跡y*(k)的跟蹤信息;3)希望每個u(k)都盡可能小的控制約束信息。信息融合控制的任務,就是融合這些信息,求出(k)。
定理1[11]若關于x的各種信息表示為
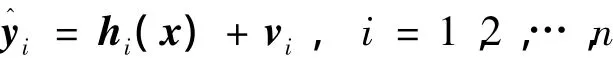
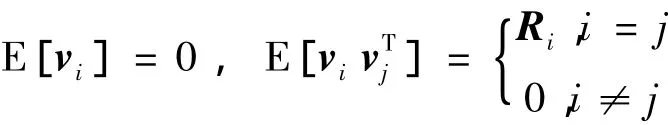
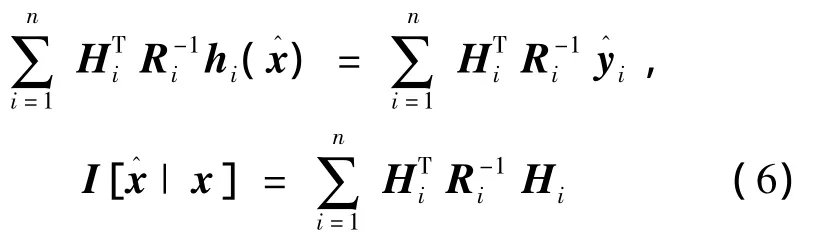
式中:Hi= ?hi/?x|x=x^,I[|x]表示關于 x 的信息量。定理1為非線性信息融合估計定理,式(6)為信息融合估計的統一非線性模型。稱為信息關于自身的信息量,記作I[|yi]=;Hi為關于被估計量x的信息量,記作I[|x]=Hi。所有關于被估計量x的信息的信息量之和等于最優融合估計關于自身的信息量,即 I[|x] =。通常,信息量與該信息的協方差互為倒數。
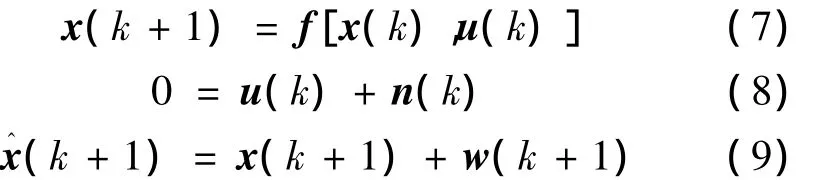
式中:w(k+1)為均值為零,方差為P-1(k+1)的白噪聲。將式(7)代入式(9),運用定理1融合關于u(k)的信息,可得
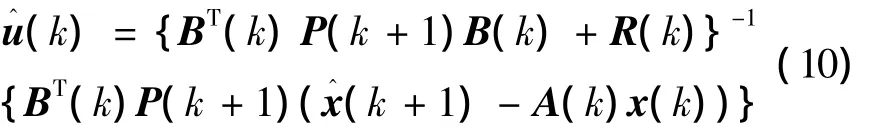
式中:
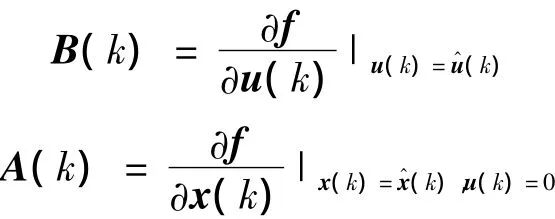
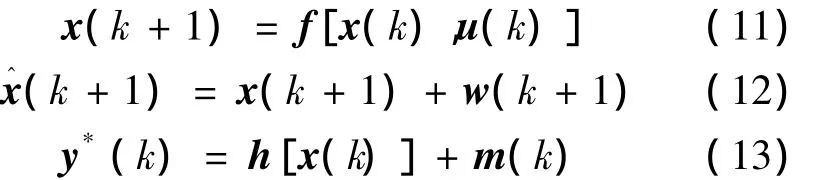
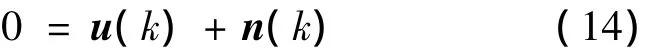
將式(12)、(14)代入式(11),可得
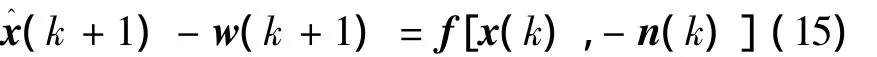
式(15)可變換為
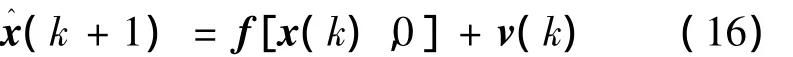
式中:v(k)為均值為零,方差為M-1(k)的白噪聲。
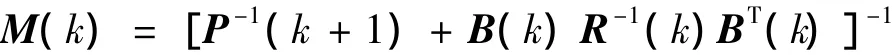
運用定理1,融合式(13)、(16)中關于x(k)的信息,可得
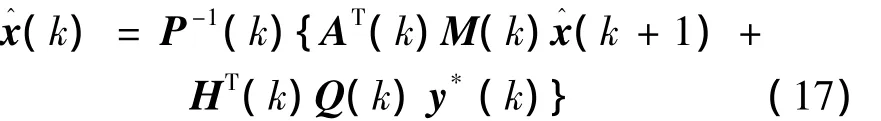
式中:
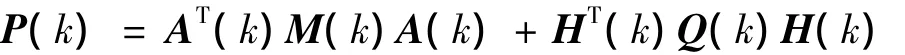
2.3 非線性信息融合控制算法流程
1)置控制向量初值u^(0)(0)=0,狀態向量初值 x(0)(0)=x0,求 x(0)(k+1)=f[x(0)(k),u^(0)(k)],k=0~(kf-1),kf為預見步數。
2)置迭代序號i=1。
3)求下列偏導數:
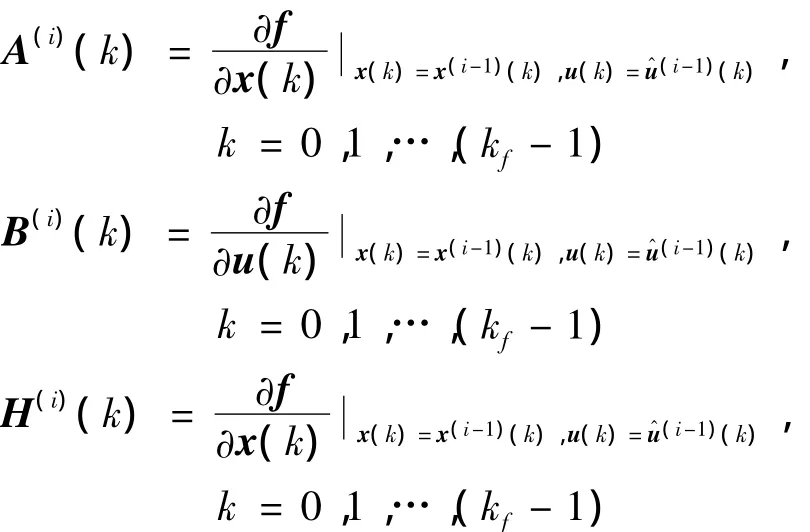
4)置:
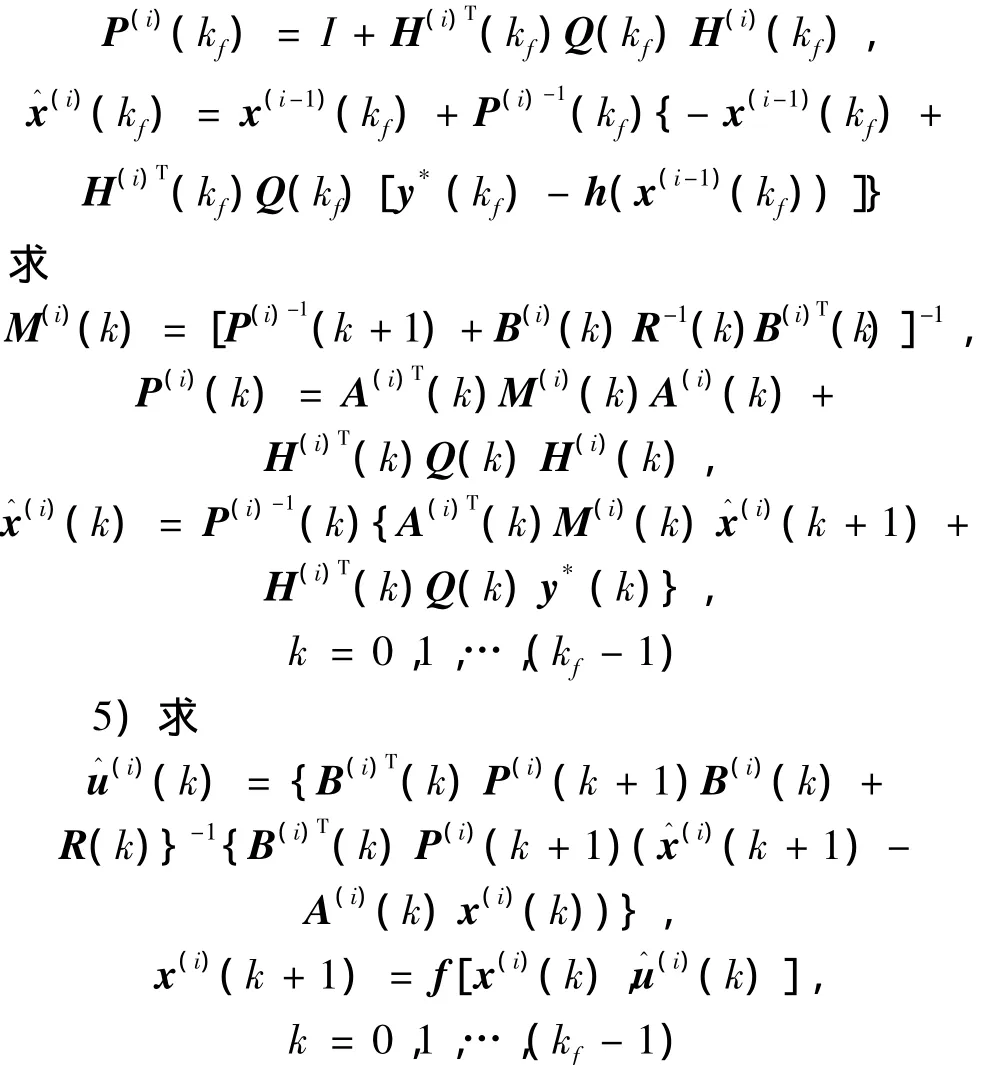
從上面的算法流程中可以看出,控制律的求解過程中沒有求解非線性黎卡提方程,這為該算法的工程實現帶來了很大的方便。
3 船舶的信息融合控制仿真研究
本文所取的船舶實驗模型參數與文獻[7]相同,m11=200 kg,m22=250 kg,m33=80 kg,d11=70 kg/s ,d22=100 kg/s,d33=50 kg/s。
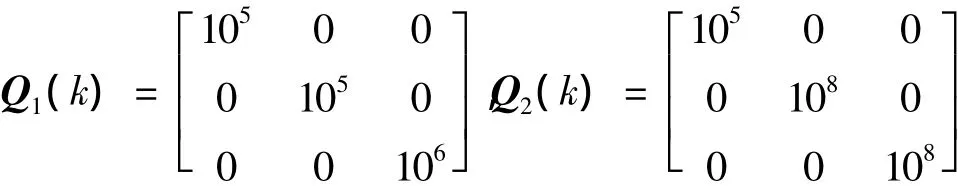
采樣周期取T=0.02 s,預見步數取kf=50步.環境干擾 τωu(t)= τωv(t)= τωr(t)=5+10sin t,下面分以下4種情況進行討論。
情況1:期望跟蹤航跡和航向分別為圖2、3所示,初始狀態x(0)=[0 0 0 0 0 0],Q(k)=Q1(k),無環境干擾。
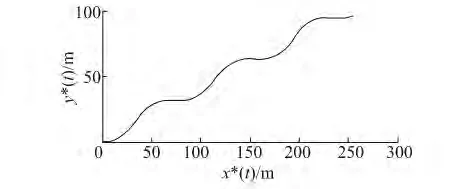
圖2 期望跟蹤航跡Fig.2 The expectation tracking trajectory
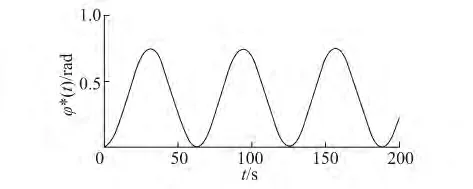
圖3 期望跟蹤航向Fig.3 The expectation tracking course
情況2:期望跟蹤航跡、航向和初始狀態保持不變,Q(k)=Q2(k),無環境干擾。
情況3:期望跟蹤航跡、航向和初始狀態保持不變,Q(k)=Q1(k),有環境干擾。
情況4:期望跟蹤航跡為x*(t)=5cos t,y*(t)=5sin t,期望跟蹤航向φ*(t)=t+π/2,初始狀態保持不變,Q(k)=Q1(k),無環境干擾。
為了驗證非線性信息融合控制算法對欠驅動水面船舶路航跡跟蹤的控制效果,首先需要設計一條期望的航跡,可以通過運動規劃解決。對于全驅動系統,運動規劃總是認為系統在其位形空間內的所有運動都是允許的,然而對于欠驅動系統,因為系統受到非完整約束,并不是所有狀態空間都是可達的,航跡的生成空間受到很大的限制。本文的主要目的不是討論航跡規劃問題,針對情況1~3,簡單的采用開環的方法生成一條航跡,針對情況4,采用了與文獻[7]相同的航跡參數。
設 ex(t)、ey(t)、eφ(t)為跟蹤誤差。由圖4可以看出,在信息融合控制器的作用下,船舶的曲線航跡跟蹤誤差始終保持在一個較小的范圍內,這說明了該算法對欠驅動水面船舶的航跡跟蹤控制具有良好的效果。圖4、5為信息權陣 Q(k)分別取Q1(k)和Q2(k)時的航跡跟蹤誤差曲線,可以看出,通過調節信息權陣Q(k)的取值,可以得到不同的跟蹤控制效果。一般而言,增大Q(k)中的某一對角元素的值,可以改善相對應的輸出量的控制效果,但其他輸出量的控制效果可能會變差。如圖5所示,Q2(k)中增大了橫向和航向的跟蹤誤差信息量,所以這2個輸出的跟蹤誤差變小,但縱向輸出的跟蹤誤差卻變得比原來大。所以Q(k)陣的取值應折衷選取。
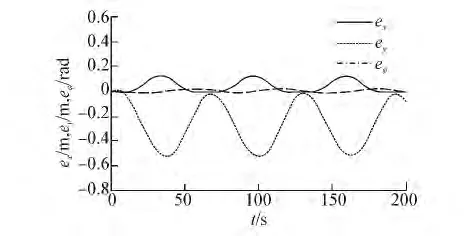
圖4 情況1時的航跡跟蹤誤差Fig.4 The tacking error of case 1
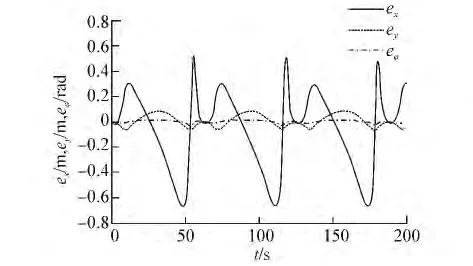
圖5 情況2時的航跡跟蹤誤差Fig.5 The tacking error of case 2
圖6為增加環境干擾后的跟蹤效果,干擾分為常值擾動和正弦擾動,從圖6中可以看出橫向誤差曲線存在一定的常值偏差,所以信息融合控制算法對橫向常值擾動的抗干擾能力較弱,所有通道對正弦擾動均有良好的抗干擾能力,誤差曲線都保持在一個較小的范圍內沒有發散,表明了信息融合控制器對環境干擾具有一定的魯棒性能。
圖7為情況4時的航跡跟蹤誤差,該情況與文獻[7]所采用的模型參數和航跡參數相同,文獻[7]基于反步法和Lyapunov直接法設計了曲線航跡跟蹤控制律,綜合比較可得:圖7中跟蹤誤差曲線的收斂速度與文獻[7]基本相當,跟蹤效果比較理想。
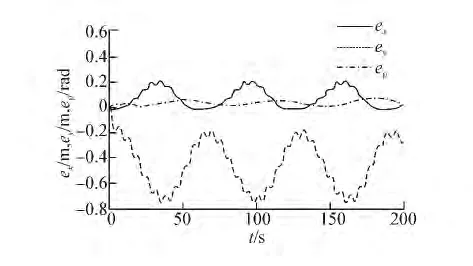
圖6 情況3時的航跡跟蹤誤差Fig.6 The tacking error of case 3
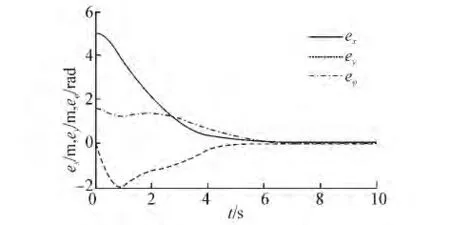
圖7 情況4時的航跡跟蹤誤差Fig.7 The tacking error of case 4
4 結論
本文得出以下幾點結論:
1)采用非線性信息融合控制算法設計欠驅動水面船舶的航跡最優跟蹤控制律,可以實現對船舶位置和航向良好的同步跟蹤控制,同時避免了求解非線性黎卡提方程。
2)在控制器設計過程中,信息權陣Q(k)應折衷選取,以使各輸出通道具有均衡的控制效果。
3)仿真實驗表明信息融合控制算法對環境干擾具有一定的魯棒性能,但對橫向常值擾動的抗干擾能力較弱。
[1]SPONG M.Partial feedback linearization of underactuated mechanical systems[C]//Proceedings of the IEEE/RSJ/GI International Conference on Intelligent Robots and Systems.Munich,Germany,1994:314-321.
[2]BROCKETTRW.Asymptotic stability and feedback stabilization[J].Differential Geometric Control Theory,1983:181-191.
[3]JIANG Z P.Global tracking control of underactuated ships by Lyapunov's direct method[J].Automatica,2003,38(2):301-309.
[4]周崗,姚瓊薈,陳永冰,等.不完全驅動船舶直線航跡控制穩定性研究[J].自動化學報,2007,33(4):378-383.ZHOU Gang,YAO Qionghui,CHEN Yongbing,et al.A study of stability of straight-line tracking control system for underactuated ship[J].Acta Automatica Sinica,2006,33(4):378-383.
[5]周崗,姚瓊薈,陳永冰,等.一類船舶直線航跡控制系統全局漸近穩定的充分條件及推論[J].自動化學報,2007,33(11):1204-1207.ZHOU Gang,YAOQionghui,CHEN Yongbing,et al.Suffient conditions of global asymptotic stability and deductions for ship 's straight-line tracking control systems[J].Acta Automatica Sinica,2007,33(11):1204-1207.
[6]JIANG Z P.Robust global stabilization of underactuated ships on a linear course:state and out-put feedback[J].International Journal of Control,2003,76(1):1-17.
[7]曾薄文,朱齊丹,于瑞亭.欠驅動水面船舶的曲線航跡跟蹤控制[J].哈爾濱工程大學學報,2011,32(10):1317-1322.ZENG Bowen,ZHU Qidan,YU Ruiting.Curve tracking control of an underactuated surface vessel[J].Journal of Harbin Engineering University,2011,32(10):1317-1322.
[8]孟威,郭晨,孫富春.欠驅動水面船舶的非線性滑模軌跡跟蹤控制[J].哈爾濱工程大學學報,2012,33(5):585-589.MENGWei,GUO Chen,SUN Fuchun.Nonlinear sliding mode tracking control of underatuated surface vessels[J].Journal of Harbin Engineering University,2012,33(5):585-589.
[9]MENGWei,GUO Chen,LIU Yang.Robust adaptive path following for underactuated surface vessels with uncertain dynamics[J].Journal of Marine Science and Application,2012,11(2):244-250.
[10]廖煜雷,萬磊.欠驅動船舶直線航跡的滑模控制方法[J].應用科技,2011,38(11):13-17.LIAO Yulei,WAN Lei.Sliding-mode straight-line tracking control for underactuated vessels[J].Applied Science and Technology,2011,38(11):13-17.
[11]WANG ZS,WANG D B,ZHEN ZY.Primary exploration of nonlinear information fusion control theory[J].Science in China Series F:Information Sciences,2007,50(5):686-696.
[12]FOSSEN T I.Guidance and control of ocean vehicles[M].Upper Saddle River, New York:Wiley Interscience,1994:7-56.
[13]ZHANG Z,AN D U,KIM H,et al.Comparative study of matrix exponential and Taylor series discretization methods for nonlinear ODEs[J].Simulation Modeling Practice and Theory,2009,17(5):471-484.

