基于ANSYS二次開發的風力機葉片結構優化

陳進，馬金成，汪泉，郭小鋒，李松林

(重慶大學機械傳動國家重點實驗室，重慶400030)

風輪葉片是風力發電裝置最關鍵、最核心的部分之一，為提高其發電性能和功率，葉片翼型被設計得往往異常復雜［1］，并且隨著風力機單機容量增大，葉片長度也相應增加。為保證其足夠的強度和疲勞壽命，水平軸風力機葉片基本由復合材料制造而成，其成本占整個裝置成本的15% ～20%，因此葉片的設計和選材非常重要［2］。復合材料葉片結構設計及優化一直是國內外學者所探究的熱點，C.Kong等針對變載荷和疲勞載荷對風力機葉片結構的影響做出了深入研究，并結合實驗對比論證其分析的準確性［3］，Erik Lund等采用離散化方法對簡化的風力機葉片殼單元進行了結構鋪層優化，驗證了該方法的優越性［4］，C.C.Liao等采用 FAST 軟件與改進的粒子群算法對風力機葉片截面鋪層進行了優化，并利用FOCUS5軟件對優化結果進行評估，從而驗證該方法的有效性［5］。而解決葉片強度、剛度與重量之間的矛盾［6］對風力機葉片設計者來說也是一個不小的挑戰。本文針對某850 kW風力機葉片，為降低材料成本，同時將使用風場由一類風區拓展至二類風區，在保證葉片外形的基礎上，將其原有環氧玻纖改為聚酯玻纖，并重新進行鋪層設計［7］，并結合優化算法，以質量最小為目標，對葉片的鋪層及結構進行優化。通過該研究降低了葉片質量，并為葉片氣動、結構一體化設計提供了可能。

1 鋪層策略

1.1 材料分析

針對此850 kW葉片，其設計總長為28 m，選用聚酯玻纖作為葉片鋪層材料，設計時采用單向布EKU1250、雙向布 EKB800和三向布 EKT800這3種，其具體鋪設方式見圖1。

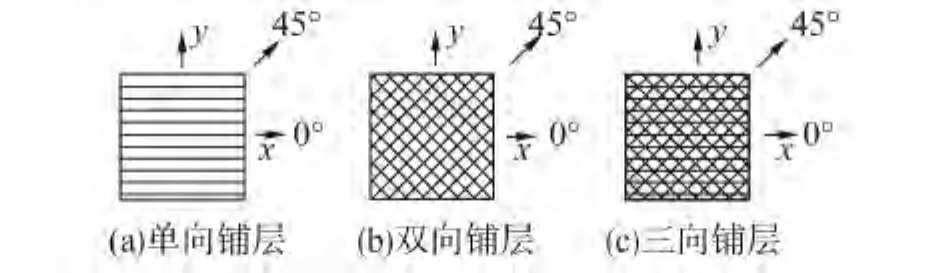
圖1 玻纖布鋪層類型Fig.1 Kinds of layout about fiberglass

泡沫夾心材料采用PVC，翼面上的泡沫材料由于被分割為小塊，有樹脂灌入，材料特性呈橫觀各向同性，以泡沫1表示;而腹板中泡沫沒有被分割，仍為各向同性，以泡沫2表示。此外葉片外層還有一層膠衣布。各種材料力學性能見表1。表1中:Vf為材料玻纖含量百分比，Ex為x方向的彈性模量，Ey為y方向的彈性模量，νxy為主泊松比，Gxy為x-y平面的剪切模量。

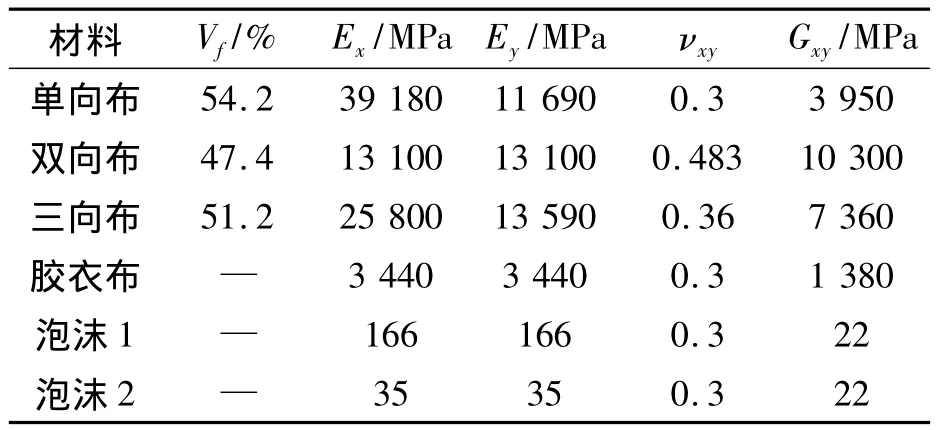
表1 葉片材料力學性能Table 1 Mechanical properties of the blade material

1.2 鋪層設計

典型葉片截面結構如圖2，其采用翼面、主梁、雙腹板和前、后緣增強的基本結構形式。

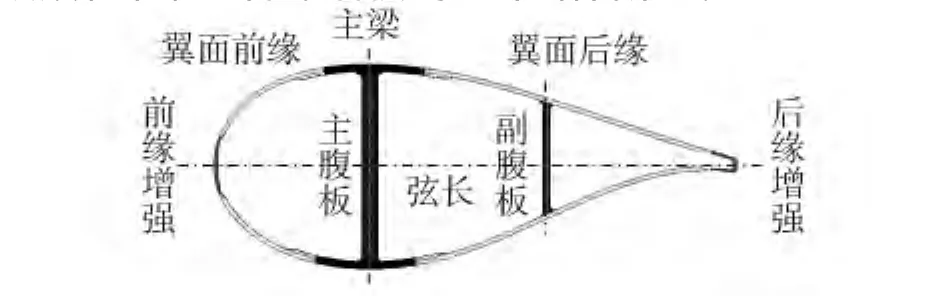
圖2 葉片截面結構Fig.2 Structure of blade section

根據葉片實際結構并參考相關資料［8］，得到葉片各處具體鋪層方式及效果:

1)翼面用來保持葉片氣動外形，采用夾芯結構，其由外層雙向布，中間泡沫1組成，其主要作用是增加翼面厚度，提高其抗彎剛度。

2)主梁搭在主腹板兩端，其為主要的承載結構，由外層雙向布和中間可達49層的單向布構成，其主要承受揮舞方向的載荷。

3)腹板為“三明治”夾芯結構，由外層雙向布和中間泡沫2組成，其承擔葉片彎曲產生的剪切力，并將其傳遞到主梁，轉化為主梁的拉伸和壓縮。

4)葉片前、后緣處曲率變化很大，容易產生應力過大的情況，為保證其強度，需在此處鋪設加強層，由外層雙向布和內層單向布構成。

5)整個葉片的載荷都需通過主梁傳遞至葉根，因此葉根承受很大的載荷，需要增設更多的鋪層，其由外層雙向布，中間單向布、雙向布交替，內層三向布構成，其最厚處可達99層。

2 基于ANSYS二次開發的參數化建模

風力機葉片有限元建模的傳統方式是通過變化后的翼型空間坐標，采用成熟的三維造型軟件如:P/ROE、UG、Solidworks等繪出葉片面結構［9］，然后再導入ANSYS、ABAQUS等有限元軟件中進行分析。這樣做的優點是采用成熟的造型軟件建模相對簡單，曲面過渡平滑，缺點是導入有限元軟件后修復過程繁瑣且參數改變后需重新建模，不利于結構優化。本文提出MATLAB與ANSYS相結合的方法，在ANSYS中由底至頂建立其參數化幾何模型。具體思路如下:編寫MATLAB程序生成葉片空間三維坐標，并以特定的格式輸出保存［10］;運用APDL語言編寫宏文件與MATLAB進行數據交換，導入ANSYS中生成幾何坐標點;利用ANSYS的BSPLIN功能將離散的空間坐標連接形成曲線;最后由ASKIN功能生成葉片實際的三維曲面，其包括主、副腹板及最大弦長處橫向加強板。

葉片空間三維坐標變化關系如下

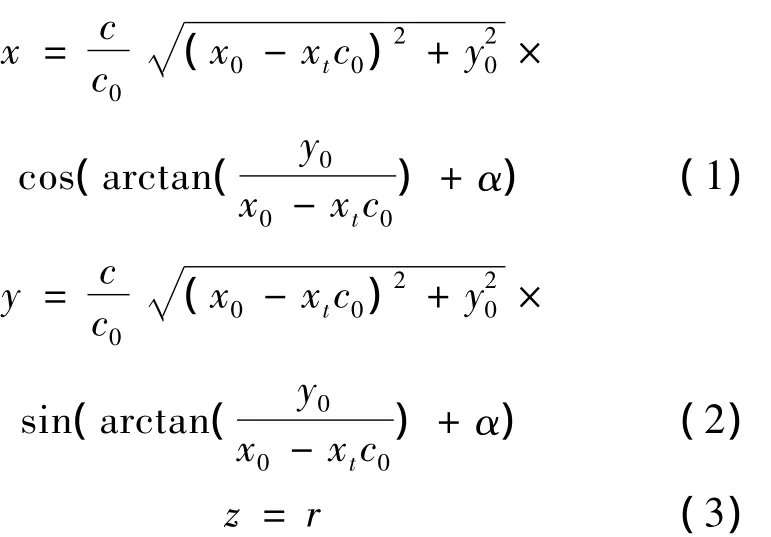
式中:(x0，y0)為二維翼型坐標，(x，y，z)為實際翼型坐標，c0為二維翼型弦長，c為當地弦長，xt為翼型在葉片上旋轉中心至前緣距離，α為當地扭角。

850 kW葉片的弦長、扭角分布如圖3。

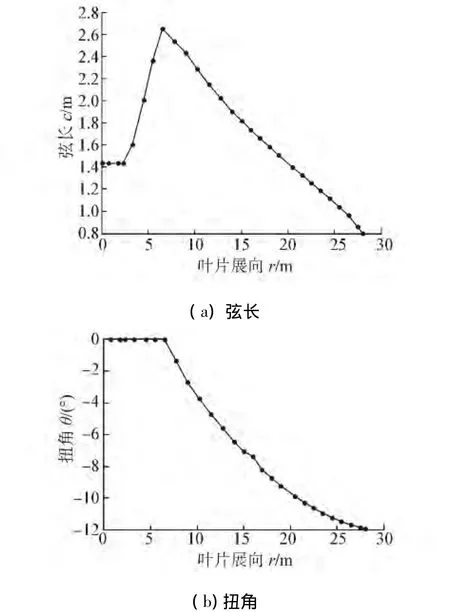
圖3 葉片參數分布Fig.3 Parameter distributions of blade

由此建立風力機葉片殼層結構。考慮有限應變殼單元shell181，其支持所有的非線性功能(包括大應變)，允許有多達250層的材料層，故而采用其進行模擬［11］。再根據前文所述的材料屬性及葉片鋪層狀況，采用四邊形映射網格的方式，對葉片各處進行鋪層及網格劃分，圖4顯示最大弦長處截面細節，其能形象地反映鋪層后葉片內部結構。

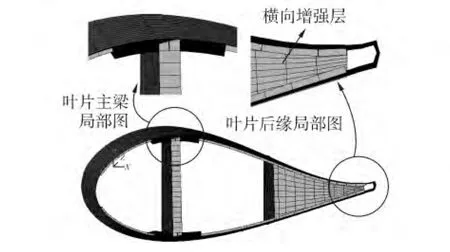
圖4 典型葉片截面細節Fig.4 Section detail of typical blade

3 載荷分析

作用在葉輪上的空氣動力是風力機最主要的動力來源，也是造成各個零部件主要的載荷來源。此外，風力機葉片在風機工作中還受到慣性力、重力、離心力和陀螺力等。針對該鋪層改進的葉片，在二類風區下工作，根據德國GL2010及風力機極限工況的描述，找出其中的危險工況，通過以葉素-動量理論為基礎的BLADED計算得到葉片截面的最大彎矩［12］，如圖5。在施加載荷時，采用在截面之間施加彎矩增量，以避免在各截面直接施加集中載荷而引起與實際不符的過大局部應力。

最后將葉根處自由度約束，如此便完成了整個葉片的約束和加載。經初步計算得到葉片質量為3 992.9 kg，而該葉片實驗測試結果為 4 031 kg，計算與實驗結果誤差不超過1%，即驗證了采用MATLAB和ANSYS聯合編程建立的葉片有限元模型是非常可靠的，也為后續葉片結構的優化奠定了良好的基礎。

圖5 彎矩分布Fig.5 The distribution of bending moment

4 葉片優化模型的建立

4.1 優化目標

針對此葉片，不考慮其制造成本，葉片質量越小，材料成本也會越低。同時在滿足強度、剛度等要求下，葉片的質量越小，其表現出來的疲勞壽命也就越高。因此，本文提出以整個葉片質量最小建立優化目標函數:

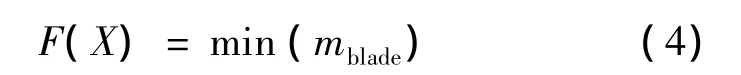
式中:mblade為葉片質量。

4.2 設計變量

本文提出以材料(單向布、雙向布、三向布、膠衣布、泡沫)厚度作為設計變量，并結合葉片實際結構，其腹板位置、主梁寬度及前、后緣加強寬度作為設計變量:

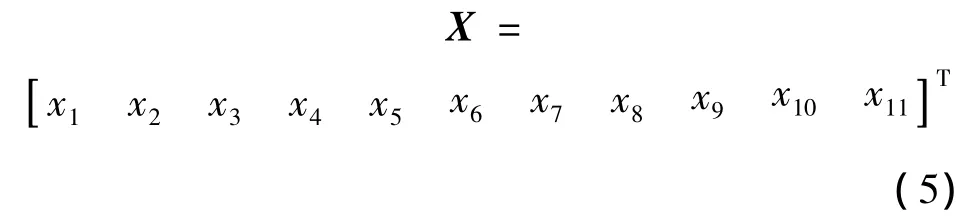
式中:各變量的初始及波動比例見表2、3。

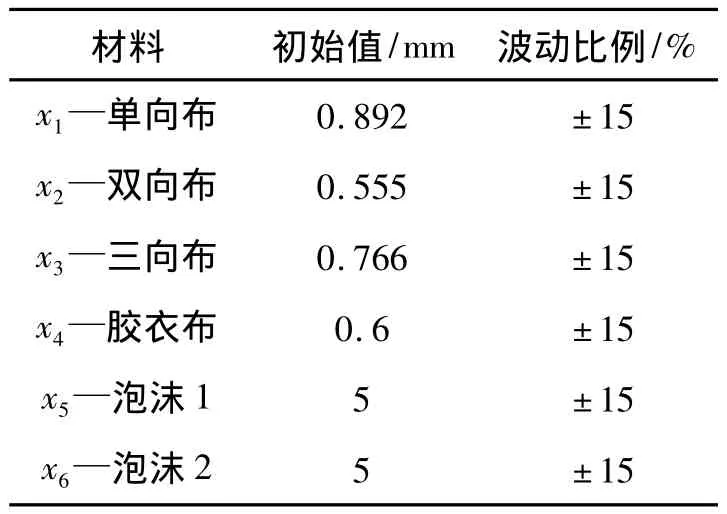
表2 材料厚度Table 2 Thickness of material

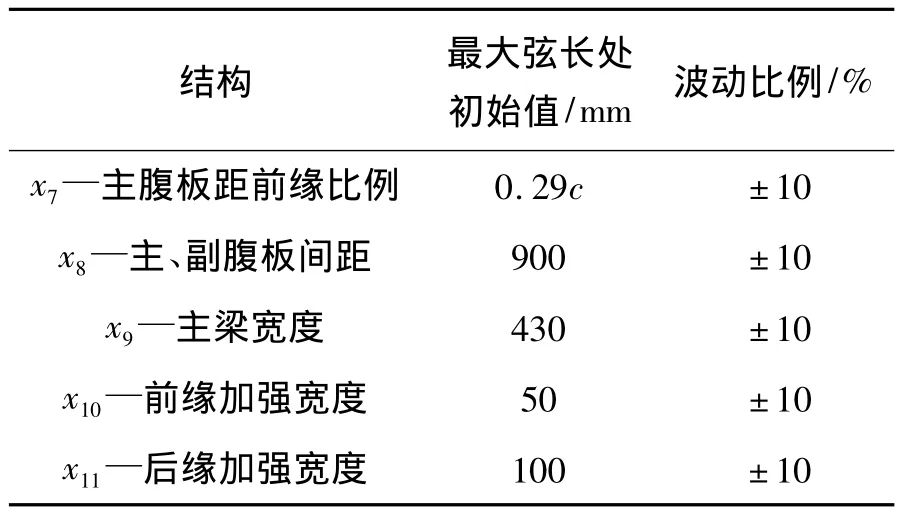
表3 結構尺寸Table 3 Measurement of structure

4.3 約束條件

在風力機正常運行中，為防止其突然破壞，其強度是首先需要考慮的因素。由于風機葉片采用復合材料，其力學性能表現為各向異性，參考相關書籍，本文中以蔡-胡(Tsai-Wu)理論［13］作為強度約束條件，其具體準則如下:

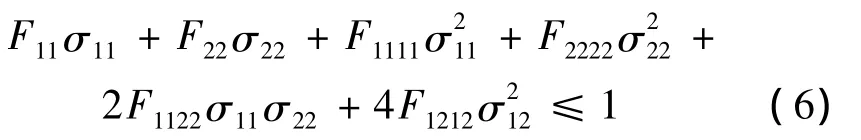
式中:σ11為材料x方向正應力，σ22為y方向正應力，σ12為x-y平面剪切應力，F11、F22、F1111、F2222、F1122、F1212參考蔡-胡理論定義。

風機主要被設計為迎風型，葉片在受載時發生彎曲變形，很容易發生撞擊塔架的事故，因此葉片必須有較強大剛度，即葉片在運行中葉尖位移也是需要考慮的因素。針對此風機正常運轉，其葉片總長28 m，俯仰角為6°，葉根到輪轂中心的距離為2 m，輪轂中心到塔架的距離為2 m，那么葉片未變形時葉尖與塔架的距離為

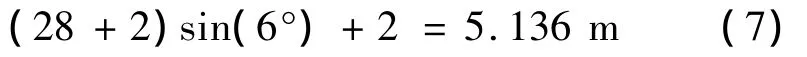
考慮葉尖最大變形量不超過葉片未變形下葉尖與塔架距離70%的限制，即葉尖位移約束條件為

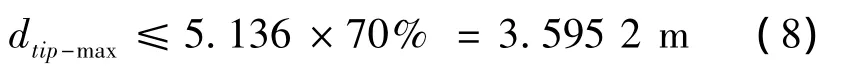
整個葉片的數學優化模型得以建立。本文通過編寫MATLAB程序，結合改進的粒子群的算法進行尋優，從而快速準確地求得其在變量范圍內的全局最優解。

4.4 算法描述

改進的粒子群算法［14］中相關參數需要優先設置，具體如下:

1)慣性權重w是保持原來速度的系數，采用線性遞減策略取值，其表達式為

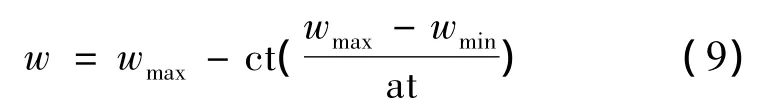
式中:wmax和wmin為慣性權重的最大和最小值，根據規律此處取0.95和0.4，ct為當前迭代次數，at為總迭代次數，此處取50。

2)“認知”c1是粒子跟蹤自己歷史最優值得權重系數，它表示粒子自身的認識，此處采用非對稱反余弦取值，其表達式為

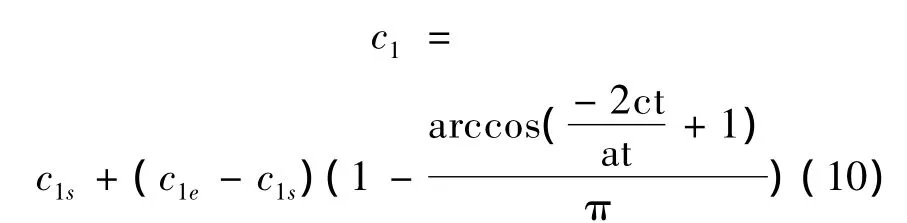
式中:c1s和c1e為c1取的初始值和結束值，此處取2.75和 1.25。

3)“社會”c2是粒子跟蹤群體最優值得權重系數，它表示粒子對整個群體知識的認識，其也采用非對稱反余弦取值，表達式為

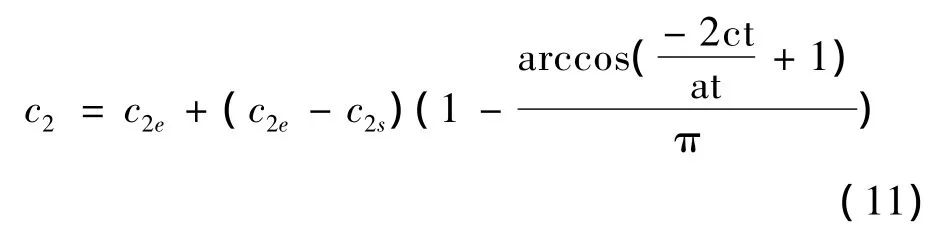
式中:c2s和c2e為c2取的初始值和結束值，此處取0.5 和2.25。

4)粒子維數即變量數，此處取11。

5)種群大小即初始粒子數，此處取30。

5 結果分析

基于上述優化方案，在滿足蔡-胡理論和葉尖位移約束的條件下，其迭代結果如圖6，表明在迭代至40次左右時，優化已達收斂，其具體結果與初始值相比如表4。

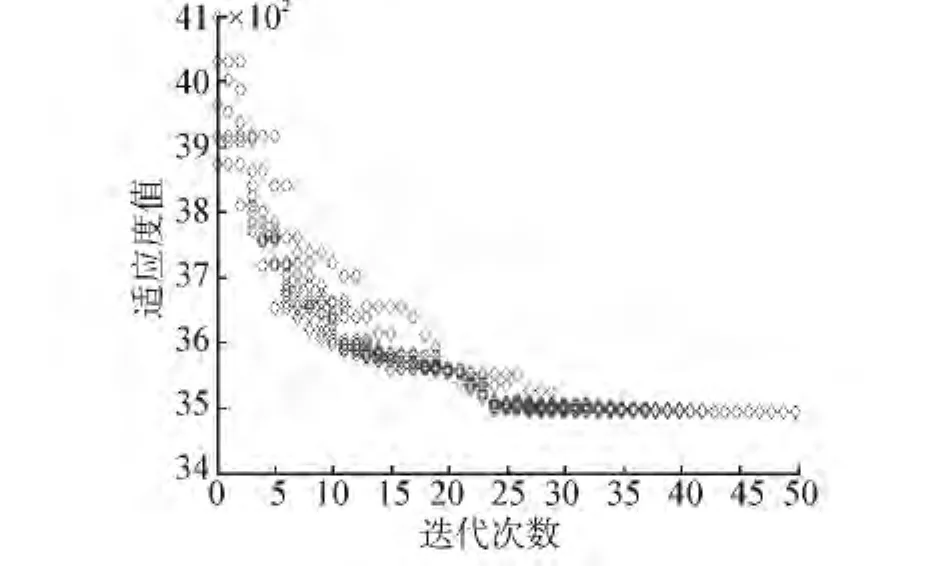
圖6 迭代歷程圖Fig.6 Interative process diagram

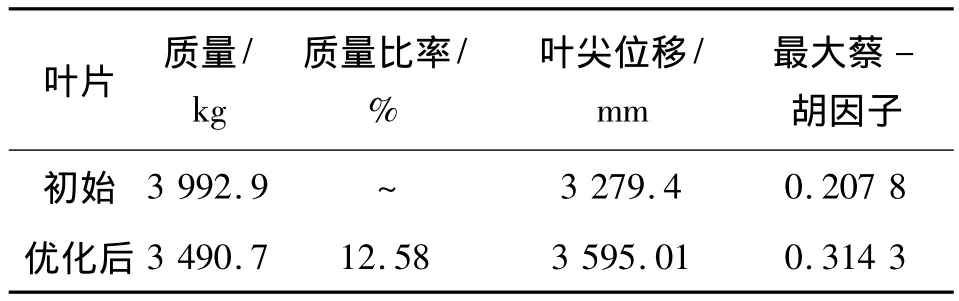
表4 優化結果比較Table 4 Comparison of the optimized results

表4顯示，優化后葉片葉尖位移小于許用值3 595.2 mm，由最大蔡-胡因子可知，葉片的強度也滿足要求，故在滿足約束的條件下優化葉片質量明顯下降。進一步分析，表5給出優化前后各變量具體情況，圖7表示優化后葉片各處厚度及結構尺寸相對初始的變化。其表明，在滿足約束條件的基礎上，所有材料厚度均得到減小，從而降低了葉片質量;而增加主腹板至前緣距離和主梁寬度，減少主、副腹板間距將有利于減小葉尖位移，即能最大限度的減少材料厚度，從而進一步達到降低葉片質量的目的。

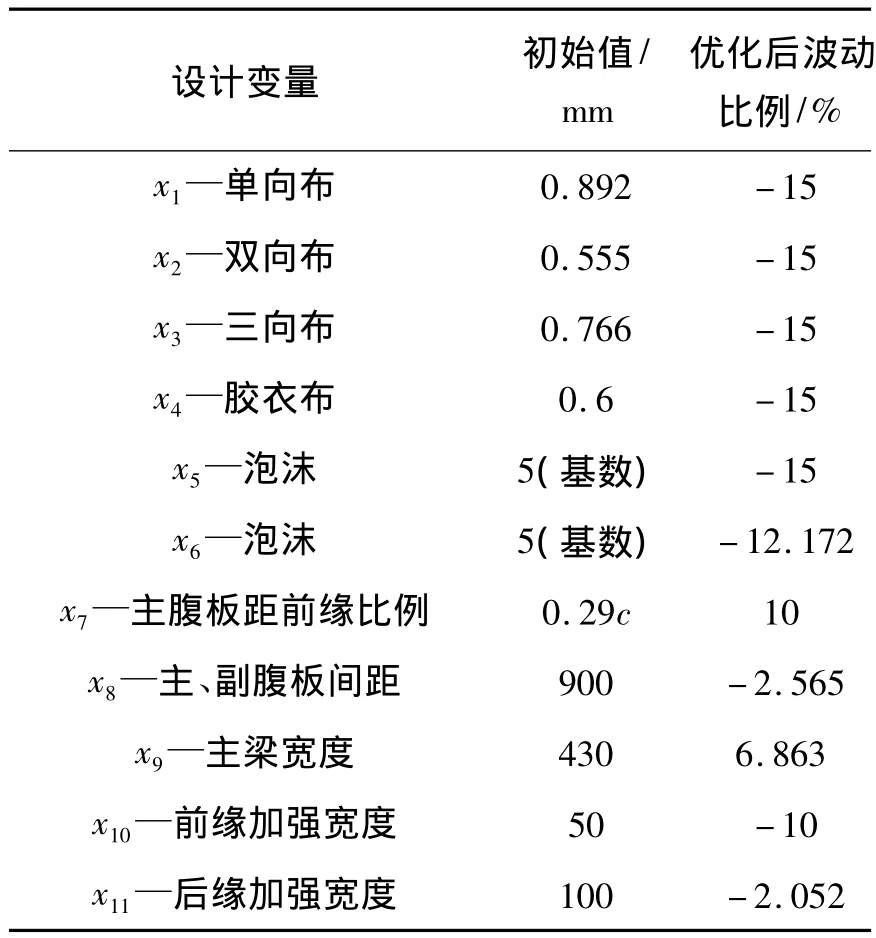
表5 優化變量結果Table 5 Results of optimized variable

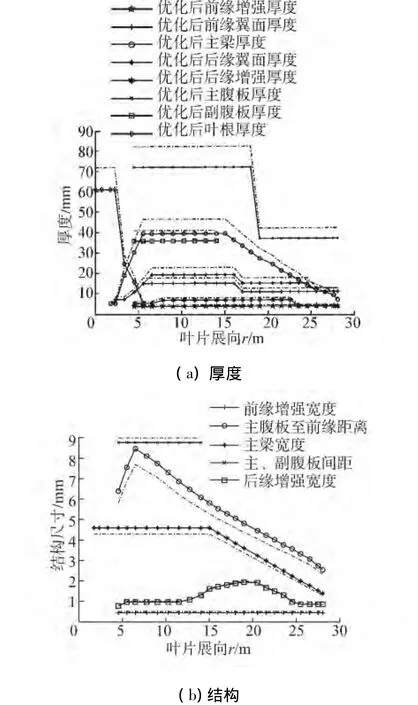
圖7 優化前后比較Fig.7 Comparison before and after optimization of the initial balde

圖8 優化后葉片揮舞方向位移和徑向應變Fig.8 Displacement of wave direction and strain of radial direction about the optimized blade

圖8分別顯示了優化后葉片揮舞方向位移和徑向應變，前者表明葉片最大位移出現在葉尖處，大小為3 595.08 mm;后者表明葉片在受載時，背風面受壓相比迎風面受拉更為嚴重，最大壓應變達到最大拉應變的1.706倍，且其出現在最大弦長附近，這與葉片實際開始破壞的部位完全吻合，因此在考慮葉片材料時需更多的關注材料壓縮的強度。

6 結論

1)基于MATLAB和ANSYS建立復雜葉片的參數化有限元模型，該模型的建立為葉片結構優化提供可能。

2)運用BLADED軟件計算得到葉片各截面處極限載荷，通過分段加載以避免傳統施加集中載荷的缺點;初步計算得到葉片質量，其與實驗結果比較誤差不超過1%，從而驗證模型建立的正確性。

3)以材料厚度及結構參數作為優化變量，葉片質量作為優化目標，建立葉片優化模型，結合改進的粒子群算法進行尋優。經優化表明，在滿足強度和剛度的前提下，優化后的葉片質量降低了12.58%。

［1］MANWELL J F，MCGOWAN J G，ROGERS A L.Wind energy explained theory design and application［M］.Chichester:John Wiley＆ Sons Ltd，2002:274-314.

［2］費金凡.復合材料風力葉片結構的有限元分析［D］.武漢:武漢理工大學，2009:3-5.FEI Jinfan.Structural ANSYS of composite wind blade using finite element method［D］.Wuhan:Wuhan University of Technology，2009:3-5.

［3］KONG C，BANG J，SUGIYAMA Y.Structural investigation of composite wind turbine blade considering various load cases and fatigue life［J］.Energy，2005，30:2101-2114.

［4］LUND E，STEGMANN J.On structural optimization of composite shell structures using a discrete constitutive parameterization［J］.Wind Energy，2005，8:109-124.

［5］LIAO C C，ZHAO X L，XU J Z.Blade layers optimization of wind turbines using FAST and improved PSO algorithm［J］.Renewable Energy，2011，2:1-7.

［6］CHEN Jin，WANG Quan，SHEN Wenzhong.Structural optimization study of composite wind trubine blade［J］.Material＆ Design，2013，46:247-255.

［7］王鋒，陳坤.CGI56-850kW 聚酯葉片設計與強度分析［R］.綿陽:中國空氣動力研究與發展中心計算空氣動力研究所，2011:1-35.WANG Feng，CHEN Kun.Design and strength analysis of cgi56-850kw wind blade［R］.Mianyang:Computational Aerodynamics Research Institute of Chinese Aerodynamics Research and Development Center，2011:1-35.

［8］LOCKE J，VALENCIA U.Design studies for twist-coupled wind turbineblades［R］. SandiaTechnicalReport:SAND2004-0522.2004.

［9］張禮達，任臘春.風力機葉片外形設計及三維實體建模研究［J］.太陽能學報，2008，29(9):1177-1180.ZHANG Lida，REN Lachun.Shape design and 3d modeling study for blades of wind turbine［J］.Acta Energiae Solaris Sinica，2008，29(9):1177-1180.

［10］南時雨，劉旺玉.基于APDL的風力機葉片CAD/CAE一體化建模技術［J］.機電工程技術，2007，36(4):76-78.NAN Shiyu，LIU Wangyu.An integrated CAD/CAE modeling technique for wind turbine blade based on APDL［J］.Mechanical and Electrical Engineering，2007，36(4):76-78.

［11］費金凡，張小玉，李卓球.風力機葉片CAD與CAE結合建模計算［J］.固體力學學報，2008，29:38-40.FEI Jinfan，ZHANG Xiaoyu，LI Zhuoqiu.Modeling and calculation of wind turbine blade using CAD and CAE［J］.Chinese Journal of Solid Mechanics，2008，29:38-40.

［12］周鵬展，曾竟成，肖加余.基于BLADED軟件的大型風力機葉片氣動分析［J］.中南大學報，2010，41(5):2022-2027.ZHOU Pengzhan，ZENG Jingcheng，XIAO Jiayu.Aerodynamic analysis of a large-scale wind turbine blade based on BLADED software［J］.Journal of Central South University，2010，41(5):2022-2027.

［13］劉新東，劉偉.復合材料力學基礎［M］.西安:西北工業大學出版社，2010:155-160.LIU Xindong，LIU Wei.Compound material mechanics［M］.Xi＇an:Northwestern Polytechnical University Press，2010:155-160.

［14］李麗，牛奔.粒子群優化算法［M］.北京:冶金工業出版社，2009:35-37，61-63.LI Li，NIU Ben.Particle swarm optimization［M］.Beijing:Metallurgical Industry Press，2009:35-37，61-63.