用虛位移原理處理復雜的平衡問題

(南京師范大學附屬中學江寧分校，江蘇 南京 211102)

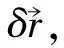
虛位移原理最早由瑞士著名數學家約翰·伯努利(Johann Bernoulli,1667-1748)在1717年提出,又叫做虛功原理(principle of virtual work),是力學中的一條重要原理.虛位移原理的有意思之處在于其給出了求解靜力學平衡問題的動力學方法.讓我們來看一個具體的問題.

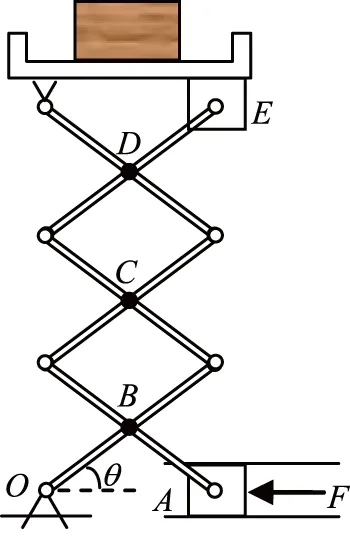
圖1

如圖1所示為升降機的結構示意圖,已知桿長為l,桿與桿間用鉸鏈連結,物塊的重力為mg.與A相連的物塊可在軌道中滑動,與E相連的物塊可在與其接觸的面上滑動,不計桿的質量和一切摩擦.求使系統平衡的外力F.

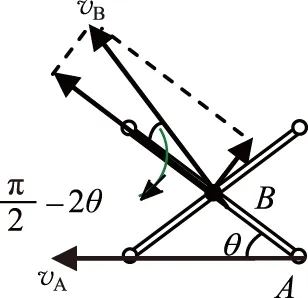
圖2

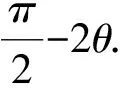
因為沿桿的速度相等，所以有:

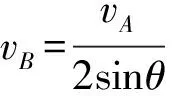
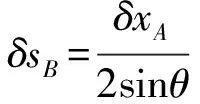
(1)

又因為B點的位移中y方向上的分量為:δyB=δsB·cosθ

(2)

再考慮到方向,由(1)(2)兩式可得:

(3)

不難發現，C點相對B點的位移為2δyB，D點相對于C點的位移也為2δyB、E點相對于D點的位移為δyB，所以，E點相對于地面的位移為6δyB，由虛位移原理，有：

δW=FδxA+mg·6δyB

(4)

由(3)(4)兩式可得F=3mgcotθ

從以上解答過程可以看出,應用虛位移原理時,首先要假設一個虛運動,然后再找出相關虛位移之間的關系,最后利用虛位移原理列方程求解.當然,上述問題也可以用力的平衡和力矩的平衡知識來解,但是會比較繁瑣.

實際上,對于受理想約束(即沒有摩擦且約束力做功等于零的約束)的復雜系統的平衡問題,因為虛位移原理直接給出了各主動力之間的關系,從而使公式中避免出現約束力,這就避免了解聯立方程,使得計算過程大為簡化.

在處理復雜的平衡問題時,虛位移原理會顯得特別有力.另外,虛位移原理不僅可以用來求主動力,還可以功妙地求出系統的內力.下面讓我們來看一個復雜的求內力的問題.

如圖所示,一桁架尺寸和所受荷載如圖所示.已知:l=5m,h=3m,F=100N,假設各桿之間用鉸鏈相連,G點用一個可以左右滑動的架子支撐.試求CD桿中的內力(不計桿的質量和一切摩擦).

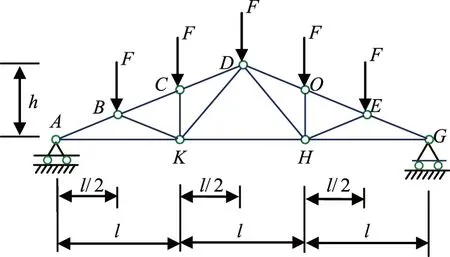
圖3

對于這個問題,如果單純用力的平衡和力矩的平衡來處理,確實不太容易理出思路,而如果采用虛位移原理,則會簡明許多.

我們可以將桁架的CD桿截斷，如圖所示，以F1和F1′代之，這樣桁架就分成了由桿AB、BC、CK、AK、BK組成的剛體Ⅰ和由桿DO、OE、EG、GH、HK、KD、DH、HO、HE組成的剛體Ⅱ.

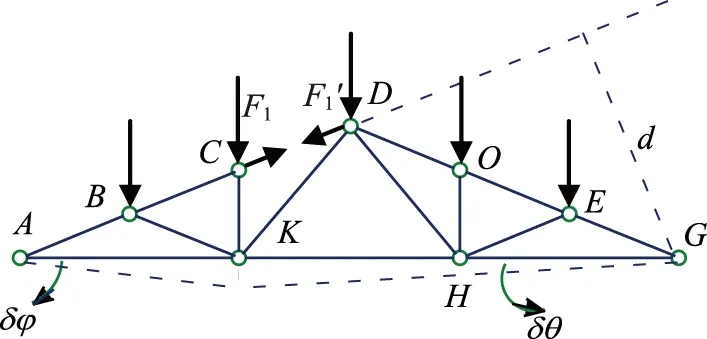
圖4

假設K點向下有一個虛位移,設d為G點到F1′的作用線的垂直距離,此時剛體Ⅰ繞A點轉過的角度為δφ,剛體Ⅱ繞G點轉過的角度為δθ,此時F1與其作用點的位移垂直,不做功,F1′的功F1′dδθ,由虛位移原理,可得:

(1)

桁架下方的三根桿的彈力與虛位移方向垂直,所以不考慮其做功,所以

(2)

又顯然有:lδφ=2lδθ

(3)

由(1),(2),(3)式可得:

負號表示和圖示方向相反,桿CD中的彈力為壓力.

剛體是不可以發生形變的，題中原來的各個構件之間是不可以有相對運動的,這里我們巧妙地截斷了CD桿,假設了一個運動,這樣虛位移原理得以運用.

綜上所述,虛位移原理對于復雜的靜力學問題,是一個特別簡明有力的方法,另外,雖然虛位移原理給出的是質點或系統外力(主動力)之間的關系,但也可以通過巧妙的處理,來求出系統的內力.