小波Contourlet變換圖像壓縮算法
田 馳
(鐵嶺師范高等專科學校, 遼寧 鐵嶺 112000)
小波Contourlet變換圖像壓縮算法
田 馳
(鐵嶺師范高等專科學校, 遼寧 鐵嶺 112000)
為改進Contourlet變換冗余大的缺點,提出了一種小波Contourlet變換的圖像壓縮優化算法。實驗結果表明,在高壓縮率下算法具有優勢。
小波; Contourlet變換; 圖像壓縮
0 引 言
現階段主流的圖像壓縮方法一般都采用變換、量化以及熵編碼的基本框架。利用具備能量集中性的變換能夠在利用很少的向量的條件下較為有效地逼近某一類信號。當前小波變換在非平穩信號處理中得到了越來越廣泛的應用和普及,并表現出了巨大的優越性。但是圖像作為一種特殊的二維信號,其本身存在著諸多特點,在不少情況下,可分離的小波變換無法對圖像取得較高的表示效率[1-2]。基于此,文中對小波Contourlet變換的圖像壓縮算法進行了探討。
1 小波Contourlet 變換
可以將Contourlet 變換劃分成兩個階段:第一個階段是通過拉普拉斯金字塔來對圖像做多尺度分解處理,目的在于捕獲奇異點。第二個階段是利用方向濾波器組把各自分布在同方向上的諸多奇異點合成一個系數。拉普拉斯金字塔分解只對低頻部分來采取下采樣,經過處理后數據會形成冗余。與此同時,小波Contourlet 變換中會通過二維小波變換來取代拉普拉斯金字塔進行子帶分解處理[3]。考慮到小波分解以及方向濾波器組都屬于無冗余的,所以小波Contourlet 變換實際上也不會出現冗余問題。
實際應用中,可以將小波Contourlet 變換劃分成兩部分:一是通過小波變換來實施子帶分解,然后還應當在每一級變換取得高頻子帶HH,HL以及LH;二是通過方向濾波器組對其同級的高頻子帶來實施相同級數的方向分解處理[4]。一般來說,應當從最高頻子帶開始方向濾波,其級數用L表示,那么其每個子帶均可以被分解為ND=2L塊。

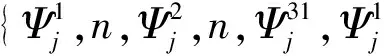
m,i=1,2,3
2 圖像編碼算法
2.1線性索引
文中在無鏈表算法中通過線性坐標索引映射來將原來的二維的小波Contourlet變換系數轉為一維的索引值,利用這種方法可以快速地得到集合以及像素的具體位置。其中系數的索引號可以通過單個數字來進行表示[5]。需要指出的是,這樣的索引映射下每個大小為2×2 塊中的4 個系數索引值均能夠保持連續性,同時,根據引遞增的形式編碼也是符合SPECK編碼的正常掃描順序的。
2.2狀態標記情況
文中采用的算法一共提供了5種狀態標記來對于小波Contourlet變換下所處的編碼狀態進行記錄和分析。其中,MIP主要負責記錄比特面的不重要像素以及未測試相關像素;MSP主要負責記錄的是重要的,同時需要細化的相關像素;MNP主要負責記錄新的重要同時比特面不必進行細化的相關像素;MSn 主要負責對2n×2n的集合塊進行記錄,一旦發現某個像素的狀態用n來表示,就意味著以該像素的索引值來當做起始的數量是2n×2n大小的像素當做一個集合來實施重要性編碼。Mik主要負責對于剩余集合I的表示,符號意義上,k代表的是系數子帶的級數,I 每分裂一次,則用k+1來進行表示。
需要注意的是,狀態標記過程中應當注意以下幾點內容:首先初始化分裂次數,并且狀態標記位數。注意應當用MIP來表示全部的狀態表元素[6]。選擇LL0來當做初始集合塊S,注意對于第一個元素應當通過MSn來進行表示。剩余元素通過集合I來表示,而第一個元素則可以使用Mik來進行表示。然后再根據索引值的順序來實施掃描處理,對于任何一個單個元素,都應當注意對其重要性做出準確的判斷,進行編碼符號位處理同時還要把元素的狀態位置用MNP來進行表示;如果不重要,則可以繼續對下一個元素來進行掃描[7-8]。
同樣的,還需要對集合S重要性來做出判斷,判定為重要則集合應當做四叉樹分解處理,同時還應把得到的四個子集的首個元素的狀態位置標記成n- 1。反之,假若其不重要則應當跳過,然后對其它元素來進行掃描。在對于集合I的重要性判斷的過程中,假若得出其重要,則應當將其分裂為3 個S 集合以及1 個I集合,其中對于S 集合的第一個元素狀態位置可以通過MSn來進行表示,而對于I 集合的第一個元素狀態位置則可以用Mik+1來進行表示。
2.3CLSK算法
文中采用了CLSK算法,根據線性索引的順序由高位平面逐漸至低位平面來實施編碼處理,需要注意的是,對集合和像素重要性的判斷標準可以用下式來進行界定:
符號意義上,Sn(t)=1代表的含義是塊非常重要,而Sn(t)=0代表的含義是塊t不重要。我們利用Mark[t]來對于系數索引值為t的狀態的標記位來進行表示。那么具體對圖像實施CLSK編碼應當通過以下幾個步驟來完成:
1)首先應當確定初始閾值為n=2[log2mzxc(i,j)],同時初始化狀態標志。
2)通過集合x來對于分解后的子帶來進行表示,需要注意的是低頻子帶系數構成的是集合S,而剩下的其它小波子帶則用集合I來進行表示。
3)做好排序過程,具體實施是應當由索引值t=0開始來進行逐步的掃描。掃描分為4種情況:第一,假若Mark[t]=MIP,那么就應當輸出Sn(t)。假若Sn(t)的值為1,那么就需要輸出系數Ct的符號,用公式表示就是Mark[t]=MNP,t=t+1。第二種情況是,假若Mark[t]=MNk,那么就輸出Sn(t)。假若Sn(t)的值等于1,就需要采取集合分裂。第三種情況是,假若Mark[t]=Mik,那么就會輸出Sn(t)。如果Sn(t)的值為1,就會分解成3 個S集合以及新集合I。第四種情況是:t=t+1。
4)注重細化過程,同時開始對索引值進行重新掃描。假若Mark[t]=MSP,這種情況下就會輸出Ct的第n層bit,反之假若Mark[t]=MNP,那么就需要令Mark[t]=MSP;t=t+1。
5)最后要進行循環更新量化門限,注意對n減1。完成之后再轉到步驟3)。
3 實證分析
為了對于本研究中提出的編碼算法的有效性進行驗證,采用512×512×8 bit 大小的圖像Goldhill以及Barbara 作為研究對象來開展性能測試實驗,同時將實驗結果和基于小波的圖像編碼算法SPIHT來進行比較。本試驗中,選擇了9/7 雙正交提升小波為實驗對象,并將其分解層次為四級。具體的不同壓縮率下算法解碼圖像的峰值信噪比情況見表1。
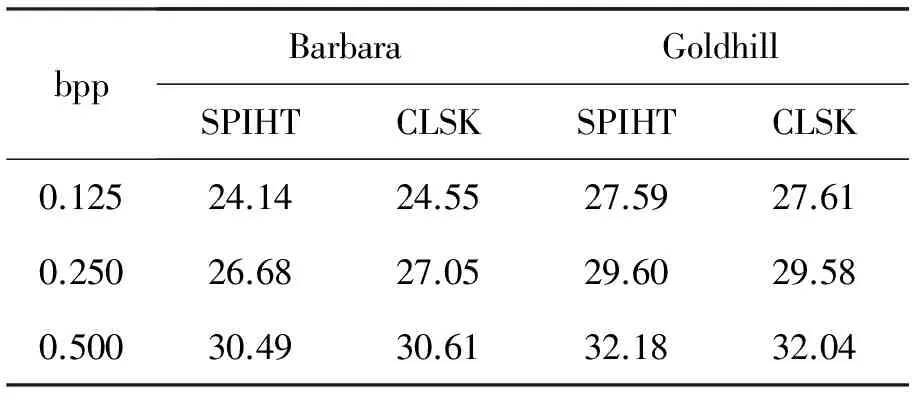
表1 重構圖像的峰值信噪比情況比較
從表中不難看出,CLSK算法和SPIHT算法處于不同碼率情況下, Barbara 以及Goldhill 的重構圖像在峰值信噪比比較上是較為相近的。一是由于CLSK 算法使用的是狀態標記取代鏈表方式,因而編碼過程中未能夠采用集合大小的重新排序過程,從而導致了編碼效率降低。二是受到對紋理更豐富的圖像Barbara的影響,采取方向濾波后可以獲得對圖像的更“稀疏”的標記,對于圖像壓縮具有一定的積極意義,因而其峰值信噪比略高。Barbara 在0.2bpp條件下通過小波變換的SPIHT與CLSK 算法所得到的重構圖像如圖1所示。

(a) SPIHT

(b) CLSK
從圖中不難看出,在相同碼率的條件下,后者更多的保留了圖像的邊緣和圖像紋理等諸多細節信息,和小波變換算法所獲得的主觀視覺效果相比,具有較大優勢。
4 結 語
綜上所述,本研究中對于Contourlet變換冗余大的弊端進行了改進,提出了基于Contourlet變換的新型無鏈表CLSK 算法編碼算法,仿真結果表明,在高壓縮率下,該算法能夠取得較為理想的效果。
[1] 薛旭成,張淑艷,李洪法,等.Contourlet變換在圖像壓縮中的應用研究[J].微計算機信息,2009(9):154-158.
[2] 楊粵濤.基于非采樣Contourlet變換的圖像融合[D]:[碩士學位論文].長春:長春光學精密機械與物理研究所,2012.
[3] 李杏梅.Contourlet變換在圖像去噪與邊緣檢測中的應用研究[D]:[碩士學位論文].武漢:華中科技大學,2011.
[4] Eslami R, Radha H. New image tr ansform using hybrid wav elets and dir ect ional filter banks:analysis and design[C]// MPro ceeding of IEEE Inter national Conference on Image Processing. Piscateway,USA:IEEE,2005.
[5] Latte M V, Ay achit N H. Reduced memory listless speck image compression[J]. Digital Signal Processing,2006(6):245-250 .
[6] 宋宇,王美玲,翟雙.基于小波變換的圖像壓縮算法[J].長春工業大學學報:自然科學版,2011,32(6):558-561.
[7] 杜廣環.基于小波變換圖像壓縮編碼研究的現狀與發展[J].科技創新導報,2011,31(10):87-89.
[8] 譚艷梅.一種基于小波變換的圖像壓縮方法與實現[J].微型機與應用,2011,3(17):86-88.
A wavelet transform Contourlet based image compression algorithm
TIAN Chi
(Tieling Normol College, Tieling 112000, China)
To improve the Contourlet transform algorithm, we propose a wavelet transform Contourlet based image compression algorithm which has advantages at high compression rate verified by experiments.
wavelet transform; Contourlet transform; image compression.
2014-03-11
田 馳(1981-),女,漢族,遼寧鞍山人,鐵嶺師范高等專科學校講師,碩士,主要從事計算機圖形圖像處理及應用方向研究,E-mail:zly19800212@163.com.
TP 30
A
1674-1374(2014)04-0442-04

