數值級數法求解薛定諤方程
孫建英, 蹇玲玲, 高發玲
(青島理工大學琴島學院,山東 青島 266106)
0 引 言
在工程領域和物理科學中,大量的現象可以用薛定諤偏微分方程來刻畫,也產生一些求解薛定諤偏微分方程的數值解法[1-7],文中將結合非標準有限差分格式的特點,給出一種計算此類方程的新方法——數值級數法,該方法簡潔、有效、精度高。其特點是可以將每個網格點(xm,tn)處的數值解unm以級數的形式給出
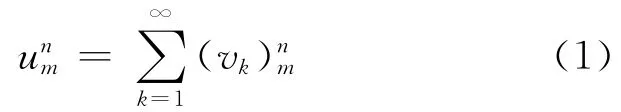
文中考慮如下初邊值一維薛定諤方程:

式中:T,L——非負常數;
φ(x),g0(t),g1(t)——連續函數。
1 差分格式的構造
對式(2)半離散得到差分方程
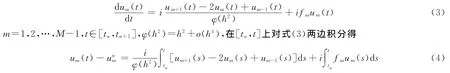
設

則有

則數值解記為
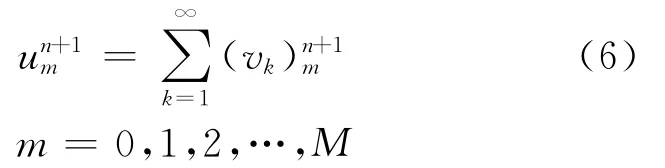
當m=0,m=M時,由邊界條件得:
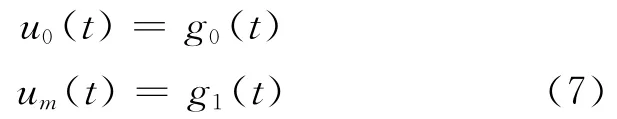
則取

當m=0,1,2,…,M-1時,將式(5)代入式(4)得:
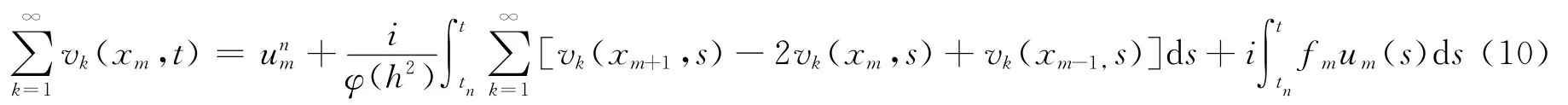
比較上式兩端得到遞推計算公式:
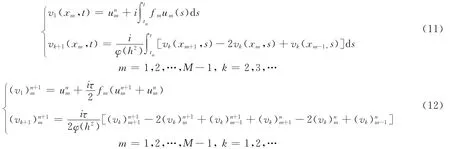
進一步整理得:

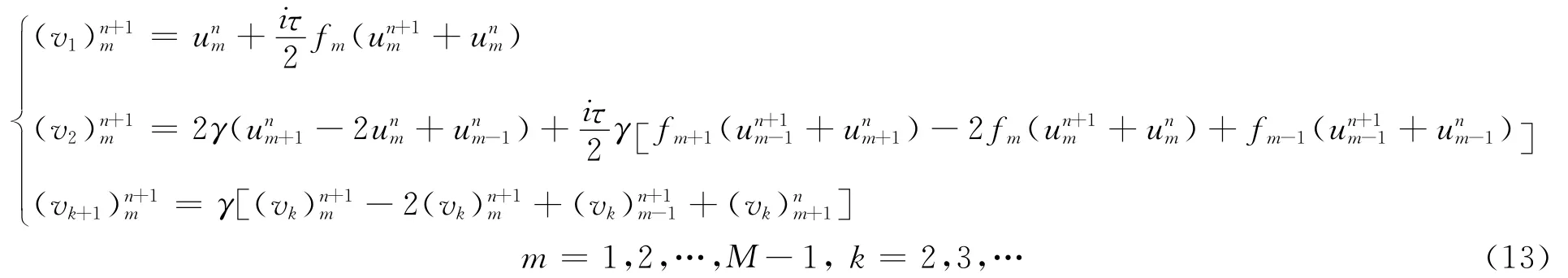
2 收斂性的證明
定理1 差分格式(13)無條件收斂。
3 穩定性的證明
定理2 差分格式(13)無條件穩定。
證明 對式(13)兩端求和得:
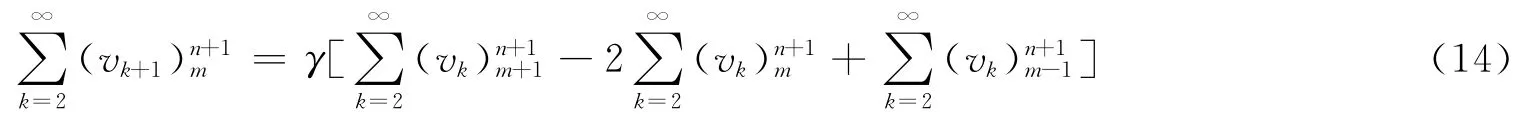
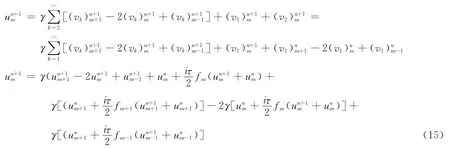
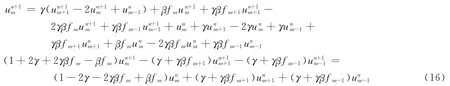
令

所以

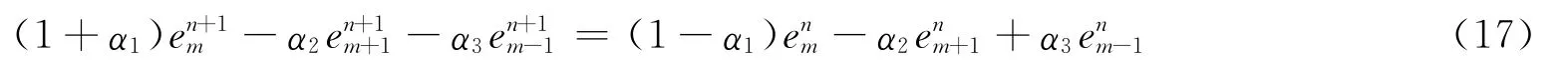
則寫成矩陣方程為:
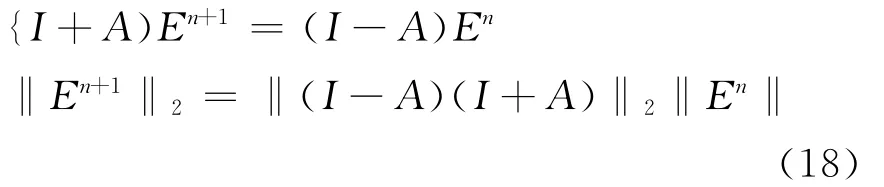
則易得:
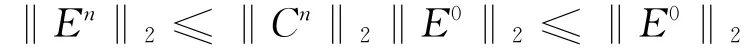
其中:
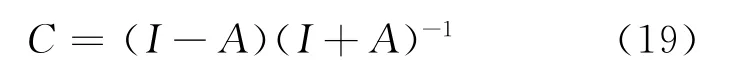
所以差分格式無條件穩定的。
4 數值算例
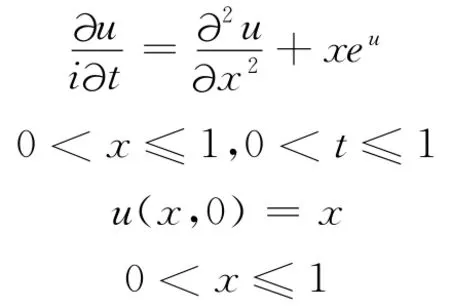
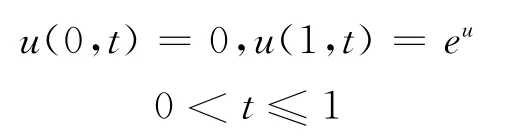
這個問題的精確解為u(x,t)=xeit。取時間步長為0.05,空間步長為0.1,進行數值計算,結果見表1。
從表1可以看出,文中給出的數值解法解決此類問題是一個有效的方法。
[1]張睿,王軍帽,韓家驊.一類非線性薛定諤方程的精確解析解[J].安徽大學學報:自然科學版,2009,33(3):52-55.
[2]曹曉亮,林機.含三階色散項的非線性薛定諤方程的微擾對稱和近似解[J].浙江師范大學學報:自然科學版,2010,33(1):56-62.
[3]李瑩,崔慶豐.基于分布傅里葉變換法對非線性薛定諤方程的數值仿真[J].長春理工大學學報:自然科學版,2011,34(1):43-45.
[4]周鑫,胡先權.球諧環形蕩勢薛定諤方程的精確解[J].重慶師范大學:自然科學版,2011,28(5):63-66.
[5]張彗星,劉文斌.帶有磁勢和臨界增長的薛定諤方程解的存在性[J].吉林大學學報:理學版,2012,50(2):227-231.
[6]李昊辰,孫建強,駱思宇.非線性薛定諤方程的平均向量場方法[J].計算數學,2013,35(1):59-66.
[7]肖氏武,丁凌.具有調和勢和耗散非線性項的薛定諤方程的解的存在性及集中現象[J].西南大學學報:自然科學版,2013,35(10):71-74.
[8]劉明鼎.數值級數法求解一維拋物型方程[J].哈爾濱師范大學學報:自然科學版,2013,29(2):1-4.

