時間序列模型預測流感發病率的研究
陸波 閔紅星 扈學琴 閔佳
時間序列模型預測流感發病率的研究
陸波 閔紅星 扈學琴 閔佳
目的 探討ARIMA模型在流感發病預測方面適用性, 為擴大該模型在傳染病發病預測方面的應用提供科學依據。方法 收集本市醫療機構2004~2009年的流感月發病數資料, 用Eviews6.0軟件ARIMA預測模型, 對模型的適應性進行檢驗驗證其有效。結果 本市流感月發病數時間序列的自相關分析圖顯示數據不平穩, 所以進行一階差分, 并建模, 最終模型為ARIMA(0, 2, 0), 所建模型有統計學意義。說明用ARIMA(0,2,0)模型能夠預測流感。結論 ARIMA模型法對不同疾病的預測效果存在差異,在建模前應考慮時間序列的平穩, 如不平穩通過差分把它變換成平穩的時間序列化, 且建模的數據不能太少, 不能低于50個。
流感;ARIMA模型;預測
時間序列分析方法有指數平滑和ARIMA模型。ARIMA模型利用計算軟件常規運算, 要求時間序列滿足平穩性條件, 且對資料的要求也不高, 是用變量過去的觀測值來預測同一變量的未來值, 適用于任何時間序列發展形態的高級預測方法。
1 資料與方法
1.1 一般資料 本市2004年1月~2008年12月的流感月發病數(60個數據)通過國家疾病報告管理系統進行收集,建立預測模型, 用2008年各月發病數進行組外回代和組內回代, 對2009年流感的發病情況進行預測。
1.2 統計預測方法 用Eviews6.0進行數據處理與分析。
2 結果
2.1 流感流行特征分析 見圖1。
2.2 建立預測模型 ①模型識別 2004~2008年原始時間序列進行一級差分處理, 通過單位根檢驗說明該數據滿足平穩條件, 取ARIMA(0,2,0)模型。見圖2, 圖3。②參數估計和模型檢驗 對ARIMA(0,2,0)的適應性進行檢驗。根據SPSS11.5輸出結果顯示模型所有參數有統計學意義, P>0.05;對殘差序列作自相關函數圖, 顯示殘差序列為白噪聲, 說明所選的ARIMA(0,2,0)模型可以用于預測, 見圖4。③預測應用, 見圖5。
3 討論
3.1 ARIMA模型法在傳染病預測的意義 近年來, 有學者開始探討其在醫學領域的應用, 認為該方法能較好的適用于疾病發病或死亡的預測預報[1]。2003年, 有學者應用這種方法預測SARS的疫情趨勢, 取得了較好的效果[2]。相比之下認為, ARIMA模型是一種精度較高的短期預測模型[3], 此模型本研究應用ARIMA模型法預測傳染病, 是用預測疾病的過去值和現在值, 預測未來值, 參照預測數據有目的地開展傳染病的防控工作。
3.2 ARIMA模型法可以用于流感發病的預測 根據本市2004~2008年各月份的流感發病數序列的時序圖發現:流感月發病數呈現明顯波動, 每年12月或次年1月為發病高峰月,有相對固定的季節性或周期性波動。但2006年12月和2007年1月流感樣病例數出現2次高峰, 是由于這一時期銀川市發生2次學校流感暴發疫情引起。對AR(1)模型進行一級差分處理和單位根檢驗, 使數據滿足平穩條件, 將模型優化為ARIMA(0,2,0)模型建模, 并對ARIMA(0,2,0)的適應性進行檢驗, 顯示殘差序列為白噪聲, 說明所選的ARIMA(0,2,0)模型是合適的, 可用來預測, 用Eviews6.0擬合模型, 得到的五年預測效果的擬合優度R2為0.258, 相關系數為0.5079。因此,所選的ARIMA(0,2,0)所建模型, 有統計學意義。

圖1 銀川市2004~2008年流感月發病數時序圖

圖2 2004~2008年流感發病原始數據的自相關圖、偏相關圖及統計量

圖3 2004-2008年流感發病一級差分后的自相關圖、偏相關圖及統計量
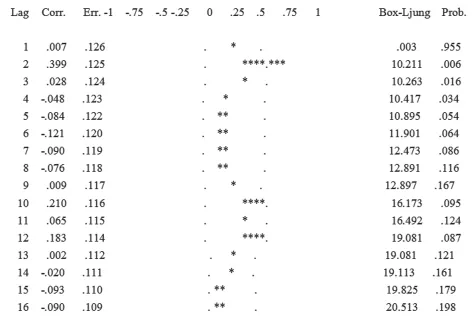
圖4 2004~2008年流感殘差自相關檢驗結果

圖5 2004~2008年流感實際發病數與預測發病數
[1] 鐘朝暉,劉達偉,張燕.重慶市主城區入口死亡率的時間序列分析.中國公共衛生, 2003, 19(7):796-799.
[2] 方兆本,李紅星,楊見萍.基于公開數據SARS流行規律的建模及預報.數理統計與管理, 2003, 22(5):48-52.
[3] 邢慧嫻,楊維中,王漢章.傳染病預測.預防醫學情報雜志, 2006, 6(4):639-642.
750004 寧夏醫科大學總醫院
閔紅星

